4.ボールも箱も区別しない場合
$ここではm個のボールをn個の箱に入れる(n組に分ける)ことを$
$\hspace{1em} (m_1,m_2,\cdots , m_n) と表すことにします。ただし m_1 \leqq m_2 \leqq \cdots \leqq m_n とする。$
$例1 4個のボールを3つの箱に入れる(3組に分ける)場合$
$全事象は (0,0,4),\ (0,1,3),\ (0,2,2),\ (1,1,2)の4通りであるが、どれが起こることも同様に$
$確からしいとして$
$\hspace{2em} P(4,3)=\cfrac{1}{4}$
$例2 7個のボールを3つの箱に入れる(3組に分ける)場合$
$全事象は (0,0,7),\ (0,1,6),\ (0,2,5),\ (0,3,4)\ (1,1,5),\ (1,2,4),\ (1,3,3),\ (2,2,3)$
$の8通りであるが、どれが起こることも同様に確からしいとして$
$\hspace{2em} P(7,3)=\cfrac{4}{8}=\cfrac{1}{2}$
$例3 6個のボールを4つの箱に入れる(4組に分ける)場合$
$全事象は (0,0,0,6),\ (0,0,1,5),\ (0,0,2,4),\ (0,0,3,3),\ (0,1,1,4),\ (0,1,2,3),\ (0,2,2,2),\ (1,1,1,3),\ (1,1,2,2)$
$の9通りであるが、どれが起こることも同様に確からしいとして$
$\hspace{2em} P(6,4)=\cfrac{2}{9}$
$一般に、m個のボールをn個の箱に入れる(n組に分ける)場合、どの箱(組)にも$
$少なくとも1個入るような分け方の総数をf(m,n)で表すことにします。$
$上の例では、f(4,3)=1,\ f(7,3)=4,\ f(6,4)=2 です。$
$このf(m,n)について次の性質が成りたちます。$
$(1)\ f(m,1)=1$
$\hspace{2em} m個のボールを1つの箱に入れる入れ方は1通り$
$(2)\ m < n のとき f(m,n)=0$
$\hspace{2em} ボールの個数より箱の個数が多ければ、空き箱ができる。$
$(3)\ f(m,m)=1$
$\hspace{2em} ボールの個数と箱の個数が等しければ、どの箱にも1個ずつ入る。$
$(4)\ m > n のとき$
$\hspace{2em} n個の箱に初めにボールを1個ずつ入れておくと、残り(m-n)個のボールをn個の箱に入れればよい。$
$\hspace{2em} このとき、ボールが入らない箱があってもよいから次のようなケースに分かれる。$
$\hspace{3em} n 個の箱に入れる(入らない箱は0個)とき f(m-n,n)通り$
$\hspace{3em} (n-1)個の箱に入れる(入らない箱は1個)とき f(m-n,n-1)通り$
$\hspace{3em} (n-2)個の箱に入れる(入らない箱は2個)とき f(m-n,n-2)通り$
$\hspace{5em} \vdots$
$\hspace{3em} 1 個の箱に入れる(入らない箱は(n-1)個)とき f(m-n,1)通り$
$よって、次のような漸化式が導かれます。$
$\qquad m個のボールをn個の箱に入れる場合、どの箱(組)にも少なくとも1個入るような分け方の総数f(m,n)は$
$\hspace{3em} f(m,n)=f(m-n,n)+f(m-n,n-1)+ \cdots + f(m-n,1)$
$例えば$
$f(3,2)=f(1,2)+f(1,1)=0+1=1$
$f(5,2)=f(3,2)+f(3,1)=1+1=2$
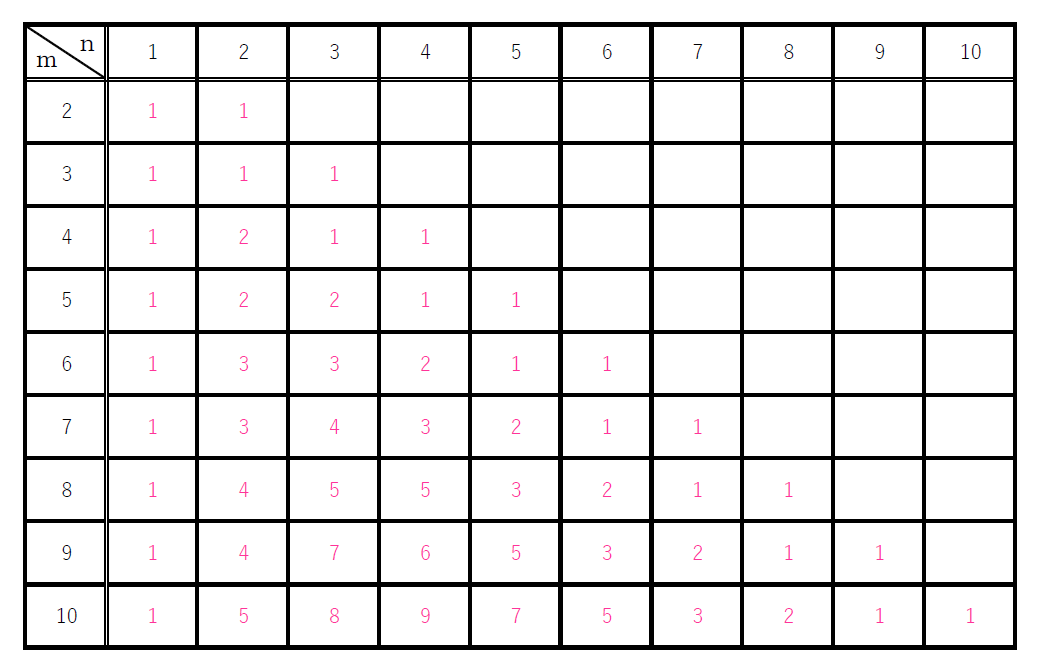
$次の表は、m=2~10,n=1~10までのf(m,n)の値をまとめたものです。$
$\hspace{4em}$
$この試行の全事象の総数は、ボールが入らない箱があってもよい場合の数であるが、初めから$
$ボールを箱の数だけ多くして、すべての箱に入れておく。$
$その後、元々のm個のボールをn個の箱に入れるが、このときは入らない箱があってもかまわない。$
$すると、m+n個のボールがn個の箱に少なくとも1個は入ることになるからその総数が全事象の$
$総数になり、 f(m+n,n) 通りである。$
$したがって、求める確率は$
$\hspace{2em} P(m,n)=\cfrac{f(m,n)}{f(m+n,n)}$
$ボールも箱も区別しないで、m個のボールをn個の箱に入れる(n組に分ける)とき、どのn個の箱にも少なくとも$
$1個のボールを入れる入れ方の確率は、どの入れ方も同様に確からしいとすると$
$\hspace{5em} P(m,n)=\cfrac{f(m,n)}{f(m+n,n)}$
$例えば例3では P(6,4)=\cfrac{f(6,4)}{f(10,4)}=\cfrac{2}{9} となり確かに一致する。$
$なお、m個のボールをn個の箱に入れる(n組に分ける)ことを(m_1,m_2,\cdots , m_n)と表したが$
$(1)\ すべての箱に少なくても1個のボールが入るような分け方は$
$\hspace{2em} 方程式 x_1+x_2+ \cdots +x_n=m における 1 \leqq x_1 \leqq x_2 \leqq \cdots \leqq x_n $
$\hspace{2em} を満たす整数解(x_1,x_2, \cdots ,x_n) を求めることに対応します。$
$(2)\ ボールが入らない箱があってもよいような分け方は$
$\hspace{2em} 方程式 x_1+x_2+ \cdots +x_n=m における 0 \leqq x_1 \leqq x_2 \leqq \cdots \leqq x_n $
$\hspace{2em} を満たす整数解(x_1,x_2, \cdots ,x_n) を求めることに対応しますので$
$\hspace{2em} x_1+1=y_1,\ x_2+1=y_2,\ \cdots ,\ x_n+1=y_n とおくと \hspace{2em} y_1 > 0,\ y_2 > 0,\ \cdots , y_n > 0 となり$
$\hspace{2em} (y_1-1)+(y_2-1)+ \cdots +(y_n-1)=m$
$\hspace{2em} よって$
$\hspace{2em} 方程式 y_1+y_2+ \cdots +y_n=m+n における \ 1 \leqq y_1 \leqq y_2 \leqq \cdots \leqq y_n$
$\hspace{2em} を満たす整数解(y_1,y_2, \cdots ,y_n) を求めることに対応します。$
ボールの分配 に戻る
メインメニュー に戻る