2.ボールは区別しないが、箱は区別する場合
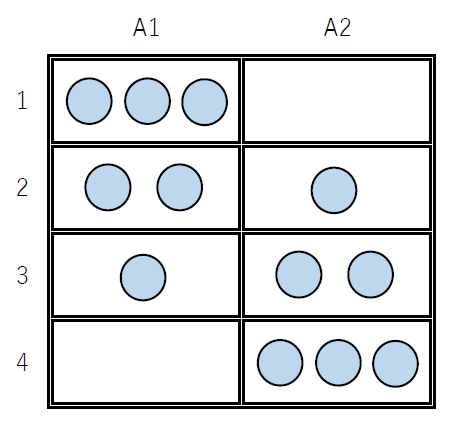
$全事象は、右図のとおりで4通りあるが、そのどれが起こる$
$ことも同様に確からしいとする。$
$どの箱にもボールが入っているのは右図の(2)(3)の場合で、$
$その確率は$
$\hspace{2em} P(3,2)=\cfrac{2}{4}=\cfrac{1}{2}$
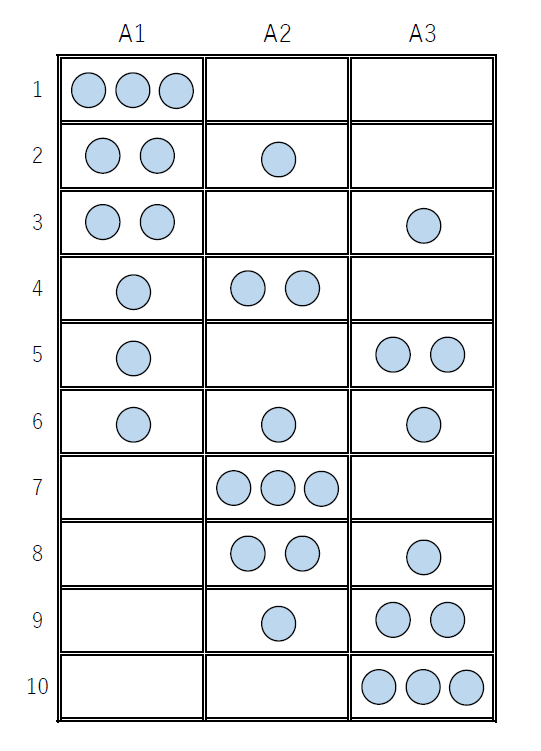
$例2 3個のボールを3つの箱A_1,A_2,A_3に入れる場合$
$全事象は、右図のとおり10通りあるが、そのどれが$
$起こることも同様に確からしいとする。$
$どの箱にもボールが入っているのは右図の(6)の場合$
$だけだから、その確率は$
$\hspace{2em} P(3,3)=\cfrac{1}{10}$
$なお、全事象は\{A_1,A_2,A_3\}から重複を許して3個とる$
$重複組合せとなる。$
$例えば、(3)は\{A_1,A_1,A_3\}ととった場合です。$
$したがって総数は$
$\hspace{2em} _3H_3=_5C_3=_5C_2=10$
$と求まります。$
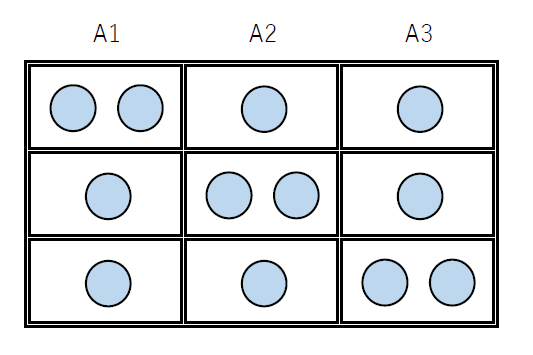
$例3 4個のボールを3つの箱A_1,A_2,A_3に入れる場合$
$全事象は、異なる3個 \{A_1,A_2,A_3 \} から重複を許し$
$て4個とる重複組合せである。したがって、総数は$
$\hspace{2em}_3H_4=_6C_4=_6C_2=\cfrac{6 \times 5}{2}=15$
$そのどれが起こることも同様に確からしいとする。$
$どの箱にもボールが入っているのは右図のとおり$
$3通りあるから、その確率は$
$\hspace{2em} P(4,3)=\cfrac{3}{15}=\cfrac{1}{5}$
$例4 m個のボールを3つの箱A_1,A_2,A_3に入れる場合(ただし m \geqq 3)$
$全事象は、異なる3個 \{A_1,A_2,A_3 \} から重複を許してm個とる重複組合せである。$
$したがって、その総数は$
$\hspace{2em} _3H_m=_{m+2}C_m=_{m+2}C_2=\cfrac{(m+2)(m+1)}{2}$
$そのどれが起こることも同様に確からしいとする。$
$どの箱にもボールが入っているようにするには$
$はじめに、1個ずつ3つの箱に入れると、少なくとも1個は入ったことになる。$
$次に、残り(m-3)個を3つの箱に入れればよい。$
$これは異なる3個から(m-3)個をとる重複組合せだから$
$\hspace{2em} _3H_{m-3}=_{m-1}C_{m-3}=_{m-1}C_2=\cfrac{(m-1)(m-2)}{2}$
$よって求める確率は$
$\hspace{2em} P(m,3)=\cfrac{_3H_{m-3}}{_3H_m}=\cfrac{(m-1)(m-2)}{(m+2)(m+1)}$
$例5 m個のボールをn個の箱に入れる場合(ただし m \geqq n)$
$ 全事象は、異なるn個から重複を許してm個とる重複組合せであるからその総数は$
$\hspace{2em} _nH_m=_{m+n-1}C_m=_{m+n-1}C_{n-1}\ \ 通り$
$で、そのどれが起こることも同様に確からしいとする。$
$どの箱にもボールが入っているようにするには$
$はじめに、1個ずつn個の箱に入れると、少なくとも1個は入ったことになる。$
$次に、残り(m-n)個をn個の箱に入れればよい。$
$これは異なるn個から(m-n)個をとる重複組合せだから$
$\hspace{2em} _nH_{m-n}=_{m-1}C_{m-n}=_{m-1}C_{n-1}$
$よって求める確率は$
$\hspace{2em} P(m,n)=\cfrac{_nH_{m-n}}{_nH_m}=\cfrac{_{m-1}C_{n-1}}{_{m+n-1}C_{n-1}}$
$\qquad m個のボールをn個の箱に入れるとき、どの箱にも少なくとも1個のボールが入る確率は$
$\hspace{4em} P(m,n)=\cfrac{_nH_{m-n}}{_nH_m}=\cfrac{_{m-1}C_{n-1}}{_{m+n-1}C_{n-1}} \qquad ただし m \geqq n $
ボールの分配 に戻る
メインメニュー に戻る