MY MATH NOTE

　
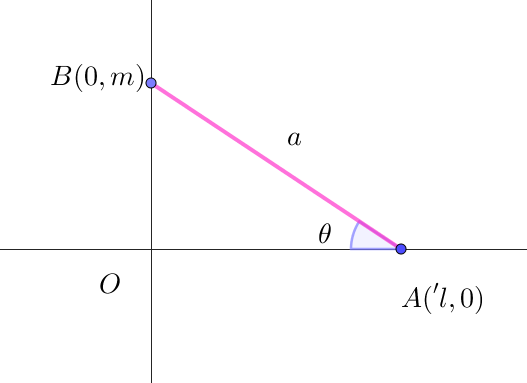
$長さ \ a\ の線分 \ AB\ の端点 \ A\ が \ x\ 軸上にあり、端点 \ B\ が \ y\ 軸上にあるとする。$
$このとき点 \ A,\ B\ が動いてできる$包絡線$を求めてみましょう。$

$A(l,\ 0),\ \ B(0,\ m)とすると \quad 直線 \ AB\ の方程式は \quad \cfrac{x}{l}+\cfrac{y}{m}=1$

$第 \ 1\ 象限では、\angle OAB=\theta \ \ (0 \leqq \theta \leqq \cfrac{\pi}{2}) \quad とおくと \quad l=a\cos \theta,\quad m=a\sin \theta \quad だから$

$ \quad \cfrac{x}{a\cos \theta }+\cfrac{y}{a\sin \theta }=1$

　
$\quad x\sin \theta + y\cos \theta =a\sin \theta \cos \theta \hspace{8em}(1)$

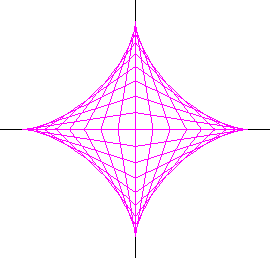
$右図は、\theta をパラメータとしてこの直線をかいたグラフです。$

$線分ABが第2～第4象限にあるときは対称性で求められます。$


$(1)を\theta で偏微分して$

$\qquad x\cos \theta - y\sin \theta =a\cos ^2 \theta - a\sin ^2 \theta \hspace{5em}(2)$

$(1) \times \sin \theta + (2) \times \cos \theta \ \ より$
$\qquad x\sin ^2 \theta +x\cos ^2 \theta =a\cos ^3 \theta$
$\qquad \therefore x=a\cos ^3 \theta$

$(1)に代入して$
$\qquad a\cos ^3 \theta sin \theta + y\cos \theta =a\sin \theta \cos \theta $
\begin{eqnarray*} \qquad y &=&a \sin \theta - a\cos ^2 \theta \sin \theta \\ \\ &=&a \sin \theta (1- \cos ^2 \theta ) \\ \\ &=&a \sin ^3 \theta \\ \end{eqnarray*}

　
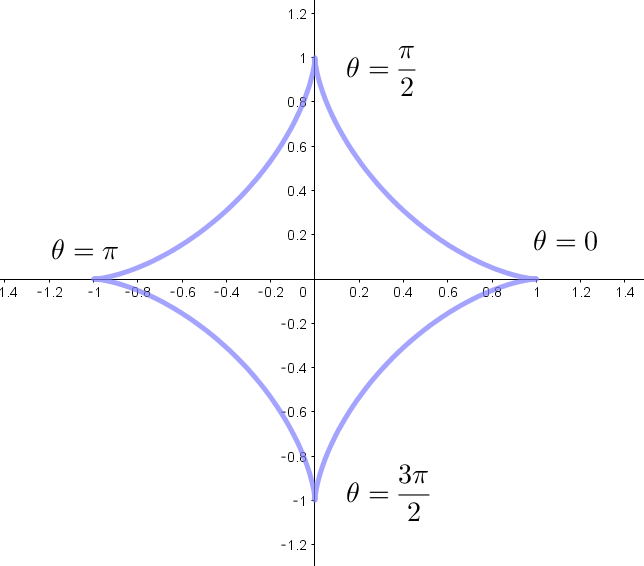
$包絡線 \quad x=a\cos ^3 \theta,\quad y=a \sin ^3 \theta \quad をアステロイドといいます。$

$右図は \ a=1 \ の場合のアステロイドのグラフです。$

$また、\theta \ \ を消去して$

$x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}\cos ^2 \theta +a^{\frac{2}{3}}\sin ^2 \theta =a^{\frac{2}{3}}$

$\therefore \ \ x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}$

$これは、アステロイドの \ xy\ 表示です。$

ページの先頭へ↑