包絡線
1 直線群が通る(通らない)領域
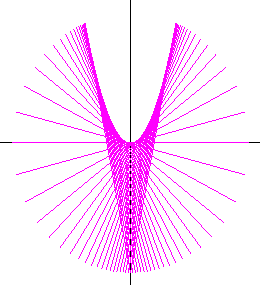
$例1$
$直線 y=\cfrac{1}{2}tx-t^2\ \ でtの値を変化させたとき、グラフが$
$通る領域は右図のとおりで、その境界は簡単に求まります。$
$\qquad 2t^2-xt+2y=0 \ \ で\ tは実数だから$
$\qquad D=x^2-16y \geqq 0$
$したがって$
$\qquad y \leqq \cfrac{1}{16}x^2$
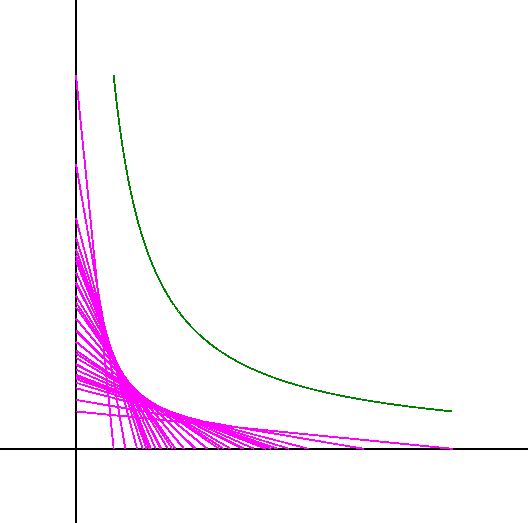
$例2$
$双曲線 y=\cfrac{1}{x}\ \ 上の任意の点A(t,\cfrac{1}{t})に対し、$
$\qquad P(t,0),\ \ Q(0,\cfrac{1}{t})\ \ とする。$
$tの値を変化させたとき、直線PQが通る領域は右図の通りで、やはり$
$双曲線になりそうですが、次のように求まります。$
$直線PQの方程式は$
$\qquad \cfrac{x}{t}+ty=1 \ \ より$
$\qquad t^2y-t+x=0 \ \ でtは実数だから$
$\qquad D=1-4xy \geqq 0$
$したがって$
$\qquad y \leqq \cfrac{1}{4x}$
2 包絡線
$例1の \ \ y =\cfrac{1}{16}x^2,\ \ 例2の \ \ y = \cfrac{1}{4x} \ のように直線群が決して通らない領域の境界を「包絡線」といいます。$
$この直線群と包絡線にはある性質があります。$
$例1については$
$\quad 直線 \ \ y=\cfrac{1}{2}tx-t^2 \ と包絡線 \ \ y =\cfrac{1}{16}x^2 \ の交点は$
$\qquad \cfrac{1}{2}tx-t^2 =\cfrac{1}{16}x^2 \ \ より$
$\qquad x^2-8tx+16t^2=0$
$\qquad (x-4t)^2=0$
$\qquad \therefore x=4t \ \ (重解)$
$\quad よって、直線は包絡線の接線です。$
$例2については$
$\quad 直線 \ \ t^2y-t+x=0 \ と包絡線 \ \ y = \cfrac{1}{4x} \ の交点は$
$\qquad t^2 \times \cfrac{1}{4x} -t+x=0 \ \ より$
$\qquad x^2-tx+\cfrac{t^2}{4}=0$
$\qquad (x-\cfrac{t}{2})^2=0$
$\qquad \therefore x=\cfrac{t}{2}\ \ (重解)$
$\quad やはり、直線は包絡線の接線です。$

$そこで、包絡線は次のように定義されています。$
$曲線Lが、曲線群C:f(x,y,t)=0 \ \ (tはパラメータ)と、ある点で$
$接するとき、$ LをCの包絡線 $といいます。$
$それでは、曲線群C:f(x,y,t)=0 \ \ が与えられたとき、包絡線Lの$
$求め方について考えましょう。$
$L上の任意の接点をP(x,y)とすると、点PはC上の点でもあるから$
$\qquad f(x,y,t)=0 \hspace{25em}(1)$
$これをxで微分して$
$\qquad \cfrac{\partial f}{\partial x }+ \cfrac{\partial f}{\partial y}\cfrac{dy}{dx} =0 \hspace{23em}(2)$
$接点P(x,y)はパラメータtごとに異なるからtの関数です。$
$よって、\cfrac{dy}{dx}=\cfrac{\cfrac{dy}{dt}}{\cfrac{dx}{dt}}$
$(2)に代入して$
$\qquad \cfrac{\partial f}{\partial x }\cfrac{dx}{dt}+ \cfrac{\partial f}{\partial y}\cfrac{dy}{dt} =0 \hspace{21em}(3)$
$また、(1)をtで微分すると$
$\qquad \cfrac{\partial f}{\partial x }\cfrac{dx}{dt}+ \cfrac{\partial f}{\partial y}\cfrac{dy}{dt} +\cfrac{\partial f}{\partial t }=0 $
$(3)を代入すると$
$\qquad \cfrac{\partial f}{\partial t }=0 $
$曲線群C:f(x,y,t)=0 \ \ の包絡線Lは$
\[
\left\{ \begin{array}{l}
f(x,y,t)=0\\
\cfrac{\partial f}{\partial t }=0 \\
\end{array} \right.
\]
$例1で確認しましょう。$
$\quad y=\cfrac{1}{2}tx-t^2 \ \ より f(x,y,t)=\cfrac{1}{2}tx-y-t^2\ \ とおくと$
$\qquad f(x,y,t)=0 \ \ より \cfrac{1}{2}tx-y-t^2 =0 \hspace{10em}(1)$
$\qquad \cfrac{\partial f}{\partial t }=\cfrac{1}{2}x-2t=0 \ \ より\ \ t=\cfrac{1}{4}x$
$(1)に代入して$
$\qquad \cfrac{1}{2} \times \cfrac{1}{4}x^2-y-\big(\cfrac{1}{4}x\big)^2=0$
$\qquad \therefore y=\cfrac{1}{16}x^2$
$となって、確かに一致します。$
$例2はどうでしょうか。$
$\quad f(x,y,t)=x+t^2y-t\ \ とおくと$
$\qquad f(x,y,t)=0 \ \ より x+t^2y-t =0 \hspace{10em}(2)$
$\qquad \cfrac{\partial f}{\partial t }=2ty-1=0 \ \ より \ \ t=\cfrac{1}{2y}$
$(2)に代入して$
$\qquad x+\cfrac{1}{4y} -\cfrac{1}{2y}=0$
$\qquad \therefore y=\cfrac{1}{4x}$
$となって、一致します。$
3 中心角が一定な直線がえがく包絡線
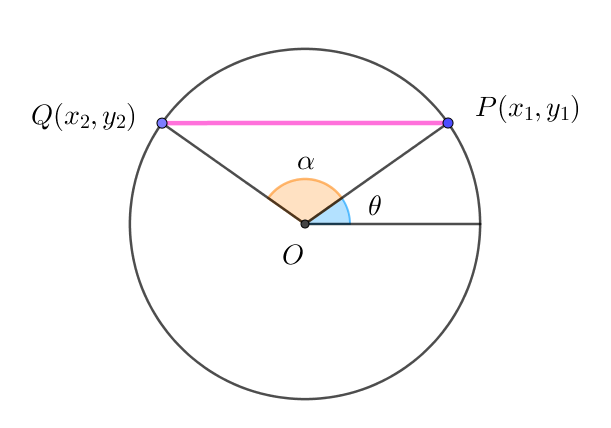
$単位円周上の2点P,Qの中心角を\alpha (一定)とし、点Pがx軸の$
$正方向となす角を\theta とする。$
$\theta が変化するとき、直線PQの包絡線を求めてみましょう。$
$x_1=\cos \theta,\ \ y_1=\sin \theta,\ \ x_2=\cos (\theta +\alpha ),\ \ y_2=\sin (\theta +\alpha )$
$ とおくと、直線PQの方程式は$
$\quad y-\sin \theta =\cfrac{\sin (\theta + \alpha )-\sin \theta }{\cos (\theta +\alpha )-\cos \theta }(x-\cos \theta )$
$\quad (y-\sin \theta)\{\cos (\theta +\alpha )-\cos \theta \}=(x-\cos \theta )\{\sin (\theta + \alpha )-\sin \theta \} \hspace{10em}(1)$
$両辺を\theta で微分して$
$-\cos \theta \{\cos (\theta +\alpha )-\cos \theta \}+(y-\sin \theta)\{-\sin (\theta +\alpha )+\sin \theta \} =\sin \theta \{\sin (\theta + \alpha )-\sin \theta \} +(x-\cos \theta )\{\cos (\theta + \alpha )-\cos \theta \} $
$-\cos \theta \cos (\theta +\alpha )+\cos ^2 \theta +(y-\sin \theta)\{-\sin (\theta +\alpha )+\sin \theta \}=\sin \theta \sin (\theta + \alpha )-\sin ^2 \theta +(x-\cos \theta )\{\cos (\theta + \alpha )-\cos \theta \} $
$\qquad (y-\sin \theta)\{\sin (\theta +\alpha )-\sin \theta \}+(x-\cos \theta )\{\cos (\theta + \alpha )-\cos \theta \} $
$\qquad =-\{\cos (\theta +\alpha )\cos \theta +\sin (\theta +\alpha ) \sin \theta \}+\cos ^2 \theta +\sin ^2 \theta $
$\qquad =-\cos (\theta +\alpha - \theta) +1$
$\qquad =1-\cos \alpha \hspace{32em}(2)$
$ここで、p=\cos (\theta + \alpha )-\cos \theta ,\ \ q=\sin (\theta +\alpha )-\sin \theta \ \ とおくと$
$(1)は p(y-\sin \theta )=q(x- \cos \theta )$
$\qquad py-qx=p\sin \theta -q\cos \theta \hspace{26em}(3)$
$(2)は q(y-\sin \theta )+p(x- \cos \theta )=1-\cos \alpha $
$\qquad qy+px=q\sin \theta +p\cos \theta +1-\cos \alpha \hspace{21em}(4)$
$(3)^2+(4)^2$
$\hspace{3em} (py-qx)^2+(qy+px)^2=(p\sin \theta -q\cos \theta)^2+(q\sin \theta +p\cos \theta +1-\cos \alpha)^2$
\begin{eqnarray*}
(p^2+q^2)(x^2+y^2)
&=&(p^2+q^2)\sin ^2 \theta +(p^2+q^2)\cos ^2\theta +(1-\cos \alpha )^2+2p(1-\cos \alpha )\cos \theta +2q(1-\cos \alpha )\sin \theta \\
\\
&=&(p^2+q^2) +(1-\cos \alpha )^2+2p(1-\cos \alpha )\cos \theta +2q(1-\cos \alpha )\sin \theta \hspace{8em}(5)\\
\end{eqnarray*}
$ここで、$
\begin{eqnarray*}
p^2+q^2
&=&\{\cos (\theta +\alpha )-\cos \theta \}^2+\{\sin (\theta +\alpha )-\sin \theta \}^2\\
&=&2-2\{\cos (\theta +\alpha )\cos \theta +\sin (\theta +\alpha )\sin \theta \}\\
&=&2-2\cos ((\theta +\alpha -\theta )\\
&=&2-2\cos \alpha\\
\end{eqnarray*}
$よって(5)は$
$\qquad 2(1-\cos \alpha)(x^2+y^2)=2(1-\cos \alpha)+(1-\cos \alpha )^2+2(1-\cos \alpha )(p\cos \theta +q\sin \theta) \hspace{10em}(6)$
$ここで、$
\begin{eqnarray*}
p\cos \theta +q\sin \theta
&=&\cos \theta \{\cos (\theta +\alpha )-\cos \theta \}+\sin \theta \{\sin (\theta +\alpha )-\sin \theta \}\\
&=&\cos (\theta +\alpha )\cos \theta +\sin (\theta +\alpha )\sin \theta -1\\
&=&\cos (\theta +\alpha -\theta ) -1\\
&=&-(1-\cos \alpha ) \\
\end{eqnarray*}
$よって(6)は$
\begin{eqnarray*}
2(1-\cos \alpha)(x^2+y^2)
&=&2(1-\cos \alpha)+(1-\cos \alpha )^2-2(1-\cos \alpha )^2\\
&=&2(1-\cos \alpha)-(1-\cos \alpha )^2\\
\end{eqnarray*}
$\qquad \therefore 2(x^2+y^2)=2-(1-\cos \alpha)=1+\cos \alpha $
$\qquad (x^2+y^2)=\cfrac{1}{2}(1+\cos \alpha)=\cos ^2 \cfrac{\alpha}{2}$
$これで、包絡線は、原点中心、半径 \ |\cos \cfrac{\alpha}{2}| \ の円であることがわかりました。$
4 クレロー(仏 1713-1765)の微分方程式
$p=\cfrac{dy}{dx} \ \ として、y=xp+f(p) \hspace{15em}(1)$
$の形の微分方程式をクレローの微分方程式といいます。$
$(1)をxで微分すると$
$\qquad y'=(p+xp')+\cfrac{df(p)}{dp}\cfrac{dp}{dx}$
$\qquad p=(p+xp')+\cfrac{df(p)}{dp}p'$
$\qquad p'(\cfrac{df(p)}{dp}+x)=0$
$\qquad p'=0,\quad \cfrac{df(p)}{dp}+x=0$
(i)$\ \ p'=0 \ \ のとき$
$\qquad p=C\ (定数)だから(1)に代入して$
$\qquad y=Cx+f(C) \qquad これは一般解となります。$
(ii)$\ \ \cfrac{df(p)}{dp}+x=0 \ \ のとき$
$これは$(i)$の \ y=Cx+f(C) をCで偏微分した x+\cfrac{df(C)}{dC}=0\ \ でCをpで置き換えたものになっています。$
$したがって、このクレローの微分方程式の一般解 \ \ y=Cx+f(C) \ \ の表す直線群の包絡線が$
$この$(ii)$の解の曲線である。このような解を「特異解」といいます。$
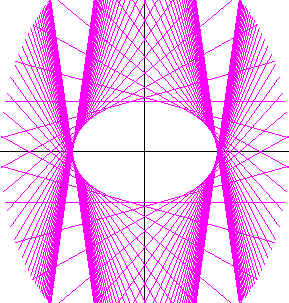
$例 \quad y=xp+\sqrt{b^2+a^2p^2} \ \ (a > 0,b > 0)$
$一般解は、p \rightarrow C \ \ とおいて$
$\qquad y=Cx+\sqrt{b^2+a^2C^2} \hspace{17em}(2)$
$特異解は、これをCで偏微分して$
$\qquad 0=x+\cfrac{a^2C}{\sqrt{b^2+a^2C^2}}$
$\qquad x=-\cfrac{a^2C}{\sqrt{b^2+a^2C^2}}$
$\qquad \therefore x^2=\cfrac{a^4C^2}{b^2+a^2C^2}$
$xを(2)に代入して$
 \begin{eqnarray*}
y
&=&-\cfrac{a^2C^2}{\sqrt{b^2+a^2C^2}}+\sqrt{b^2+a^2C^2}\\
\\
&=&-\cfrac{-a^2C^2+(b^2+a^2C^2)}{\sqrt{b^2+a^2C^2}}\\
\\
&=&\cfrac{b^2}{\sqrt{b^2+a^2C^2}}\\
\\
\end{eqnarray*}
$\qquad \therefore y^2=\cfrac{b^4}{b^2+a^2C^2}$
\begin{eqnarray*}
y
&=&-\cfrac{a^2C^2}{\sqrt{b^2+a^2C^2}}+\sqrt{b^2+a^2C^2}\\
\\
&=&-\cfrac{-a^2C^2+(b^2+a^2C^2)}{\sqrt{b^2+a^2C^2}}\\
\\
&=&\cfrac{b^2}{\sqrt{b^2+a^2C^2}}\\
\\
\end{eqnarray*}
$\qquad \therefore y^2=\cfrac{b^4}{b^2+a^2C^2}$
$したがって$
$\qquad \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=\cfrac{a^2C^2}{b^2+a^2C^2}+\cfrac{b^2}{b^2+a^2C^2}=1$
$これで、特異解は楕円であることがわかりました。$
メインメニュー に戻る