リーマン・ルベーグの定理
$この定理は、狭義のフーリェ級数の収束性の根拠となるものですので、前もって$狭義のフーリェ級数$をご覧ください。$
$簡単に復習します。$
$\quad f(x)\ は \ 2\pi\ を周期とする、区分的になめらかな周期関数とします。$
$\quad 区間 \ [-\pi,\ \pi]\ において \ \ \{1,\ \cos nx,\ \sin nx\}\ \ (n=1,\ 2,\ \cdots )\ \ は直交系をなし、\{\cfrac{1}{\sqrt{2\pi}},\cfrac{1}{\sqrt{\pi}}\cos nx,\cfrac{1}{\sqrt{\pi}}\sin nx\}\ \ は$
$\quad 正規直交系となります。$
\[関数 \ f(x)\ が、区間 \ [-\pi,\ \pi]\ 上の正規直交系 \ \ \{\varphi_n(x)\}\ \ によって、f=\sum_{i=0}^{\infty} c_i\varphi_i \ \ とあらわされるとき\] \[\quad c_n=(\varphi_n,f)=\int _a^b f(x)\varphi_n(x)dx \quad より\] \[\qquad c_0=(\varphi_0,f)=\cfrac{1}{\sqrt{2\pi}}\int _{-\pi}^{\pi}f(x)dx \] \[\qquad c_{2n-1}=(\varphi_{2n-1},f)=\cfrac{1}{\sqrt{\pi}}\int _{-\pi}^{\pi} f(x)\cos nx dx \] \[\qquad c_{2n}=(\varphi_{2n},f)=\cfrac{1}{\sqrt{\pi}}\int _{-\pi}^{\pi} f(x)\sin nx dx \] $したがって$
\begin{eqnarray*} f(x) &=&\sum_{n=0}^{\infty} c_n\varphi_n \\ &=&c_0\varphi_0 + \sum_{n=1}^{\infty} (c_{2n-1}\varphi_{2n-1}+c_{2n}\varphi_{2n}) \\ &=&\cfrac{1}{2\pi}\int _{-\pi}^{\pi}f(x)dx + \sum_{n=1}^{\infty} \Big\{\big (\cfrac{1}{\pi}\int _{-\pi}^{\pi} f(x)\cos nx dx\big)\cos nx + \big(\cfrac{1}{\pi}\int _{-\pi}^{\pi} f(x)\sin nx dx \big)\sin nx \Big\}\\ \end{eqnarray*}
$ここで$
\[a_0=\cfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx ,\qquad a_n=\cfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx , \qquad b_n=\cfrac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx を(狭義の)フーリェ係数といい、\] \[f(x)=\cfrac{a_0}{2}+\sum_{n=1}^\infty (a_n\cos nx+b_n\sin nx) \ \ を \ f(x)\ の(狭義の)フーリェ級数展開といいます。\]
$リーマン・ルベーグの定理$
$\quad f(x) \ は \ [-\pi,\ \pi]\ で積分可能な関数であるとき$
\[\quad \lim_{n \rightarrow \infty} \int _{-\pi}^{\pi} f(x)\cos nx dx=0,\qquad \lim_{n \rightarrow \infty} \int _{-\pi}^{\pi} f(x)\sin nx dx=0\]
$(証明)$
\[ベッセルの不等式 \quad \sum_{i=1}^\infty c_i^2 \leqq ||f||^2 \quad より\] \[||f|\ が有限ならば、左辺は正項級数だから\quad \sum_{i=1}^\infty c_i^2 \ \ は上に有界な単調増加となり収束する。\] $すなわち \quad n \longrightarrow \infty \quad のとき \quad c_n \longrightarrow 0 \quad となるから \quad a_n \longrightarrow 0,\quad b_n \longrightarrow 0 \quad となります。$
$他に階段関数をつかう証明法もありますが、参考書をあたってください。$
$わかったようでわからないこの定理の意味するところを考えてみましょう。$
$n\ を大きくすると \ \ \cos nx,\ \ \sin nx \ \ の周期が小さくなり、逆に振動数が増えます。$
$下図は、y=x\cos 10x \ \ と \ \ y=\sqrt{x}\cos 10x \ \ のグラフです。$
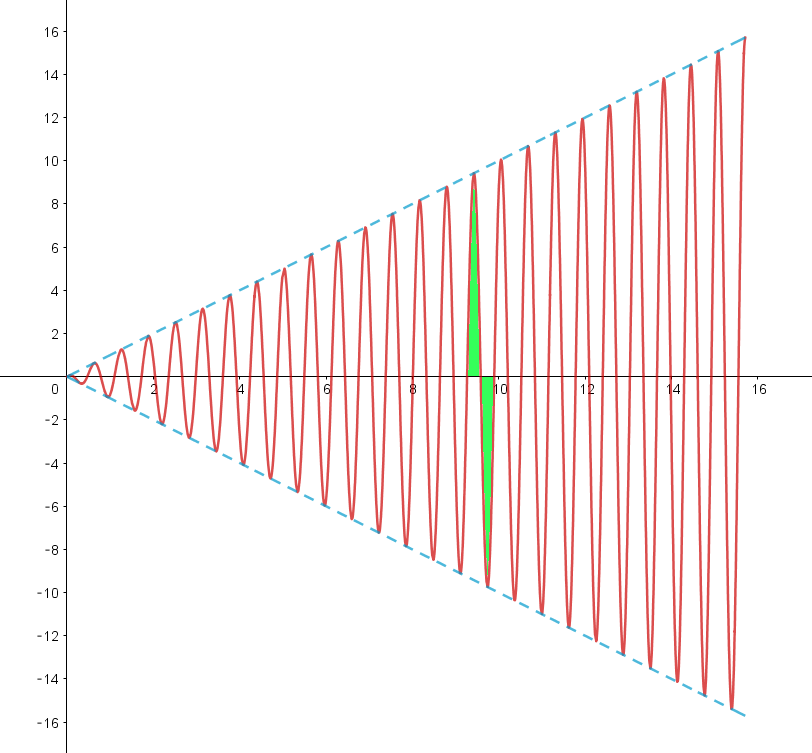
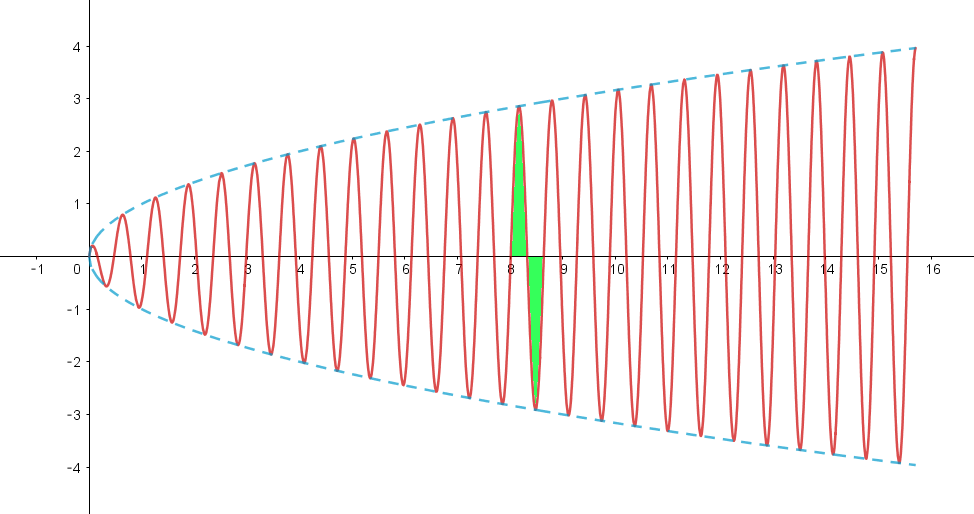
$余弦関数なので、正の部分と負の部分が交互にあらわれ、n=10\ \ ですが、激しく振動していることがわかります。$
$1\ 周期分の区間が小さいので、ある正の部分の面積とその次の負の部分の面積はほとんど等しくなります。$
$すなわち、この1\ 周期分の定積分の値はほとんど \ 0\ ということです。$
$具体的に、y=x\cos nx \ \ について計算します。$
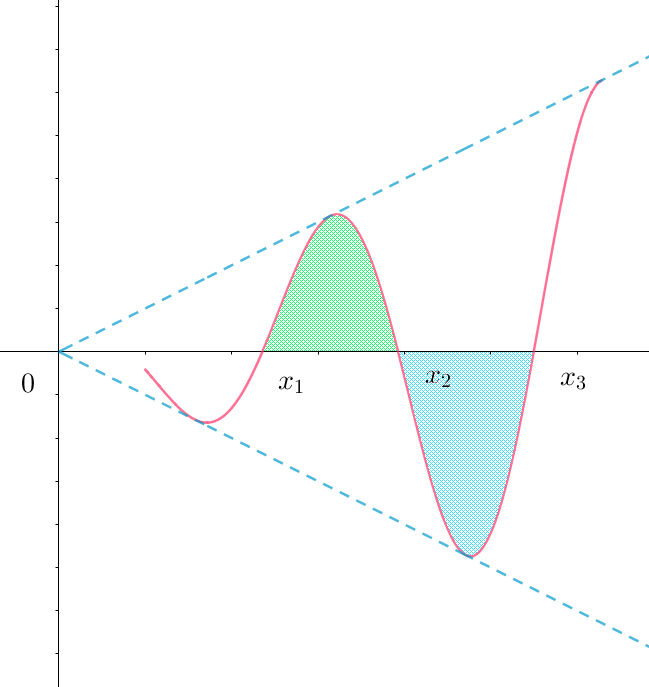
$\quad \cos nx \ \ が \ x\ 軸と交わる連続する \ 3\ 点を \ \ x_1,\ x_2,\ x_3 \ \ とすると$
$\quad \cos nx=0 \quad より \quad nx=m\pi +\cfrac{\pi}{2}\ \ (m\ は整数) \quad \therefore \ \ x=(\cfrac{m}{n}+\cfrac{1}{2n})\pi$
$したがって$
$\quad x_1=(\cfrac{m}{n}+\cfrac{1}{2n})\pi,\quad x_2=(\cfrac{m+1}{n}+\cfrac{1}{2n})\pi,\quad x_3=(\cfrac{m+2}{n}+\cfrac{1}{2n})\pi$
$よって$
$\quad \sin nx_1=\sin \big(m+\cfrac{1}{2}\big)\pi=(-1)^m,\qquad \cos nx_1=\cos \big(m+\cfrac{1}{2}\big)\pi=0$
$\quad \sin nx_3=\sin \big(m+2+\cfrac{1}{2}\big)\pi=(-1)^m ,\qquad \cos nx_3=\cos \big(m+2+\cfrac{1}{2}\big)\pi=0$
\begin{eqnarray*}
I_1+I_2
&=&\int _{x_1}^{x_3}x\cos nxdx\\
&=&\big[\cfrac{1}{n}x\sin nx\big] _{x_1}^{x_3}-\int _{x_1}^{x_3}\cfrac{1}{n}\sin nxdx\\
&=&\cfrac{1}{n}(x_3\sin nx_3 -x_1\sin nx_1)+ \cfrac{1}{n^2}\big[\cos nx\big]_{x_1}^{x_3}\\
&=&\cfrac{1}{n}(x_3\sin nx_3 -x_1\sin nx_1)+ \cfrac{1}{n^2}(\cos nx_3- \cos nx_1)\\
&=&\cfrac{\pi}{n}\big\{(\cfrac{m+2}{n}+\cfrac{1}{2n})(-1)^m -(\cfrac{m}{n}+\cfrac{1}{2n})(-1)^m \big\}\\
&=&\cfrac{2\pi}{n^2}(-1)^m \\
\end{eqnarray*}
$したがって \quad n \longrightarrow \infty \quad とすると \quad I_1+I_2 \longrightarrow 0$
$なお、この定理は、一般に区間 \ [a,\ b]\ で成りたちます。$
\[\lim_{n \rightarrow \infty} \int _a^b f(x)\cos nx dx=0,\qquad \lim_{n \rightarrow \infty} \int _a^b f(x)\sin nx dx=0\]
メインメニュー に戻る