フーリェ変換の複素数表示
$\qquad $フーリェ積分定理$より$
\[f(x) \ が区分的になめらかで \ \ \int_{-\infty}^{\infty}|f(x)|dx < \infty \quad (絶対積分可能)ならば\] \[\quad \cfrac{1}{2}\big\{f(x+0)+f(x-0)\big\}=\cfrac{1}{\pi}\int _0^{\infty}\int _{-\infty}^{\infty}f(t)\cos \omega(x-t)dtd\omega\] $f(x)\ が連続な点では \quad \cfrac{1}{2}\big\{f(x+0)+f(x-0)\big\}=f(x)$
$\cos \omega(x-t)= \cfrac{1}{2}(e^{i\omega(x-t)}+e^{-i\omega(x-t)}) \quad であることをつかって$
$(1)\ \ フーリェ変換の複素数表示$
\begin{eqnarray*} f(x) &=&\cfrac{1}{\pi}\int _0^{\infty}\int _{-\infty}^{\infty}f(t)\cos \omega(x-t)dtd\omega\\ \\ &=&\cfrac{1}{2\pi}\int _0^{\infty}\int _{-\infty}^{\infty}f(t)\big(e^{i\omega(x-t)} + e^{-i\omega(x-t)}\big)dtd\omega\\ \\ & & \qquad 被積分関数は積分域で連続だから積分の順序を交換して\\ \\ &=&\cfrac{1}{2\pi}\int _{-\infty}^{\infty} f(t) \Big\{\int _0^{\infty}e^{i\omega(x-t)} d\omega + \int _0^{\infty}e^{-i\omega(x-t)} d\omega \Big\} dt\\ \\ & & \qquad 積分の第 \ 2\ 項で、\omega \longrightarrow -\omega \quad とおくと\\ \\ &=&\cfrac{1}{2\pi}\int _{-\infty}^{\infty} f(t) \Big\{\int _0^{\infty}e^{i\omega(x-t)} d\omega + \int _0^{-\infty}e^{i\omega(x-t)} (-d\omega) \Big\} dt\\ \\ &=&\cfrac{1}{2\pi}\int _{-\infty}^{\infty} f(t) \Big\{\int _0^{\infty}e^{i\omega(x-t)} d\omega + \int _{-\infty}^0 e^{i\omega(x-t)} d\omega \Big\} dt\\ \\ &=&\cfrac{1}{2\pi}\int _{-\infty}^{\infty} \int _{-\infty}^{\infty} f(t)e^{i\omega(x-t)} d\omega dt\\ \\ &=&\int _{-\infty}^{\infty}\Big\{ \cfrac{1}{2\pi}\int _{-\infty}^{\infty} f(t)e^{-i\omega t} dt \Big\} e^{i\omega x} d\omega \\ \end{eqnarray*}
\[\quad F(\omega)= \cfrac{1}{2\pi}\int _{-\infty}^{\infty} f(t)e^{-i\omega t} dt \quad とおくと\]
\[\quad f(x)=\int _{-\infty}^{\infty}F(\omega) e^{i\omega x} d\omega \]
$これが複素数表示のフーリェ変換とその逆変換の式です。$
$(2)\ \ コサイン変換、サイン変換$
\begin{eqnarray*} f(x) &=&\cfrac{1}{\pi}\int _0^{\infty}\int _{-\infty}^{\infty}f(t)\cos \omega(x-t)dtd\omega\\ \\ &=&\cfrac{1}{\pi}\int _0^{\infty}\int _{-\infty}^{\infty}(f(t)\cos \omega x \cos \omega t + f(t)\sin \omega x \sin \omega t)dtd\omega\\ \\ &=&\int _0^{\infty}\Big\{\Big(\cfrac{1}{\pi}\int _{-\infty}^{\infty}(f(t)\cos \omega tdt\Big) \cos \omega x + \Big(\cfrac{1}{\pi}\int _{-\infty}^{\infty}(f(t)\sin \omega tdt\Big) \sin \omega x\Big\}d\omega\\ \end{eqnarray*} \[\quad c(\omega)=\cfrac{1}{\pi}\int _{-\infty}^{\infty}f(t) \cos \omega tdt ,\qquad s(\omega)=\cfrac{1}{\pi}\int _{-\infty}^{\infty}f(t) \sin \omega tdt \quad とおくと\] \[f(x)=\int _0^{\infty} \big(c(\omega)\cos \omega x + s(\omega)\sin \omega x \big) d\omega \] $が得られます。とくに$
(i)$\ \ f(x)\ が偶関数のとき$
$\qquad f(t)\sin \omega t \quad は奇関数となるから \quad s(w)=0$
\[ c(\omega)=\cfrac{1}{\pi}\int _{-\infty}^{\infty}f(t) \cos \omega tdt =\cfrac{2}{\pi}\int _0^{\infty}f(t) \cos \omega tdt\] \[f(x)=\int _0^{\infty} c(\omega)\cos \omega xd\omega \]
$\quad となり、これらをそれぞれ、余弦変換(コサイン変換)、逆余弦変換(コサイン逆変換)\quad といいます。$
(ii)$\ \ f(x)\ が奇関数のとき$
$\qquad f(t)\cos \omega t \quad は奇関数となるから \quad c(w)=0$
\[ s(\omega)=\cfrac{1}{\pi}\int _{-\infty}^{\infty}f(t) \sin \omega tdt =\cfrac{2}{\pi}\int _0^{\infty}f(t) \sin \omega tdt\] \[f(x)=\int _0^{\infty} s(\omega)\sin \omega xd\omega \]
$\quad となり、これらをそれぞれ、正弦変換(サイン変換)、逆正弦変換(サイン逆変換)\quad といいます。$
$なお、F(\omega) の複素数表示でc(\omega)とs(\omega)を用いると$
\[F(\omega)= \cfrac{1}{2\pi}\int _{-\infty}^{\infty} f(t)e^{-i\omega t} dt=\cfrac{1}{2\pi}\int _{-\infty}^{\infty}(f(t)\cos \omega t -if(t)\sin \omega t)dt=\cfrac{1}{2}\{c(\omega)-is(\omega)\} \] $と表すことができます。$
$例1 \quad 右図のグラフのような指数関数(a > 0)の$
$\quad フーリェ変換を求めてみましょう。$
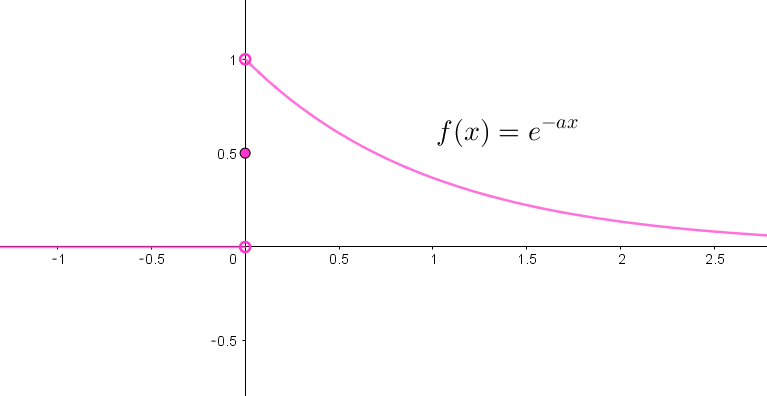
\[
f(x)=
\hspace{1em}
\left\{ \begin{array}{l}
0 \quad ( x < 0)\\
\cfrac{1}{2} \quad (x=0)\\
e^{-ax} \quad (x > 0 )\\
\end{array} \right.
\]
\begin{eqnarray*}
F(\omega)
&=&\cfrac{1}{2\pi}\int_{-\infty}^{\infty} f(t)e^{-i\omega t}dt\\
&=&\cfrac{1}{2\pi}\int_0^{\infty} e^{-at}e^{-i\omega t}dt\\
&=&\cfrac{1}{2\pi}\int_0^{\infty} e^{-(a+i\omega)t}dt\\
&=&-\cfrac{1}{2\pi(a+i\omega)}\big[e^{-(a+i\omega)t}\big]_0^{\infty} \hspace{3em} (*)\\
&=&\cfrac{1}{2\pi(a+i\omega)}\\
&=&\cfrac{a-i\omega}{2\pi(a^2+\omega ^2)}\\
\end{eqnarray*}
$(*)について$
$\qquad |e^{i\omega t}|=|\cos \omega t +i\sin \omega t|=1 \quad より \quad |e^{-(a+i\omega t)}=|e^{-at}||e^{i\omega t}|=|e^{-at}|$
$\qquad a > 0 \quad だから \quad t \longrightarrow \infty \quad のとき \quad e^{-at} \longrightarrow 0 \quad したがって \quad e^{-(a+i\omega)t} \longrightarrow 0$
$\quad F(\omega)=\cfrac{1}{2}\{c(\omega)-is(\omega)\} \quad より \quad c(\omega)=\cfrac{a}{\pi(a^2+\omega ^2)},\qquad s(\omega)=\cfrac{\omega}{\pi(a^2+\omega ^2)}$
(i)$\ \ x > 0\ のグラフを \ y\ 軸に関して対称にしたものを付加して偶関数に直すと$
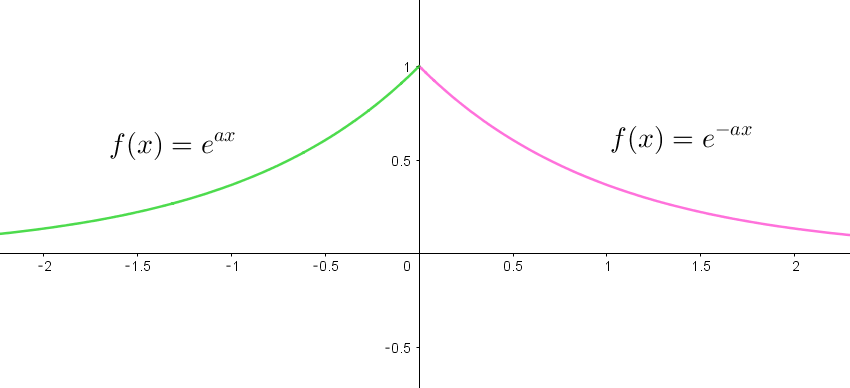
\[
f(x)=
\hspace{1em}
\left\{ \begin{array}{l}
e^{ax} \quad ( x < 0)\\
1 \quad (x=0)\\
e^{-ax} \quad (x > 0 )\\
\end{array} \right.
\]
$逆変換は$
\[f(x)=\int _{-\infty}^{\infty} c(\omega)\cos \omega xd\omega = \int _0^{\infty} \cfrac{2a}{\pi(a^2+\omega ^2)}\cos \omega xd\omega\]
$これが \quad f(x)=e^{-ax} \quad に一致するから$
\[\int _0^{\infty} \cfrac{2a}{\pi(a^2+\omega ^2)}\cos \omega xd\omega=e^{-ax} \qquad \therefore \ \ \int _0^{\infty} \cfrac{\cos \omega x}{a^2+\omega ^2}d\omega =\cfrac{\pi}{2a} e^{-ax} \]
$あらためて \quad x \longrightarrow t \quad , \omega \longrightarrow x \quad とおくと$
\[\int _0^{\infty} \cfrac{\cos tx}{a^2+x^2}dx =\cfrac{\pi}{2a} e^{-at} \quad なる定積分が得られます。\]
(ii)$\ \ x > 0\ のグラフを原点に関して対称にしたものを付加して奇関数に直すと$
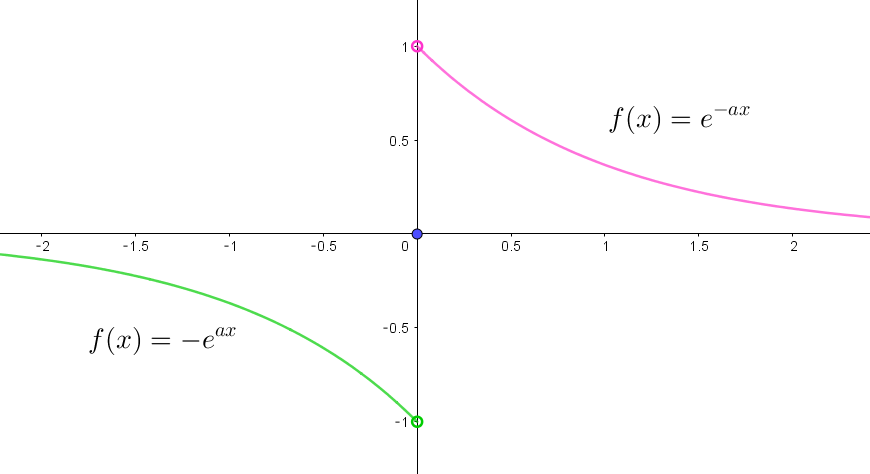
\[
f(x)=
\hspace{1em}
\left\{ \begin{array}{l}
-e^{ax} \quad ( x < 0)\\
0 \quad (x=0)\\
e^{-ax} \quad (x > 0 )\\
\end{array} \right.
\]
$逆変換は$
\[f(x)=\int _{-\infty}^{\infty} s(\omega)\sin \omega xd\omega = \int _0^{\infty} \cfrac{2\omega }{\pi(a^2+\omega ^2)}\sin \omega xd\omega\]
$これが \quad f(x)=e^{-ax} \quad に一致するから$
\[\int _0^{\infty} \cfrac{2\omega}{\pi(a^2+\omega ^2)}\sin \omega xd\omega=e^{-ax} \qquad \therefore \ \ \int _0^{\infty} \cfrac{\omega \cos \omega x}{a^2+\omega ^2}d\omega =\cfrac{\pi}{2} e^{-ax} \]
$あらためて \quad x \longrightarrow t \quad , \omega \longrightarrow x \quad とおくと$
\[\int _0^{\infty} \cfrac{x \sin tx}{a^2+x^2}dx =\cfrac{\pi}{2} e^{-at} \quad なる定積分が得られます。\]
フーリェ変換メニュー に戻る
メインメニュー に戻る