3 一般順位
$「X_{(k)} \leqq x \ \ である」ことは$
$X_1,X_2,\cdots , X_n \ \ のうち、「少なくともk個はx以下」すなわち 「x以下のものがk個以上」あることです。$
$そこで、「n個のうち、x以下のものがi個、xより大きいものがn-i個ある。」とすると、$
$その選び方は {}_n C _i 通りあるから$
\[P(X_{(k)} \leqq x)=\sum _{i=k}^n {}_n C_i \bigl(F(x)\bigr)^i\bigl(1-F(x)\bigr)^{n-i}\]
\[一般順位 \quad P(X_{(k)} \leqq x)=\sum _{i=k}^n {}_n C_i \bigl(F(x)\bigr)^i\bigl(1-F(x)\bigr)^{n-i}\]
(i)$Xが離散的な確率変数の場合$
$\quad X_{(k)}がxである確率 \ P(X_{(k)}=x) \ は$
\begin{eqnarray*} P(X_{(k)} =x) &=&P(X_{(k)} \leqq x)-P(X_{(k)} \leqq x-1)\\ &=&\sum _{i=k}^n {}_n C_i \bigl(F(x)\bigr)^i\bigl(1-F(x)\bigr)^{n-i}-\sum _{i=k}^n {}_n C_i \bigl(F(x-1)\bigr)^i\bigl(1-F(x-1)\bigr)^{n-i}\\ \end{eqnarray*}
\[Xが離散的な確率変数の場合\] \[\hspace{3em} P(X_{(k} =x)=\sum _{i=k}^n {}_n C_i \bigl(F(x)\bigr)^i\bigl(1-F(x)\bigr)^{n-i}-\sum _{i=k}^n {}_n C_i \bigl(F(x-1)\bigr)^i\bigl(1-F(x-1)\bigr)^{n-i}\]
$例5 \quad さいころをn回投げる。出た目を小さい順に並べたとき、下から2番目が2である確率$
$\quad 例1より \ \ P(X=x_i)=\cfrac{1}{6} \quad (i=1,2,\cdots,6),\ \ F(x)=\cfrac{x}{6},\ \ x=2 \ \ だから$
\begin{eqnarray*} P(X_{(2)}=2) &=&\sum _{i=2}^n {}_n C_i \bigl(\cfrac{2}{6}\bigr)^i\bigl(1-\cfrac{2}{6}\bigr)^{n-i}-\sum _{i=2}^n {}_n C_i \bigl(\cfrac{1}{6}\bigr)^i\bigl(1-\cfrac{1}{6}\bigr)^{n-i}\\ &=&1-{}_n C_0 \bigl(\cfrac{2}{3}\bigr)^n-{}_n C_1 \bigl(\cfrac{1}{3}\bigr)\bigl(\cfrac{2}{3}\bigr)^{n-1} -\bigl\{1-{}_n C_0 \bigl(\cfrac{5}{6}\bigr)^n-{}_n C_1 \bigl(\cfrac{1}{6}\bigr)\bigl(\cfrac{5}{6}\bigr)^{n-1}\bigr\}\\ &=&\bigl(\cfrac{5}{6}\bigr)^n+ n\bigl(\cfrac{1}{6}\bigr)\bigl(\cfrac{5}{6}\bigr)^{n-1} -\bigl(\cfrac{2}{3}\bigr)^n- n\bigl(\cfrac{1}{3}\bigr)\bigl(\cfrac{2}{3}\bigr)^{n-1}\\ \end{eqnarray*}
(ii)$Xが連続的な確率変数の場合$
$\quad Xの確率密度関数をf(x)、分布関数をF=F(x)とし、X_{(k)}の確率密度関数をf_{(k)}(x)とする。$
$\quad 連続な場合、分布関数の導関数が確率密度関数となるから$
\begin{eqnarray*} P(X_{(k)} \leqq x) &=&\sum _{i=k}^n {}_n C_i F^i(1-F)^{n-i}\\ &=&{}_n C_k F^k(1-F)^{n-k}+{}_n C_{k+1} F^{k+1}(1-F)^{n-k-1}+\cdots +{}_n C_n F^n\\ \end{eqnarray*} $両辺をxで微分して$
\begin{eqnarray*} f_{(k)}(x) &=&k{}_n C_k fF^{k-1}(1-F)^{n-k}-(n-k){}_n C_k fF^k(1-F)^{n-k-1}\hspace{16em}(1)\\ \\ &+&(k+1){}_n C_{k+1} fF^k(1-F)^{n-k-1}-(n-k-1){}_n C_{k+1} fF^{k+1}(1-F)^{n-k-2}\hspace{10em}(2)\\ \\ &+&(k+2){}_n C_{k+2} fF^{k+1}(1-F)^{n-k-2}-(n-k-2){}_n C_{k+2} fF^{k+2}(1-F)^{n-k-3}\hspace{9em}(3)\\ \\ &&\hspace{5em}\vdots \\ \\ &+&n{}_n C_n fF^{n-1}\\ \end{eqnarray*} $(2)式の1項めと(1)式の2項めは同類項でその係数は$
$\hspace{3em}(k+1){}_n C_{k+1} -(n-k){}_n C_k $
\begin{eqnarray*} &=&\cfrac{(k+1)n!}{(k+1)!(n-k-1)!}-\cfrac{(n-k)n!}{k!(n-k)!}\\ \\ &=&\cfrac{n!}{k!(n-k-1)!}-\cfrac{n!}{k!(n-k-1)!}\\ \\ &=&0\\ \end{eqnarray*} $斜めにある他の同類項も同じように消去されて(1)式の1項めだけ残るから$
\begin{eqnarray*} f_{(k)}(x) &=&k{}_n C_k fF^{k-1}(1-F)^{n-k}\\ \\ &=&\cfrac{kn!}{k!(n-k)!}fF^{k-1}(1-F)^{n-k}\\ \\ &=&\cfrac{n!}{(k-1)!(n-k)!}fF^{k-1}(1-F)^{n-k}\\ \\ &=&\cfrac{n(n-1)!}{(k-1)!\{(n-1)-(k-1)\}!}fF^{k-1}(1-F)^{n-k}\\ \\ &=&n \ {}_{n-1} C_{k-1} fF^{k-1}(1-F)^{n-k}\\ \end{eqnarray*}
$\qquad Xが連続的な確率変数の場合 \quad f_{(k)}(x)=n \ {}_{n-1} C_{k-1} fF^{k-1}(1-F)^{n-k}$
$例6 [0,1]の一様乱数をn個とり、u_1,u_2,\cdots ,u_nとする。確率密度関数 \ f_{(k)}(x) \ を求めてみましょう。$
\[f(x)= \left\{ \begin{array}{l} 0 \hspace{3em} (x < 0,x > 1 )\\ 1 \hspace{3em} (0 \leqq x \leqq 1)\\ \end{array} \right. \] $だから f(x)の分布関数は$
\[F(x)=\int _{-\infty}^{x} f(x)dx=\int _{0}^{x} dx=x\]
 $したがって f_{(k)}(x)=n \ {}_{n-1} C_{k-1} x^{k-1}(1-x)^{n-k} \quad (\ 0 \leqq x \leqq 1 \ ) $
$したがって f_{(k)}(x)=n \ {}_{n-1} C_{k-1} x^{k-1}(1-x)^{n-k} \quad (\ 0 \leqq x \leqq 1 \ ) $
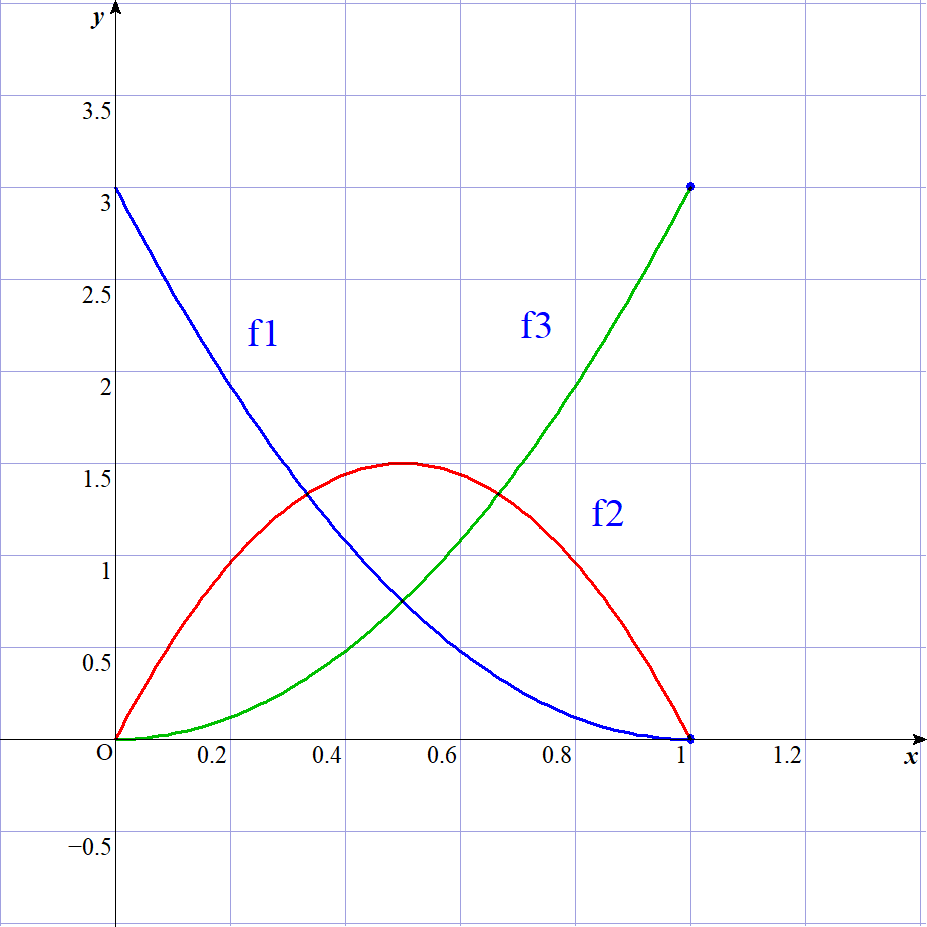
$n=3 のときのすべての順位統計量の式とそのグラフは$
$\quad f_{(1)}(x)=3{}_{2} C_{0} x^{0}(1-x)^{2}=3(1-x)^2$
$\quad f_{(2)}(x)=3{}_{2} C_{1} x^{1}(1-x)^{1}=6x(1-x)$
$\quad f_{(3)}(x)=3{}_{2} C_{2} x^{2}(1-x)^{0}=3x^2$
$\quad f_{(1)}とf_{(2)}のグラフは直線 \ x=\cfrac{1}{2} \ に関して対称です。$
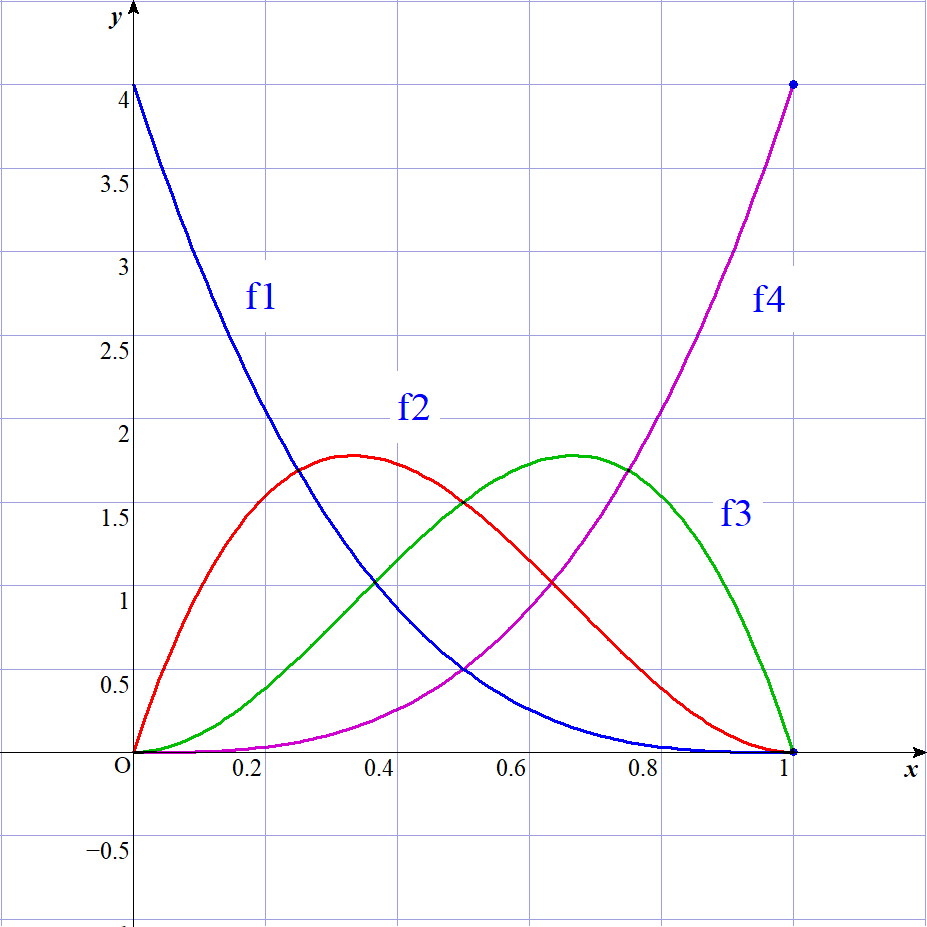
$n=4 のときのすべての順位統計量の式とそのグラフは$
$\quad f_{(1)}(x)=4{}_{3} C_{0} x^{0}(1-x)^{3}=4(1-x)^3$
$\quad f_{(2)}(x)=4{}_{3} C_{1} x^{1}(1-x)^{2}=12x(1-x)^2$
$\quad f_{(3)}(x)=4{}_{3} C_{2} x^{2}(1-x)^{1}=12x^2(1-x)$
$\quad f_{(4)}(x)=4{}_{3} C_{3} x^{3}(1-x)^{0}=4x^3$
$\quad f_{(1)}とf_{(4)}のグラフ \ および \ f_{(2)}とf_{(3)}のグラフは$
$それぞれ直線 \ x=\cfrac{1}{2} \ に関して対称です。$
順位統計量メニュー に戻る