MY MATH NOTE

九州大学(理系) 2018年　問題2

$原点を中心とする半径 \ 3\ の半円 \ C:x^2+y^2=9 \ \ ( y \geqq 0)\ 上の \ 2\ 点 \ P\ と \ Q\ に対し、線分 \ PQ\ を 2:1\ に$
$内分する点を \ R\ とする。以下の問いに答えよ。$
$(1)\ \ 点 \ P\ の \ y\ 座標と \ Q\ の \ y\ 座標が等しく、かつ \ P\ の \ x\ 座標は \ Q\ の \ x\ 座標より小さくなるように$
$\quad P\ と \ Q\ が動くものとする。このとき、線分 \ PR\ が通過してできる図形 \ S\ の面積を求めよ。$
$(2)\ \ 点 \ P\ を \ (-3,\ 0)\ に固定する。Q\ が半円 \ C\ 上を動くとき線分 \ PR\ が通過してできる図形 \ T\ の面積を求めよ。$
$(3)\ \ (1)の図形 \ S\ から(2)の図形 \ T\ を除いた図形と第 \ 1\ 象限の共通部分を \ U\ とする。U\ を \ y\ 軸のまわりに$
$\quad 1\ 回転させてできる回転体の体積を求めよ。$

(1)

　
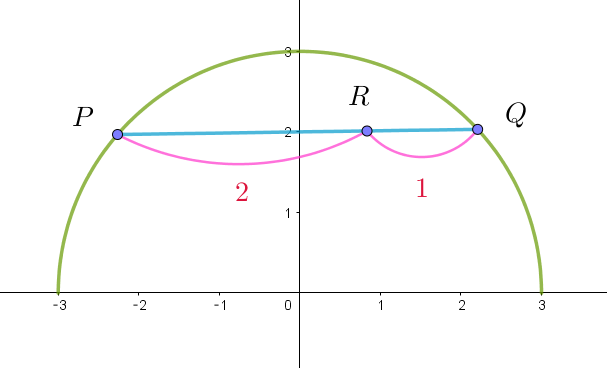
$点 \ P(-t,\ u),\ Q(t,\ u) \ とおくと \ R(x,\ y)\ は$

$\quad x=\cfrac{-t+2t}{3}=\cfrac{t}{3},\qquad y=u$

$よって \qquad t=3x,\quad u=y$

$Q(t,\ u)\ は \quad t^2 + u^2=9 \ \ (u \geqq 0)\ \ を満たすから$

　
$\quad (3x)^2 + y^2=9 \qquad \therefore \ \ x^2+\cfrac{y^2}{9}=1 \ \ (y \geqq 0)$

$よって \quad R(x,\ y)\ の軌跡は楕円である。$

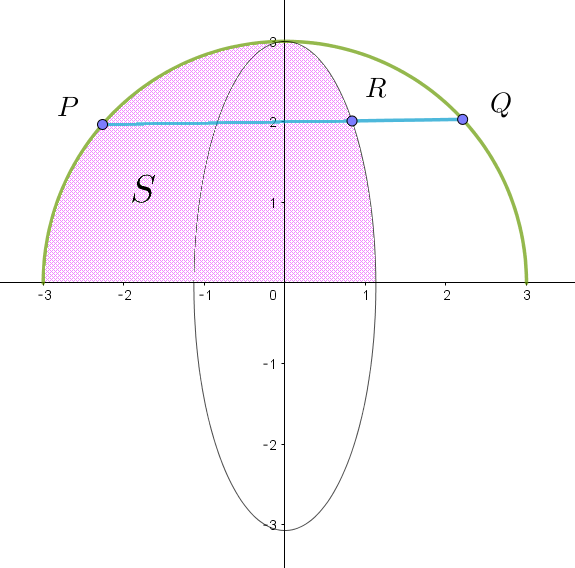
$線分 \ PR\ が通過してできる図形 \ S\ は右図のとおりである。$

$\quad S=\cfrac{1}{4}\times \pi \times 3^2+\cfrac{1}{4} \times \pi \times 1 \times 3=3\pi$

$なお、楕円の面積については($楕円$)を参考にしてください。$

(2)

　
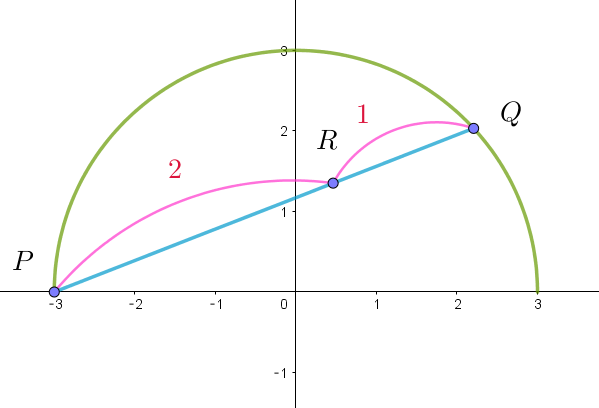
$点 \ P(-3,\ 0),\ Q(t,\ u) \ とおくと \ R(x,\ y)\ は$

$\quad x=\cfrac{-3+2t}{3},\qquad y=\cfrac{2u}{3}$

$よって \quad t=\cfrac{3}{2}(x+1),\quad u=\cfrac{3}{2}y$

$Q(t,\ u)\ は \quad t^2+u^2=9 \ \ (u \geqq 0)\ \ を満たすから$

$\quad \cfrac{9}{4}(x+1)^2 + \cfrac{9}{4}y^2=9 \qquad \therefore \ \ (x+1)^2+y^2=4 \ \ (y \geqq 0)$

$よって \quad R(x,\ y)\ の軌跡は、中心 \ (-1,\ 0),\ \ 半径 \ 2\ の円である。$

　
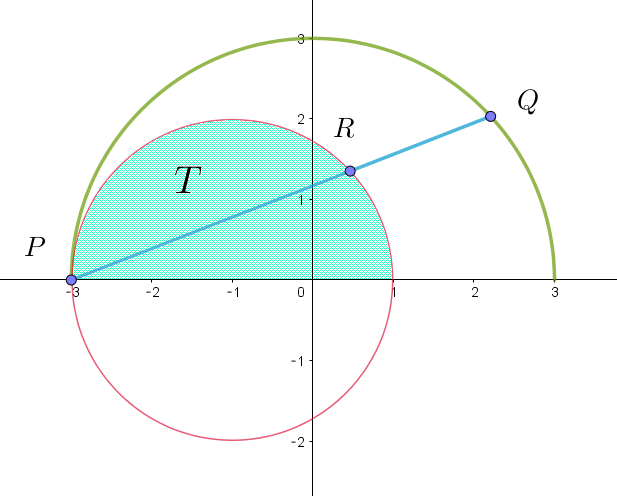
$線分 \ PR\ が通過してできる図形 \ T\ は右図のとおりである。$

$\quad T=\cfrac{1}{2}\times \pi \times 2^2=2\pi$

(3)

　
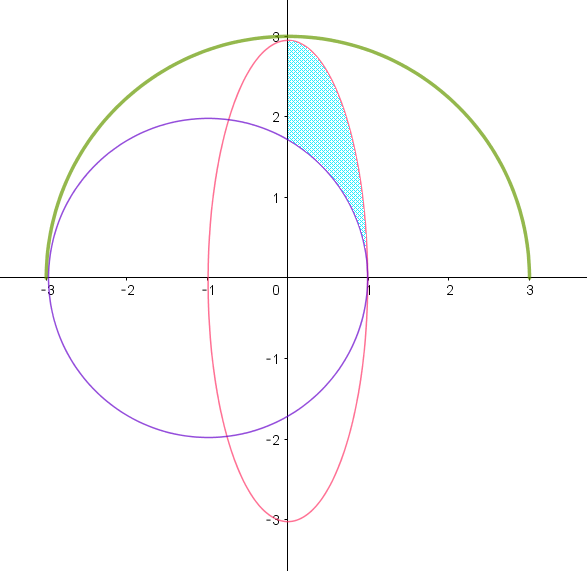
$図形 \ U\ は右のとおり、求める体積をVとすると$
\[V=\pi\int _0^3(1-\cfrac{y^2}{9})dy-\pi\int _0^{\sqrt{3}}(\sqrt{4-y^2}-1)^2dy\] $\qquad 第1項=\pi\big[y-\cfrac{y^3}{27}\big]_0^3=2\pi$

\begin{eqnarray*} 第2項 &=&\pi\int _0^{\sqrt{3}}(4-y^2-2\sqrt{4-y^2}+1)dy\\ \\ &=&\pi\big[5y-\cfrac{y^3}{3}\big] _0^{\sqrt{3}}-2\pi\int _0^{\sqrt{3}}\sqrt{4-y^2}dy\\ \\ &=&4\sqrt{3}\pi -2\pi\int _0^{\sqrt{3}}\sqrt{4-y^2}dy\\ \end{eqnarray*} \[ここで \quad I=\int _0^{\sqrt{3}}\sqrt{4-y^2}dy \quad は\] $\hspace{3em} y=2\sin \theta \quad とおくと \qquad dy=2\cos \theta d\theta $
\[ \quad \begin{array}{c|c} y & \ \ \ 0\ \ \rightarrow \sqrt{3} \quad \\ \hline \theta & 0\ \ \rightarrow \cfrac{\pi}{3} \\ \end{array} \] \begin{eqnarray*} I &=&\int _0^{\small{\cfrac{\pi}{3}}}\sqrt{4(1-\sin ^2 \theta)}\cdot 2 \cos \theta d\theta\\ &=&4\int _0^{\small{\cfrac{\pi}{3}}}\cos ^2\theta d\theta\\ &=&2\int _0^{\small{\cfrac{\pi}{3}}}(1+\cos 2\theta) d\theta\\ &=&2\big[\theta +\cfrac{1}{2}\sin 2\theta \big]_0^{\small{\cfrac{\pi}{3}}} \\ &=&2\big(\cfrac{\pi}{3}+\cfrac{1}{2}\sin \cfrac{2\pi}{3}\big)\\ &=&\cfrac{2}{3}\pi+\cfrac{\sqrt{3}}{2}\\ \end{eqnarray*} $第2項=4\sqrt{3}\pi -2\pi\big(\cfrac{2}{3}\pi+\cfrac{\sqrt{3}}{2}\big)=3\sqrt{3}\pi -\cfrac{4}{3}\pi^2$

$よって \qquad V=2\pi-\big(3\sqrt{3}\pi -\cfrac{4}{3}\pi^2\big)=(2-3\sqrt{3})\pi+\cfrac{4}{3}\pi^2$

ページの先頭へ↑