楕円

　

１　定義1


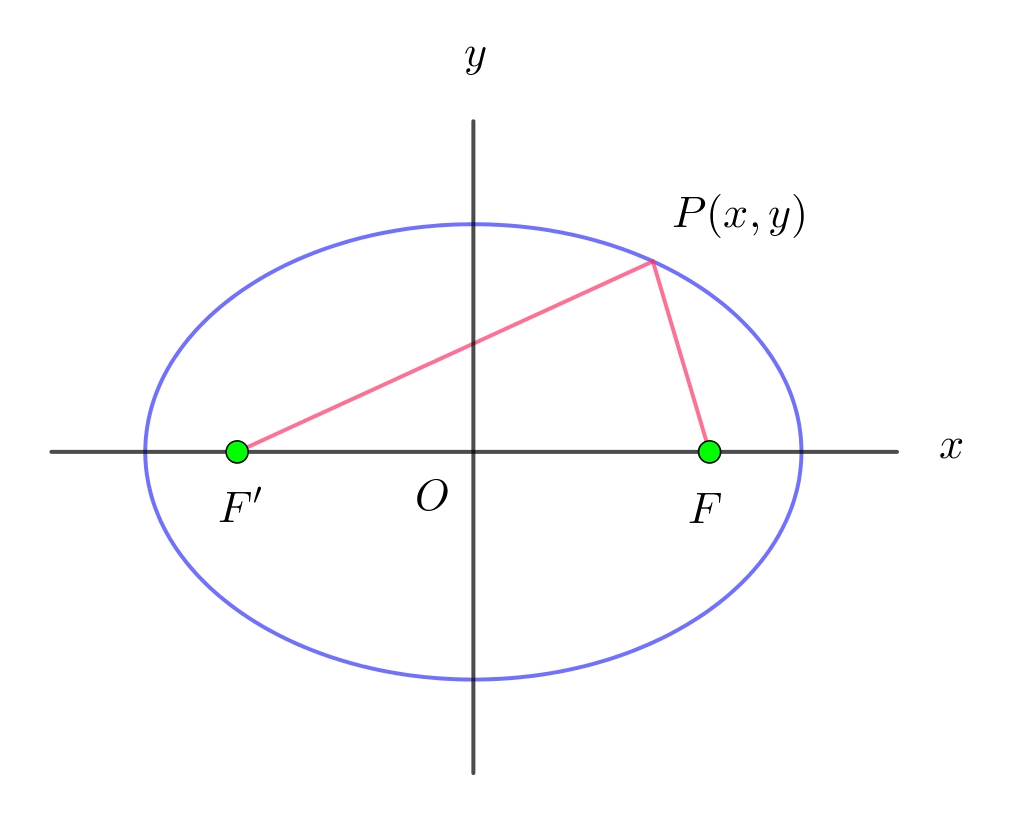
$平面上で、2定点からの距離の和が一定な点の軌跡を楕円$
$といいます。$

$2定点をF,F'とし、この2点を通る直線をx軸、線分FF'の$
$垂直二等分線をy軸とする。$
$c>0\ \ として、F(c,0),\ \ F'(-c,0),\ \ P(x,y) 　とする。$
$PF+PF'=2a \quad (aは正の定数)とおくと$

$\sqrt{(x-c)^2+y^2)}+\sqrt{(x+c)^2+y^2)}=2a$

$\sqrt{(x+c)^2+y^2)}=2a-\sqrt{(x-c)^2+y^2)}$

$両辺を平方して$

$(x+c)^2+y^2 = 4a^2-4a\sqrt{(x-c)^2+y^2)}+(x-c)^2+y^2$

$a\sqrt{(x-c)^2+y^2)}=a^2-cx \hspace{10em}(1)$

$\sqrt{(x-c)^2+y^2)}=\cfrac{c}{a}\big(\cfrac{a^2}{c}-x\big)$

　

$\cfrac{c}{a}=e 　とおくと　\cfrac{a^2}{c}=\cfrac{a}{e} 　だから$

$\sqrt{(x-c)^2+y^2)}=e\big(\cfrac{a}{e}-x\big) \hspace{10em} (2)$

$左辺は正であるから、x < \cfrac{a}{e}$
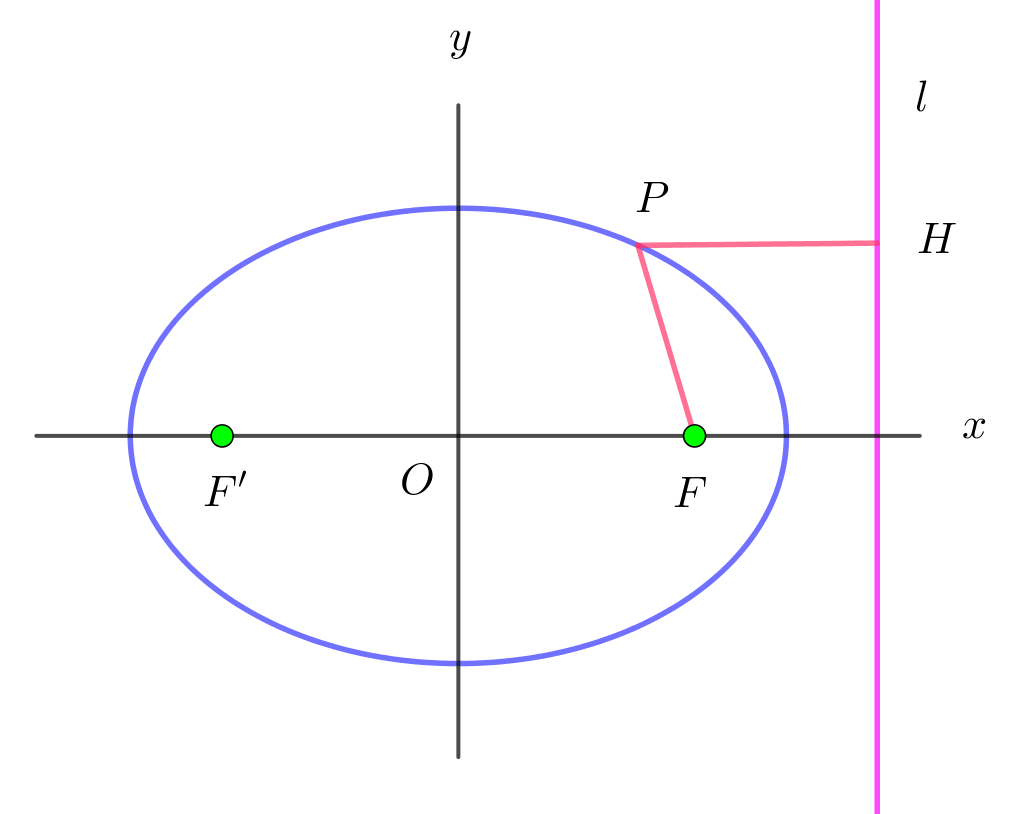
$また、左辺は線分PFの長さで、右辺は点P(x,y)\ \ から$
$直線\ l: x=\cfrac{a}{e}\ \ に下ろした垂線の長さPHのe倍である。$
$よって　\ \ PF=ePH $

$さらに(1)の両辺を平方して$

$a^2\{(x-c)^2+y^2\}=(a^2-cx)^2$

$(a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)$

$ここで、△PF'Fにおいて \quad PF+PF'>FF' \ \ より$

$\qquad ($ 三角形の辺と角をめぐる基本定理$を参考にしてください)$

$\qquad 2a > 2c \qquad \therefore a > c$

　 $したがって \quad \cfrac{x^2}{a^2}+\cfrac{y^2}{a^2-c^2}=1$

$a^2-c^2=b^2\quad (b>0) とおくと$

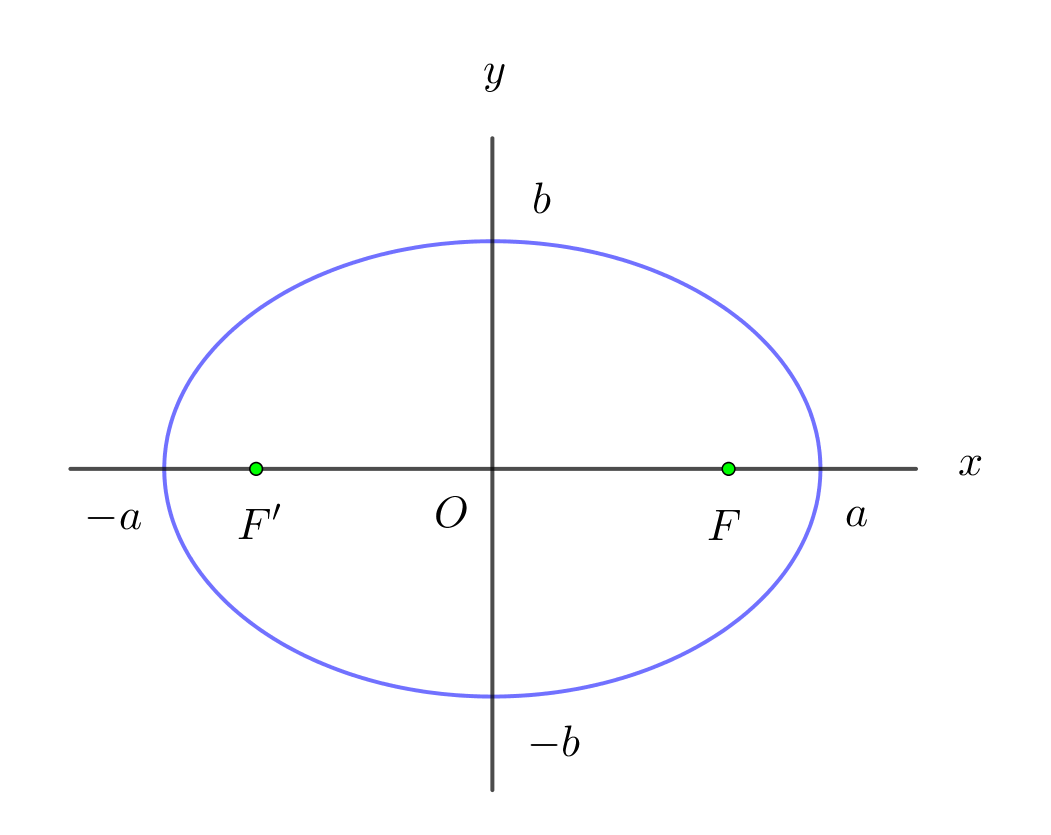
$\quad \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1$

$これが楕円の方程式で、グラフは右図のとおりです。$

$なお、a^2=b^2+c^2 　だから　 a>b$

$\quad e=\cfrac{c}{a}=\cfrac{\sqrt{a^2-b^2}}{a}$

$F(c,0)とF'(-c,0) を焦点、e\ \ を離心率、直線 \ \ x=\cfrac{a}{e} 　を準線といいます。$

$e=\cfrac{c}{a} 　で　 a > c 　だから　 0 < e < 1$


2　PF,PF'の長さ


$\quad 1の(2)より$

$\qquad PF=\sqrt{(x-c)^2+y^2}=e(\cfrac{a}{e}-x)=a-ex$

$\quad 定義から \quad PF+PF'=2a \quad だから$

$\qquad PF'=2a-PF=2a-(a-ex)=a+ex$


3　定義 2

　

$上のことから、定点Fと定直線lへの距離の比が$

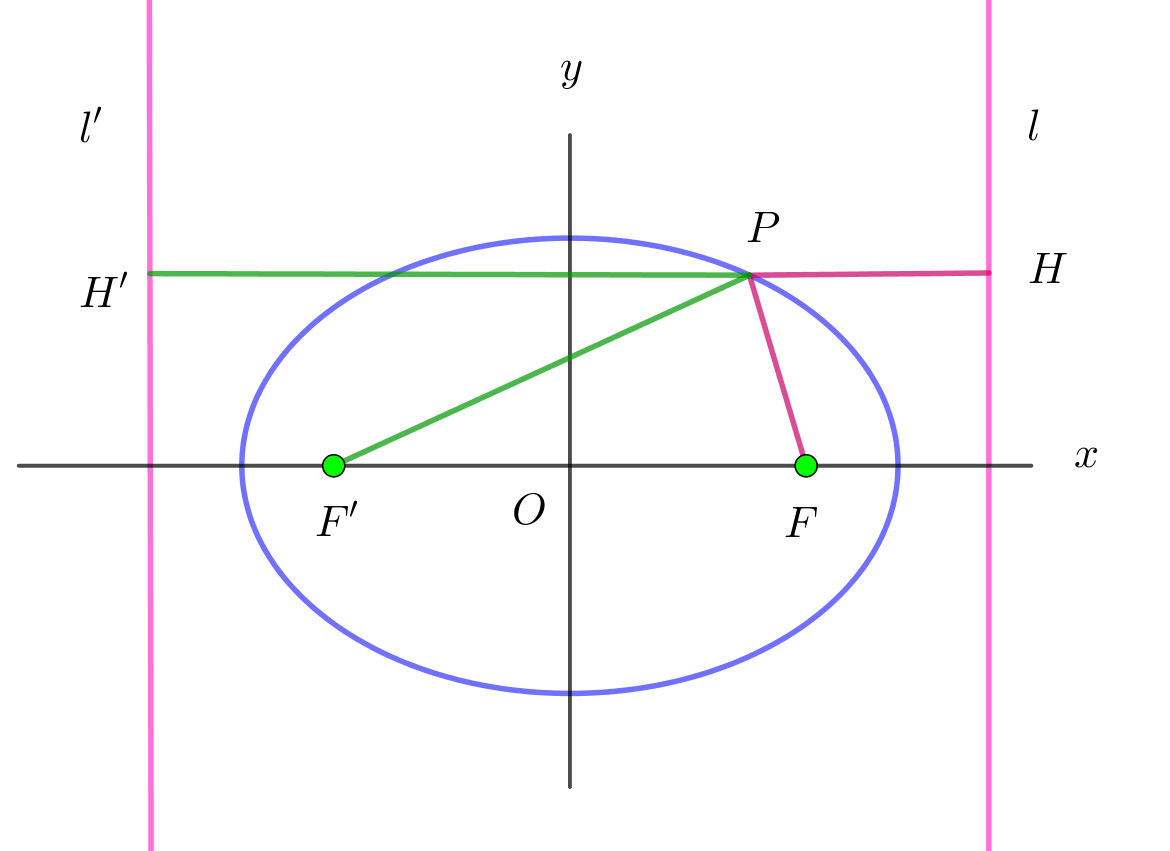
$\quad PF:PH=e:1 \quad (0 < e <1)$

$\ \ である点Pの軌跡を楕円という$

$といってもよいでしょう。$

$これを定義とした場合、楕円がy軸について対称で$
$あることから$
$\quad F'(-c,0) \quad 準線を\ \ l':x=-\cfrac{a}{e} 　でとると$
$\quad PF+PF'=ePH+ePH'=e(\cfrac{a}{e}-x)+e(x+\cfrac{a}{e})=2a$
$となり、定義1が導かれます。$

$したがって、定義1と定義2のどちらをとっても同じです。$


4　楕円の極座標表示

　

$点Fを原点、x軸の正方向を始線とする極座標で表し$
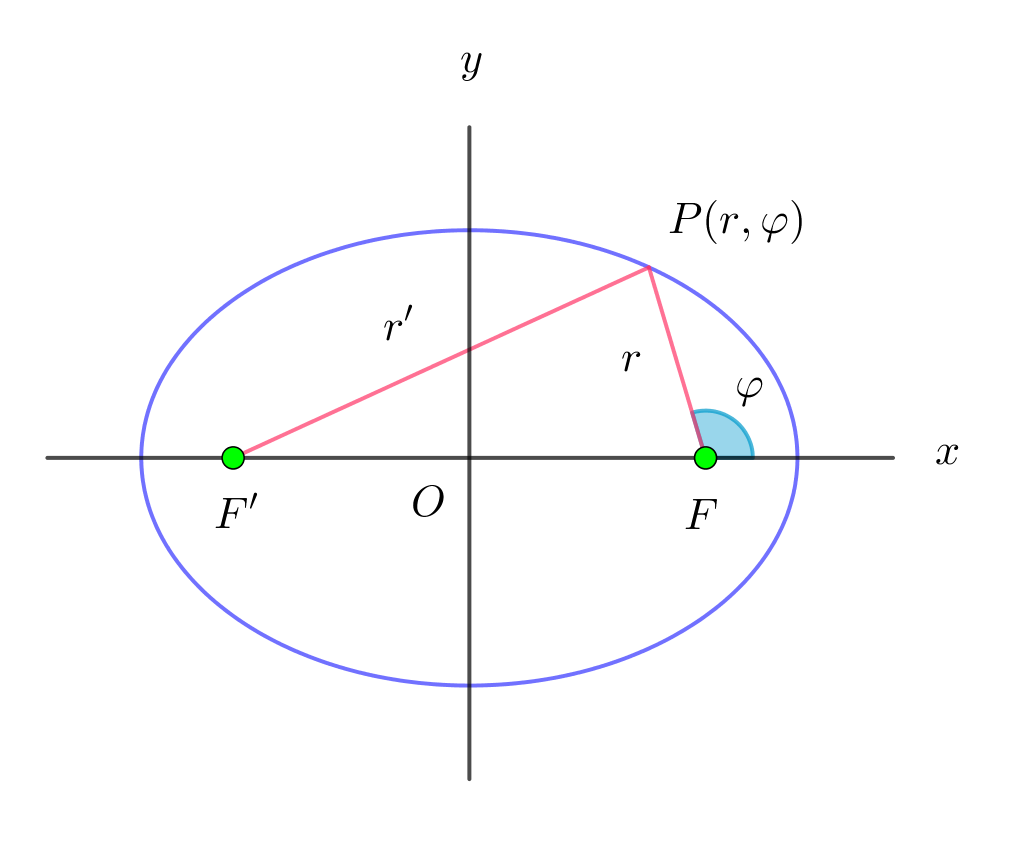
$ましょう。$

$右図のように、P(r,\varphi),\quad PF'=r' \ \ とすると$
$△PF'Fに余弦定理を用いて$

$\quad r'^2=r^2+(2c)^2-2r(2c)\cos(\pi-\varphi)$

$\quad r+r'=2a,\quad c^2=a^2-b^2 を代入して$

$\quad (2a-r)^2=r^2+4(a^2-b^2)+4rc\cos \varphi $

$\quad r(a+c\cos \varphi )=b^2$

$\quad r=\cfrac{b^2}{a+c\cos \varphi}=\cfrac{\cfrac{b^2}{a}}{1+\cfrac{c}{a}\cos \varphi}$

$ここで、\cfrac{c}{a}=e,\quad \cfrac{b^2}{a}=l 　とおくと \quad r=\cfrac{l}{1+e\cos \varphi}$

$なお、\varphi =\cfrac{\pi}{2} のとき　r=l \ \ となるが、準線を表すlではないので注意してください。$


$極座標を利用した性質(問題)が多くありますが、とりあえず省略します。$


5　楕円の媒介変数表示


$(1)三角関数を用いた表示$

　

$円　x^2+y^2=a^2 \ \ 上の点P(x,y)をy軸方向に\ \ \cfrac{b}{a} 倍に$
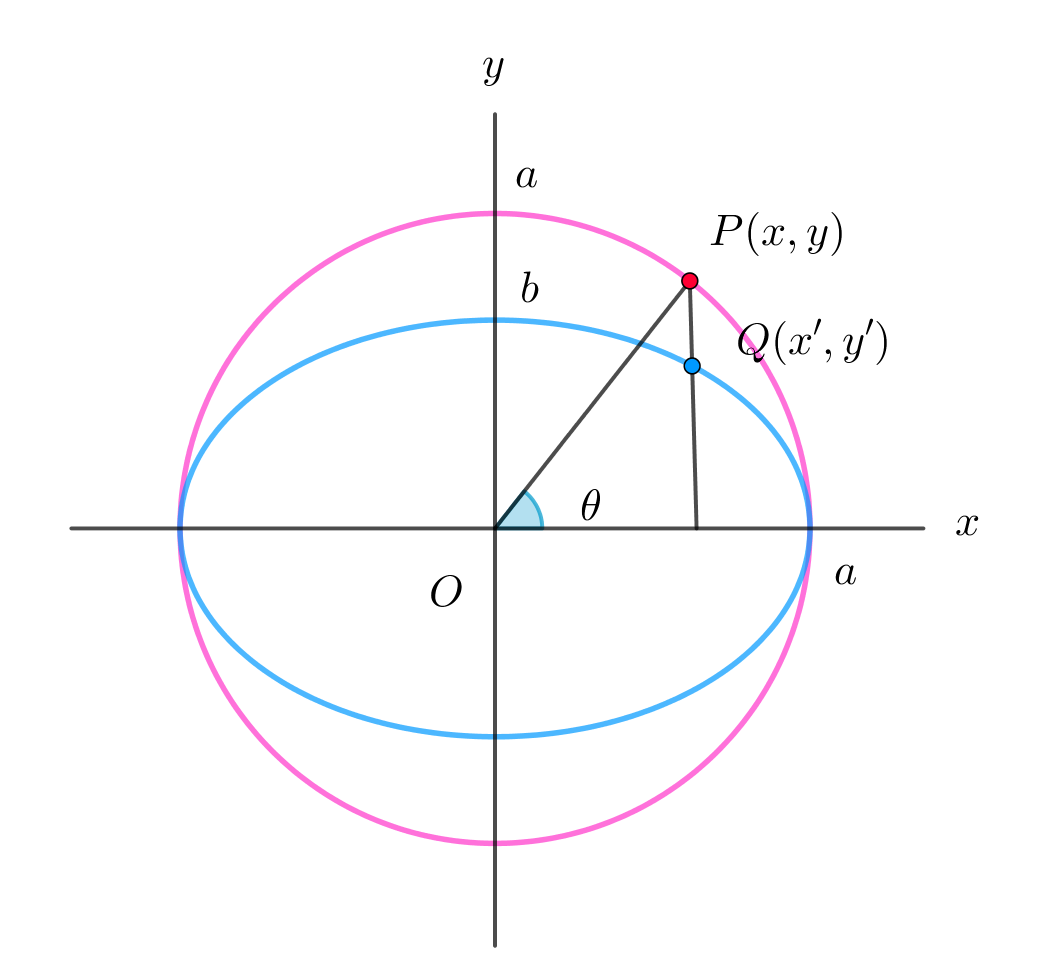
$縮小した点をQ(x',y')とすると$

$\quad x'=x,\quad y'=\cfrac{b}{a}y 　だから$
$\quad x=x',\quad y=\cfrac{a}{b}y' \ \ を　 x^2+y^2=a^2 　に代入して$
$\quad x'^2+\cfrac{a^2}{b^2}y'^2=a^2$

$\quad \cfrac{x'^2}{a^2}+\cfrac{y'^2}{b^2}=1$

$x',y' をあらためて　x,y と表すと　楕円　\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1 　がえられる。$

$このように、円をx軸方向に縮小したものを楕円といってもよいが、これを定義としても$
$焦点、離心率、準線などが得られません。$

$線分OPとx軸の正方向のなす角を\theta とすると$

$\quad x=a\cos \theta, \quad y=a\sin \theta 　は円の媒介変数表示である。$

$円　x^2+y^2=a^2 \ \ 上の点P(x,y)をy軸方向に \ \cfrac{b}{a} 倍に縮小した点 \ Q(x,y)は$
$楕円　\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1 　上の点であるから$
$\quad x=a\cos \theta, \quad y=b\sin \theta 　が楕円の媒介変数表示である。$


$(2)有理関数を用いた表示$

　

$楕円　\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1 　と点(-a,0) を通る傾きtの$
$直線 \ \ y=t(x+a) の交点は$
\[ \left\{ \begin{array}{l} \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\\ \ \ y=t(x+a)\\ \end{array} \right. \] $\quad b^2x^2+a^2t^2(x+a)^2=a^2b^2$
$\quad b^2(x^2-a^2)+a^2t^2(x+a)^2=0$
$\quad (x+a)\{b^2(x-a)+a^2t^2(x+a)\}=0$
$\quad x \ne -a \ \ より \quad b^2(x-a)+a^2t^2(x+a)=0$
$\quad (b^2+a^2t^2)x+a^3t^2-ab^2=0$

$\quad \therefore x=\cfrac{a(b^2-a^2t^2)}{b^2+a^2t^2}$

$\quad y=t\big(\cfrac{a(b^2-a^2t^2)}{b^2+a^2t^2}+a\big)=\cfrac{2ab^2t}{b^2+a^2t^2}$

$これがtを媒介変数とした、楕円の有理関数表示です。$

$ただし、点(-a,0)は表せません。(t \rightarrow \infty の場合ですが)$


6　楕円の囲む面積


$\quad \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1 　より　y^2=b^2\big(1-\cfrac{x^2}{a^2}\big)=\cfrac{b^2}{a^2}(a^2-x^2)$

$\quad \therefore y=\cfrac{b}{a}\sqrt{a^2-x^2}$
\[求める面積は　S=4 \times \cfrac{b}{a}\int _0 ^a \sqrt{a^2-x^2}dx\] $積分は四分円の面積だから　 S=4\times \cfrac{b}{a} \times \cfrac{1}{4}\pi a^2=\pi ab$


7　楕円の弧長


$楕円の媒介変数表示は \quad x=a\cos \theta, \quad y=b\sin \theta 　だから微小な長さ(線素)は$
\begin{eqnarray*} ds&=&\sqrt{\big(\cfrac{dx}{d\theta}\big)^2+\big(\cfrac{dy}{d\theta}\big)^2} d\theta\\ \\ &=&\sqrt{(-a\sin \theta )^2+(b\cos \theta )^2}\ d\theta\\ \\ &=&\sqrt{a^2\sin ^2 \theta +b^2\cos ^2 \theta }\ d\theta\\ \end{eqnarray*} $したがって、楕円の弧長は$
\[L=4\int _0 ^\cfrac{\pi}{2}\sqrt{a^2\sin ^2 \theta +b^2\cos ^2 \theta }\ d\theta \] $となります。$

$これは第2種楕円積分に変形できますが、詳しくは$　J(a,b)のページ　$をご覧ください)$



ページの先頭へ↑



2次曲線メニュー　に戻る


メインメニュー　に戻る