早稲田大学(理系) 2024年 問題Ⅰ
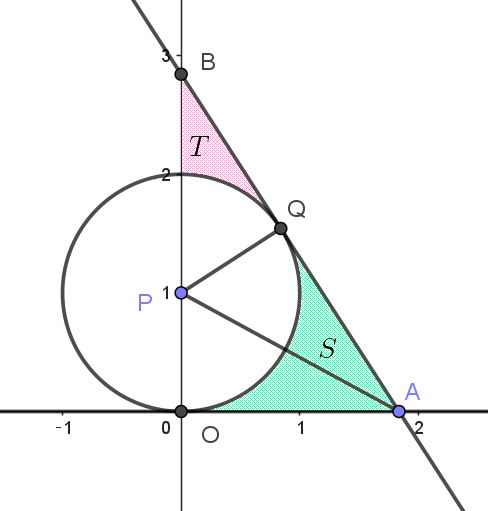
$円 \ C:x^2+(y-1)^2=1 \ に接する直線で、x\ 切片、y\ 切片がともに正であるものを \ \ell \ とする。C\ と \ \ell \ と$
$x\ 軸により囲まれた部分の面積を \ S、C\ と \ \ell \ と \ y\ 軸により囲まれた部分の面積を \ T\ とする。S+T\ が$
$最小となるとき、S-T\ の値を求めよ。$

$それぞれ \ A,\ \ B\ \ とおく。$
$\triangle OAP \ \ と \ \ \triangle QAP \ \ において$
$円の接線の性質から \quad PO \perp AO,\quad PQ \perp AQ$
$\quad (このことについては($円の接線$)をご覧ください。)$
$PO=PQ=1,\quad PA \ \ は共通だから \qquad \triangle OAP \equiv \triangle QAP $
$よって \quad \angle OAQ=\angle QAP$
$接線 \ \ \ell \ \ のパラメータとして \quad \angle OAQ=\angle QAP=\theta \quad とおく。$
$0< 2\theta < \cfrac{\pi}{2} \quad だから \quad 0 < \theta < \cfrac{\pi}{4}$
$OA=a,\ \ OB=b\ \ (a > 0,\ b > 0)\ \ とおくと \quad \triangle OAP \ \ において \quad \tan \theta=\cfrac{OP}{OA}=\cfrac{1}{a}$
$\therefore \ \ a=\cfrac{1}{\tan \theta}$
$\triangle OAB において \quad \tan 2\theta=\cfrac{OB}{OA}=\cfrac{b}{a}$
$\therefore \ \ b=a\tan 2\theta=\cfrac{\tan 2\theta}{\tan \theta}$
$S+T \ \ が最小になるときは、円 \ C\ の面積は一定だから$
$\triangle OAB=\cfrac{1}{2}ab \quad が最小のときである。$
\begin{eqnarray*} \cfrac{1}{2}ab &=&\cfrac{1}{2}\times \cfrac{1}{\tan \theta} \times \cfrac{\tan 2\theta}{\tan \theta}\\ \\ &=&\cfrac{\tan \theta}{\tan ^2\theta (1-\tan ^2\theta)}\\ \\ &=&\cfrac{1}{\tan \theta (1-\tan ^2\theta)} \end{eqnarray*}
$t=\tan \theta \quad とおくと \quad f(t)=t(1-t^2) =t-t^3 \quad が最大となればよい。$
$ただし、 0 < \theta < \cfrac{\pi}{4} \quad より \quad 0 < t < 1$
$f'(t)=1-3t^2$
$f'(t)=0 \quad より \quad t=\cfrac{1}{\sqrt{3}}$
$増減表$
\[ \begin{array}{c||c|c|c|c|c} t& 0 & \cdots & \dfrac{1}{\sqrt{3}} & \cdots & 1\\ \hline f'(t)& & + & 0 & - & \\ \hline f(t)& & \nearrow & 極大 & \searrow & \\ \end{array} \]
$t=\cfrac{1}{\sqrt{3}}\ で \ f(t)\ は極大かつ最大となる。$
$t=\tan \theta =\cfrac{1}{\sqrt{3}} \quad より \quad \theta=\cfrac{\pi}{6}$
$このとき$
$a=\cfrac{1}{\tan \dfrac{\pi}{6}}=\sqrt{3}$
$\angle OPQ=\pi - \angle OAQ=\pi - 2\theta=\cfrac{2}{3}\pi \quad だから$
\begin{eqnarray*} S &=&2\triangle OAP - \cfrac{1}{3} \times (円Cの面積)\\ \\ &=&2 \times \cfrac{1}{2} \times \sqrt{3} \times 1- \cfrac{1}{3} \times \pi \times 1^2\\ \\ &=&\sqrt{3}-\cfrac{\pi}{3} \end{eqnarray*}
$また$
$b=a\tan \cfrac{\pi}{3} = \sqrt{3} \times \sqrt{3}=3$
$PB=OB-OP=b-1=2,\qquad BQ=PQ\tan (\pi -\cfrac{2}{3}\pi)=\tan \cfrac{\pi}{3}=\sqrt{3}$
\begin{eqnarray*} T &=&\triangle BPQ - \cfrac{1}{6} \times (円Cの面積)\\ \\ &=&\cfrac{1}{2} \times 1 \times \sqrt{3} - \cfrac{1}{6} \times \pi \times 1^2\\ \\ &=&\cfrac{\sqrt{3}}{2}-\cfrac{\pi}{6} \end{eqnarray*} $よって \quad S+T\ \ が最小になるとき、S-T=(\sqrt{3}-\cfrac{\pi}{3})-(\cfrac{\sqrt{3}}{2}-\cfrac{\pi}{6})=\cfrac{\sqrt{3}}{2}-\cfrac{\pi}{6}$
$(別解)$
$接線 \ \ell \ のパラメータとして、 傾きを \ m\ とする。$
$円 \ C: x^2+(y-1)^2=1 \ \ と \ \ \ell : y=mx+n \ \ (m < 0)\ \ が接する条件は$
$x^2+(mx+n-1)^2=1$
$(m^2+1)x^2+2m(n-1)x+(n-1)^2-1=0$
$\cfrac{D}{4}=m^2(n-1)^2-(m^2+1)((n-1)^2-1)=0$
$m^2-(n-1)^2+1=0$
$(n-1)^2=m^2+1$
$n > 1 \ \ だから \quad n=1+\sqrt{m^2+1}$
$したがって \quad \ell : y=mx + 1+\sqrt{m^2+1}$
$よって \quad A(-\cfrac{1+\sqrt{m^2+1}}{m},\ 0), \quad B(0,\ 1+\sqrt{m^2+1})$
$\triangle OAB=\cfrac{1}{2} \times \big(-\cfrac{1+\sqrt{m^2+1}}{m}\big) \times (1+\sqrt{m^2+1})=-\cfrac{1}{2} \cdot \cfrac{(1+\sqrt{m^2+1})^2}{m}$
$f(m)=\cfrac{(1+\sqrt{m^2+1})^2}{m} \quad とおくと$
\begin{eqnarray*} f'(m) &=&\cfrac{2(1+\sqrt{m^2+1}) \times \dfrac{m}{\sqrt{m^2+1}} \times m -(1+\sqrt{m^2+1})^2 }{m^2}\\ \\ &=&\cfrac{2m^2(1+\sqrt{m^2+1})-(1+\sqrt{m^2+1})^2\sqrt{m^2+1}}{m^2\sqrt{m^2+1}}\\ \\ &=&\cfrac{(1+\sqrt{m^2+1})\{2m^2 -(1+\sqrt{m^2+1})\sqrt{m^2+1}\}} {m^2\sqrt{m^2+1}}\\ \\ &=&\cfrac{(1+\sqrt{m^2+1})(m^2-1 -\sqrt{m^2+1)}}{m^2\sqrt{m^2+1}}\\ \end{eqnarray*} $f'(m)=0 \ \ より$
$m^2 -1 =\sqrt{m^2+1} $
$m^4-2m^2+1=m^2+1$
$m^4=3m^2$
$m < 0 \ \ だから \quad m=-\sqrt{3}$
$増減表$
\[ \begin{array}{c||c|c|c|c|c} m& \cdots & -\sqrt{3} & \cdots & 0\\ \hline f'(m)& + & 0 & - & \\ \hline f(m)& \nearrow & 極大 & \searrow & \\ \end{array} \]
$m=-\sqrt{3}\ で \ f(m)\ は極大かつ最大となる。$
$\triangle OAB が最小となるのは、f(m) が最大のときで、このとき、 A(\sqrt{3},\ 0), \ \ B(0,\ 3)$
$(以下上の解答に同じ)$
メインメニュー に戻る