円の接線


$1\ \ はじめに$

$\hspace{1em} 円Oの接線をl,接点をAとすると　 OA \perp l$

$　これはなにかとよく使われる定理ですが、$
$その証明はとなると、中学校はもちろん$
$高校の教科書や参考書にも載っていません。$
$「図をみればわかるでしょ」的なノリでは$
$済まされない基本的で重要な内容を含んで$
$いるのです。$
$　そこで、この定理を掘り下げてみたいと$
$思います。$


$2\ \ 円と直線の位置関係$

$　円と直線の位置関係は、下図のように3通りあります。$

$\hspace{5em}$ 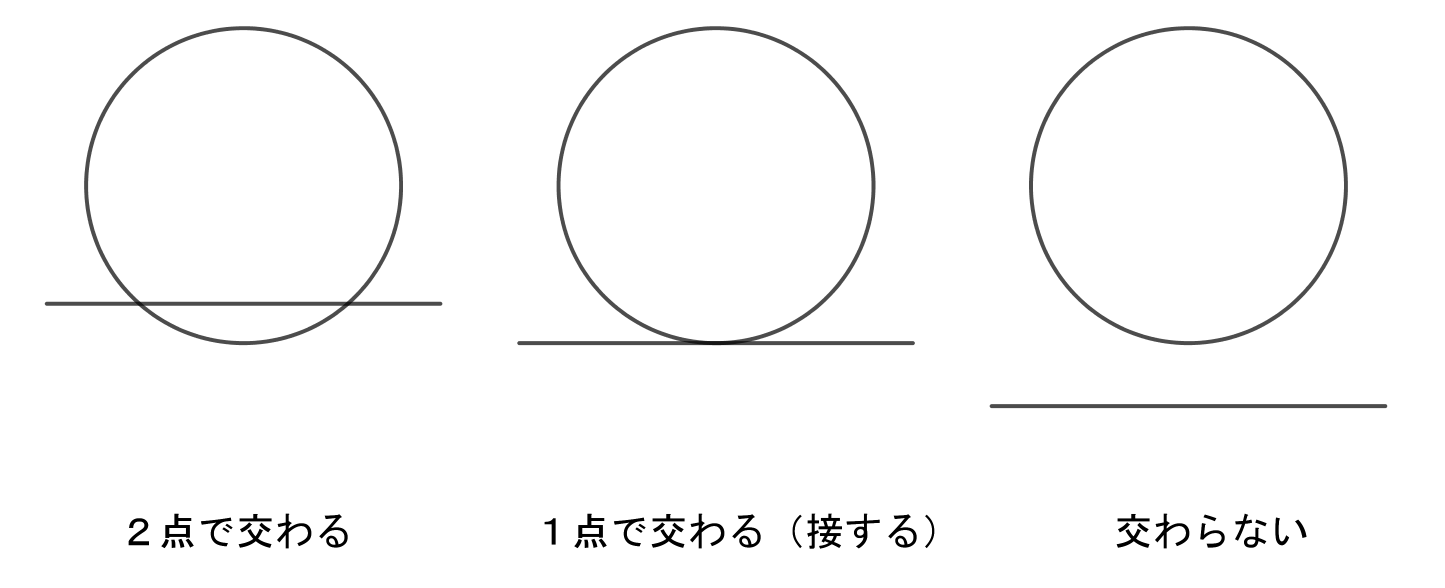$　特に、1点で交わるとき、直線は円に接するといい、この直線を接線、交わる1点を接点といいます。$




$3\ \ これで、準備が整いましたので、はじめの定理が証明できるようになりました。$

$定理　直線 \ l\ は点Aで円Oに接する　 \Longleftrightarrow \quad OA \perp l$


$\Longrightarrow の証明$

$背理法で証明する。$
$OA \perp l でないとすると、Oからlに垂線が1本$
$引けるから、その足をHとする。$
$l上にAH=BHとなるAと異なる点Bをとると$
$2辺とその間の角が等しいので$
$ \hspace{2em} △OHA \equiv △OHB$
$よって　 OA=OB$
$点Aは円周上の点だから、点Bも円周上の点である。$
$すると$
$lは円Oと異なる2点で交わることになり、lが接線であることに矛盾する。$
$したがって　OA \perp l$


$\Longleftarrow の証明$

$直線l上にA以外の点Bをとると$
$点と直線の最短距離は垂線であるら$
$\quad (このことについては($点と直線の距離$)を参考にしてください。)$

$\hspace{2em} OA < OB $
$よって、点Bは円Oの外部の点となる。$
$l \ は点A以外に円Oと共有点をもたないので$
$定義から \ l\ は円Oの接線である。$


$4\ \ 再び円と直線の位置関係$

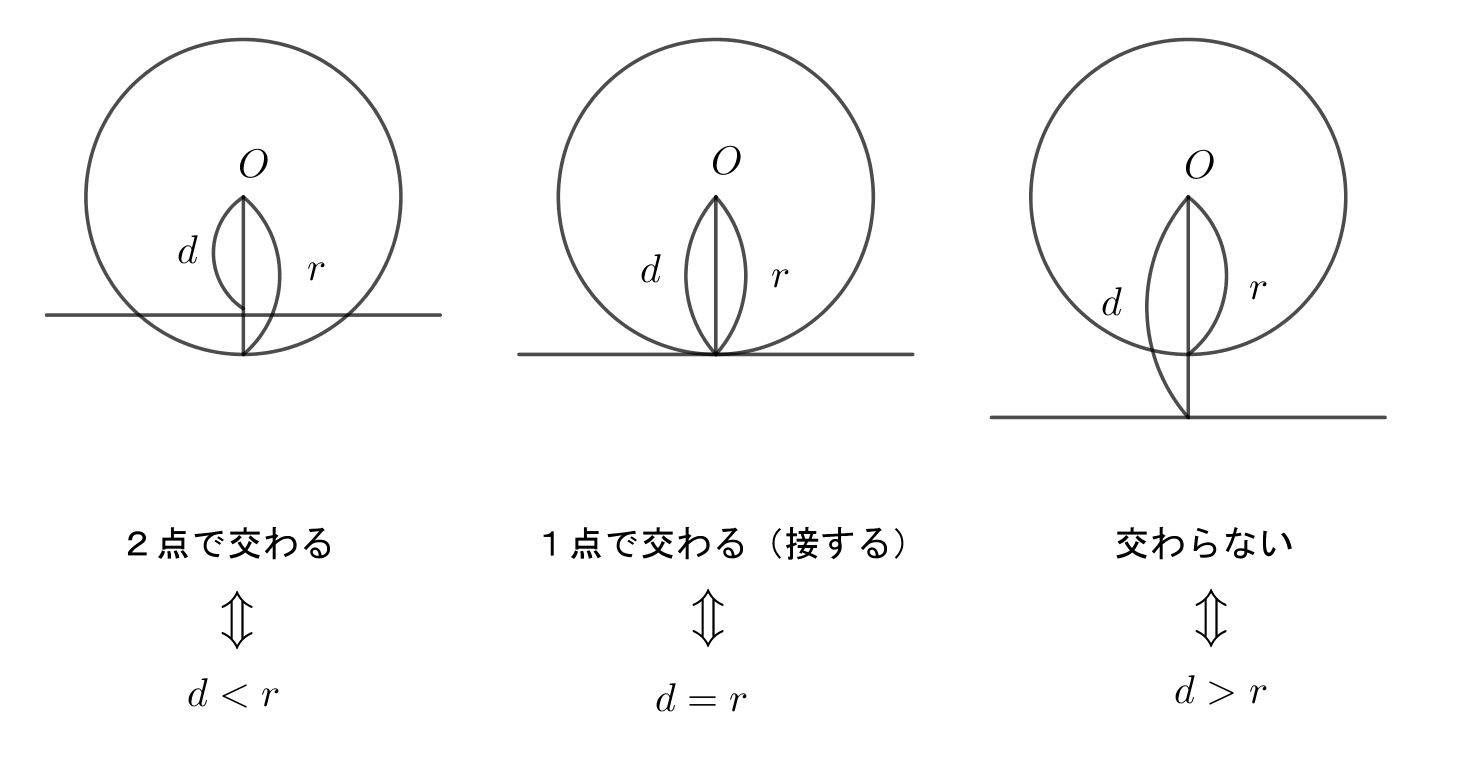
$円と直線の位置関係は、円の中心Oから直線lまでの距離dと、円の半径rを用いて表すと、$
$下図のようになります。$

$\hspace{5em}$

$5\ \ 円の接線の方程式$

$応用問題になりますが、４と５を使うと円周上の接点の座標が与えられた場合の接線lの方程式を$
$求めることができます。$

$座標平面で、円の中心をC(x_0,y_0),半径を$
$ \ r \ ,円周上の点を A(x_1,y_1) とすると$
$r=CA=\sqrt{(x_1-x_0)^2+(y_1-y_0)^2}$
$ACの傾き=\cfrac{y_1-y_0}{x_1-x_0}$
$l \perp AC だから$
$lの傾き=-\cfrac{x_1-x_0}{y_1-y_0}$
$よって l の方程式は$
$y=-\cfrac{x_1-x_0}{y_1-y_0}(x-x_1)+y_1$
$y_1を移項して、分母を払うと$
$(x_1-x_0)(x-x_1)+(y_1-y_0)(y-y_1)=0$
$(x_1-x_0)(x-x_0-(x_1-x_0))+(y_1-y_0)(y-y_0-(y_1-y_0))=0$
$(x_1-x_0)(x-x_0)+(y_1-y_0)(y-y_0)=(x_1-x_0)^2+(y_1-y_0)^2$
$右辺は線分\quad CA^2=r^2　だから$

$\hspace{2em} (x_1-x_0)(x-x_0)+(y_1-y_0)(y-y_0)=r^2$

$これが求める接線の方程式です。$



ページの先頭へ↑




メインメニュー　に戻る