早稲田大学(理系) 2022年 問題4
$一辺の長さが \ \sqrt{3}+1\ である正八面体の頂点を下図のように \ P_1,\ P_2,\ P_3,\ P_4,\ P_5,\ P_6\ とする。$
$各 \ i=1,\ 2,\ \cdots ,\ 6\ に対して、P_i\ 以外の \ 5\ 点を頂点とする四角錐(すい)のすべての面に内接する球(内部を含む)$
$を \ B_i\ とする。B_1\ の体積を \ X\ とし、B_1\ と \ B_2\ の共通部分の体積を \ Y\ とし、B_1,\ B_2,\ B_3\ の共通部分の体積を \ Z\ とする。$
$さらに \ B_1,\ B_2,\ \cdots,\ B_n\ を合わせて得られる立体の体積を \ V_n\ (n=2,\ 3,\ \cdots,\ 6)\ とする。以下の問に答えよ。$

$(1)\ \ V_n=aX+bY+cZ\ \ となる整数 \ a,\ b,\ c\ を \ n=2,\ 3,\ 6\ の場合について求めよ。$
$(2)\ \ X\ の値を求めよ。$
$(3)\ \ V_2\ の値を求めよ。$
$(解説)$
$(1)\ \ n=2,\ n=3\ までは簡単な図をかけばわかりますが、n=6\ はよほど正確な図を$
$\quad かかないとわかりづらいです。与えられた式からわかるように、4\ つの球が重なる$
$\quad ことはありません。$
$(2)\ \ 球が正方形と正三角形に接することから半径を求めます。$
$(3)\ \ 2球の中心間距離を求め、回転体の体積を求める方法で Y\ を求めます。$
(1)
(i)$\ \ n=2 \ \ の場合$


$\qquad V_2=2X-Y \quad より \quad a=2,\ \ b=-1,\ \ c=0$
(ii)$\ \ n=3 \ \ の場合$


$\qquad V_3=3X-3Y+Z \quad より \quad a=3,\ \ b=-3,\ \ c=1$
(iii)$\ \ n=6 \ \ の場合$
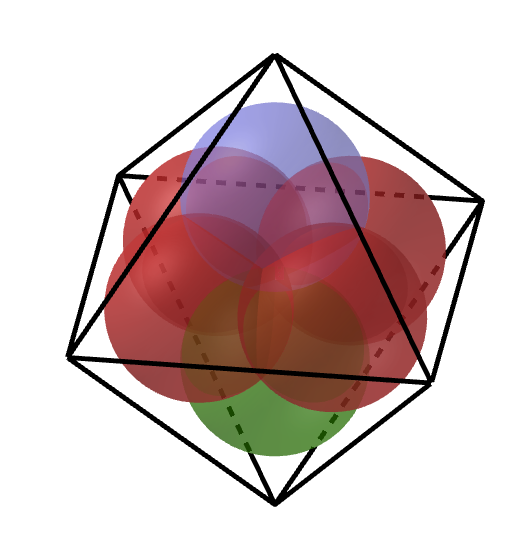

$\quad B_1\ と\ B_6,\ B_2\ と \ B_5,\ B_3\ と \ B_4\ は互いに接する。$
$\quad 2\ つの球が重なっている部分が 赤球と赤球で \ 4\ つ、赤球と青球で \ 4\ つ、赤球と緑球で \ 4\ つで合計 \ 12\ 個$
$\quad 3\ つの球が重なっている部分が 赤球と赤球と青球で \ 4\ つ、赤球と赤球と緑球で \ 4\ つで合計 \ 8\ 個$
$\qquad V_6=6X-12Y+8Z \quad より \quad a=6,\ \ b=-12,\ \ c=8$
(2)

$正八面体の一辺の長さ\ \sqrt{3}+1\ を \ a ,\ \ 球B_1\ の半径を \ r\ とおく。$
$右図で正方形 \ P_2P_3P_5P_4\ と球 \ B_1\ の接点を \ O、球 \ B_1\ の中心を \ C、$
$辺 \ P_2P_3 \ の中点を \ A、線分 \ P_6A\ に中心 \ C\ から下ろした垂線との$
$交点を \ B\ とする。$
$\triangle P_6P_2P_3 \ は正三角形だから \quad P_6A \perp P_2P_3 \quad \therefore \ \ P_6A=P_6P_2\sin 60°=\cfrac{\sqrt{3}}{2}a$
$二等辺三角形 \ P_6P_2P_5\ \ において点 \ O\ は辺 \ P_2P_5\ の中点だから \quad P_6O \perp P_2P_5$
$同様に、二等辺三角形 \ P_6P_3P_4\ \ において点 \ O\ は辺 \ P_3P_4\ の中点だから \quad P_6O \perp P_3P_4$
$よって、P_6O\ は交わる \ 2\ 直線 \ P_2P_5,\ P_3P_4\ にそれぞれ直交するから \quad P_6O \perp 正方形 \ P_2P_3P_5P_4$
$\qquad (このことについては($三垂線の定理$)を参考にしてください。)$
$また、球 \ B_1\ は点 \ O\ で正方形 \ P_2P_3P_5P_4\ に接するから \quad CO \perp 正方形 \ P_2P_3P_5P_4$
$したがって、3\ 点 \ P_6,\ C,\ O\ は一直線上にある。$
$P_6O \perp 正方形 \ P_2P_3P_5P_4 \quad より \quad P_6O \perp OA$
$よって \quad P_6O=\sqrt{P_6A^2-OA^2}=\sqrt{\cfrac{3}{4}a^2-\cfrac{1}{4}a^2}=\cfrac{a}{\sqrt{2}}$
$\quad P_6C=P_6O-r=\cfrac{a}{\sqrt{2}}-r$
$一方$
$r=CB=P_6C \sin \angle CP_6B=P_6C \times \cfrac{OA}{P_6A}=(\cfrac{a}{\sqrt{2}}-r) \times \cfrac{ \dfrac{a}{2}} {\dfrac{ \sqrt{3}a}{ {2} } }
=(\cfrac{a}{\sqrt{2}}-r) \times \cfrac{1}{\sqrt{3}}$
$\sqrt{3}r=\cfrac{a}{\sqrt{2}}-r \qquad (\sqrt{3}+1)r=\cfrac{a}{\sqrt{2}} \qquad \therefore \ \ r=\cfrac{a}{\sqrt{2}(\sqrt{3}+1)}$
$a=\sqrt{3}+1 \quad だから \quad r=\cfrac{1}{\sqrt{2}}$
$よって \quad X=\cfrac{4}{3}\pi r^3=\cfrac{4}{3}\pi \times \cfrac{1}{2\sqrt{2}}=\cfrac{\sqrt{2}}{3}\pi$
(3)

$B_1,\ B_2\ の中心をそれぞれ \ C_1,\ C_2\ とすると$
$球 \ B_1\ は正方形 \ P_2P_3P_5P_4\ の中心 \ O\ で接するから \qquad C_1O \perp 正方形P_2P_3P_5P_4 $
$C_2O\ は正方形 \ P_2P_3P_5P_4\ 上の直線だから \qquad C_1O \perp C_2O $
$2\ つの球の半径はともに \ r\ であるから三角形 \ OC_1C_2\ は直角二等辺三角形となり$
$\quad C_1C_2=\sqrt{2}C_1O=\sqrt{2}r$

$Y\ の値は回転体の体積を求める方法をつかって$
\[\quad Y=2\pi \int _{\scriptsize{\cfrac{r}{\sqrt{2}}}}^r (r^2-x^2)dx=2\pi\big[r^2x-\cfrac{x^3}{3}\big]_{\scriptsize{\cfrac{r}{\sqrt{2}}}}^r
=\cfrac{8-5\sqrt{2}}{6}\pi r^3\]
$(2)より \quad r=\cfrac{1}{\sqrt{2}} \quad だから \quad Y=\cfrac{8-5\sqrt{2}}{6}\pi \times \cfrac{1}{2\sqrt{2}}=\cfrac{4\sqrt{2}-5}{12}\pi$
$よって \quad V_2=2X-Y=2 \times \cfrac{\sqrt{2}}{3}\pi - \cfrac{4\sqrt{2}-5}{12}\pi=\cfrac{5+4\sqrt{2}}{12}\pi$
メインメニュー に戻る