2変数関数の極大・極小
(1) 極大・極小の定義
$2変数関数f(x,y)が点(a,b)の近傍Uで定義されていて、任意の\ \delta > 0\ に対して$
$\qquad |x-a| < \delta ,\quad |y-b| < \delta であるすべてのx,\ yに対して\quad f(x,y) \leqq f(a,b)$
$であるとき、f(a,b) を広義の極大値という。$
$とくに、(x,y) \neq (a,b) \ で\ f(x,y) < f(a,b) \ であるとき、f(a,b) を狭義の極大値という。$
$不等号を逆にした場合を極小値といい、極大値と極小値をあわせて極値という。$
$f(x,y)が(a,b)において極値をもてば$
$\quad 1変数関数f(x,b)は明らかに極値をもつから \quad f_x(a,b)=0$
$\quad 1変数関数f(a,y)も明らかに極値をもつから \quad f_y(a,b)=0$
$である。この(a,b)をf(x,y)の停留点という。$
(2) 極大・極小の判定
$\qquad f(x,y)は点(a,b)の近傍でC^2級、点(a,b)は停留点とする。$
$\hspace{3em} A=f_{xx}(a,b), \ B=f_{xy}(a,b) , \ C=f_{yy}(a,b) , \ \Delta =B^2-AC \ \ とおくと$
$\hspace{3em}$(i)$\ \Delta < 0 ,\quad A > 0 \ ならば (a,b) \ は狭義の極小点$
$\hspace{3em}$(ii)$\ \Delta < 0 ,\quad A < 0 \ ならば (a,b) \ は狭義の極大点$
$\hspace{3em}$(iii)$\ \Delta > 0 \ ならば (a,b) \ は極大点でも極小点でもない。$
$\hspace{3em}$(iv)$\ \Delta =0 \ ならばこれだけでは判定できない。$
$(証明)$
$(h,k)は(0,0)に十分近いとする。ただしk \neq 0$
$f(x,y)\ は\ 点(a,b)が停留点だから f_x(a,b)=0,\quad f_y(a,b)=0$
$1変数関数 \ g(t)=f(a+ht,b+kt) を考えると$
$\quad g'(0)=hf_x(a,b)+kf_y(a,b)=0$
$\quad g''(0)=h^2f_{xx}(a,b)+2hkf_{xy}(a,b)+k^2f_{yy}(a,b)$
$\hspace{4em} =k^2\{(\cfrac{h}{k})^2f_{xx}(a,b)+2(\cfrac{h}{k})f_{xy}(a,b)+f_{yy}(a,b)\}$
$\quad \cfrac{h}{k}=u \ とおくと$
$\quad g''(0)=k^2(Au^2+2Bu+C)$
$uについての2次式の判別式が\Delta だから$
$\qquad \Delta \ < 0 \ ならば \ g''(0)\ はAと同符号となり$
$\qquad $ (i)$A > 0 \ ならば \ g''(0)>0 \ となり、\ g(t)\ は \ t=0 \ で極小$
$\qquad $ (ii)$A < 0 \ ならば \ g''(0)<0 \ となり、\ g(t)\ は \ t=0 \ で極大$
$\qquad \Delta> \ 0 \ ならば \ g''(0)\ は正、負の値をもつから (a,b)は極大でも極小でもない。$
$これで証明できたように思えますが、実は不十分です。$
$g(t)はx方向とy方向のみの変化しか考えていないからです。$
$2変数関数はあらゆる方向について考えなくてはならないのです。$
$そこで、次のように修正します。$
$f(x,y)\ を点(a,b)のまわりにテーラー展開すると$
$\quad f(a+h,b+k)-f(a,b)=hf_x(a,b)+kf_y(a,b)+\cfrac{1}{2}\{h^2f_{xx}(\xi,\eta)+2hkf_{xy}(\xi,\eta)+k^2f_{yy}(\xi,\eta)\}$
$ただし \quad \xi=a+\theta h,\quad \eta=b+\theta k \quad (0 < \theta <1)と表せます。$
$\quad \varepsilon_1=f_{xx}(\xi,\eta)-f_{xx}(a,b)=f_{xx}(\xi,\eta)-A$
$\quad \varepsilon_2=f_{xy}(\xi,\eta)-f_{xy}(a,b)=f_{xy}(\xi,\eta)-B$
$\quad \varepsilon_3=f_{yy}(\xi,\eta)-f_{yy}(a,b)=f_{yy}(\xi,\eta)-C$
$とおくと、f(x,y)は \ C^2 \ 級だからf_{xx},\ f_{xy},\ f_{yy}はすべて連続である。$
$したがって \qquad (h,k) \rightarrow (0,0)\ のとき\ \ \varepsilon_1 \rightarrow 0, \ \varepsilon_2 \rightarrow 0, \ \varepsilon_3 \rightarrow 0$
$ここで、すべての方向の極限を考える工夫が必要です。$
$h=r\cos \theta,\ k=r\sin \theta \quad (r > 0)とおくことです。$
$\hspace{3em}f(a+h,b+k)-f(a,b)$
\begin{eqnarray*} &=&hf_x(a,b)+kf_y(a,b)+\cfrac{1}{2}\{h^2f_{xx}(\xi,\eta)+2hkf_{xy}(\xi,\eta)+k^2f_{yy}(\xi,\eta)\}\\ &=&\cfrac{r^2}{2}\{(A+\varepsilon_1)\cos ^2\theta +2(B+\varepsilon_2)\cos \theta \sin \theta +(C+\varepsilon_3)\sin ^2\theta\}\\ &=&\cfrac{r^2}{2}(A\cos ^2\theta +2B\cos \theta \sin \theta +C\sin ^2\theta +\varepsilon_1\cos ^2\theta +2\varepsilon_2\cos \theta \sin \theta +\varepsilon_3\sin^2\theta )\\ \end{eqnarray*} $ここで D=\varepsilon_1\cos ^2\theta+2\varepsilon_2\cos \theta \sin \theta +\varepsilon_3\sin^2\theta は$
$\quad |D| \leqq |\varepsilon_1\cos ^2\theta|+2|\varepsilon_2 \cos \theta \sin \theta|+|\varepsilon_3\sin^2\theta | \leqq \varepsilon_1 + 2\varepsilon_2 + \varepsilon_3 だから$
$\quad r \rightarrow 0 のとき (h,k) \rightarrow 0 となり D \rightarrow 0$
$したがって 十分小さな\ r\ に対して$
$f(a+h,b+k)-f(a,b)$
\begin{eqnarray*} &=&\cfrac{r^2}{2}(A\cos ^2\theta +2B\cos \theta \sin \theta +C\sin ^2\theta )\\ &=&\cfrac{r^2}{2}A\big(\cos ^2 \theta +2\cfrac{B}{A}\cos \theta \sin \theta +\cfrac{C}{A}\sin ^2\theta \big)\\ &=&\cfrac{r^2}{2}A\big\{\big(\cos \theta +\cfrac{B}{A}\sin \theta \big)^2-\cfrac{B^2-AC}{A^2}\sin ^2\theta \big\}\\ \end{eqnarray*} $よって \Delta=B^2-AC<0 で$
$\quad$ (i)$\ A>0 \ ならば f(a+h,b+k)-f(a,b) > 0 \ となり f(a,b) \ は極小値$
$\quad$ (ii)$\ A<0 \ ならば f(a+h,b+k)-f(a,b) < 0 \ となり f(a,b) \ は極大値$
$\Delta=B^2-AC >0 \ ならば$
$\qquad f(a+h,b+k)-f(a,b) \ は正にも負にもなるから極大でも極小でもない$
$これで、2変数関数が極値となる条件がわかりました。$
例題
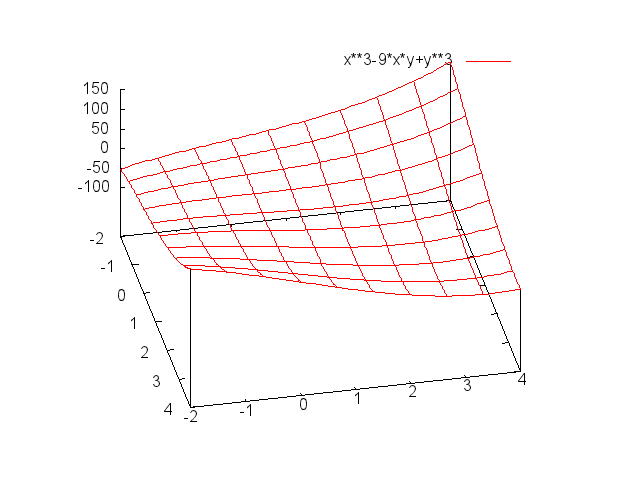
$f(x,y)=x^3-9xy+y^3 の極値を調べてみましょう。$
$\quad f_x(x,y)=3x^2-9y=0 \hspace{10em}(1)$
$\quad f_y(x,y)=-9x+3y^2=0 \hspace{9em}(2)$
$(1)より y = \cfrac{1}{3}x^2 \hspace{13em} (3)$
$(2)に代入して$
$\quad -3x+\big(\cfrac{1}{3}x^2\big)^2=0$
$\quad x^4-27x=0$
$\quad x(x^3-27)=0$
$\quad \therefore x=0,\ 3$
$それぞれ(3)に代入して \quad y=0,\ 3$
$よって 停留点は O(0,\ 0),\ \ P(3, \ 3)$
$f_{xx}(x,y)=6x,\ f_{xy}(x,y)=-9,\ f_{yy}(x,y)=6y に代入して$
(i)$\ 点O(0,0)\ \ は$
$\qquad A=0,\ B=-9,\ C=0 だから \Delta=81 \ で極大でも極小でもない(鞍点といいます)$
(ii)$\ 点P(3,\ 3)\ \ は$
$\qquad A=18,\ B=-9,\ C=18 だから \Delta=(-9)^2-18 \times 18=-243 \ で極小$
$\qquad 極小値は f(3,3)=3^3-9 \times 3 \times 3 +3^3=-27$
$h(x,\ y)のグラフは下図のとおりです。$
$見にくいのですが、(3,\ 3) で極小となっているのがなんとなくわかります。$
メインメニュー に戻る