東北大学（理系）2018年前期　問題６

$　xy平面内の図形$
\[ S: \left\{ \begin{array}{ll} x+y^2 \leqq 2 \\ x+y \geqq 0 \\ x-y \leqq 2 \end{array} \right. \] $を考える。図形Sを直線y=-xのまわりに1回転して得られる立体の体積をVとする。$
$(1)\ \ Sをxy平面に図示せよ。$
$(2)\ \ Vを求めよ。$


$いわゆる斜回転の回転体の体積を求める問題です。$
$詳しくは $ 斜回転による回転体の体積$を参考にしてください。$


(1)

　

$領域Sは右図のとおり$
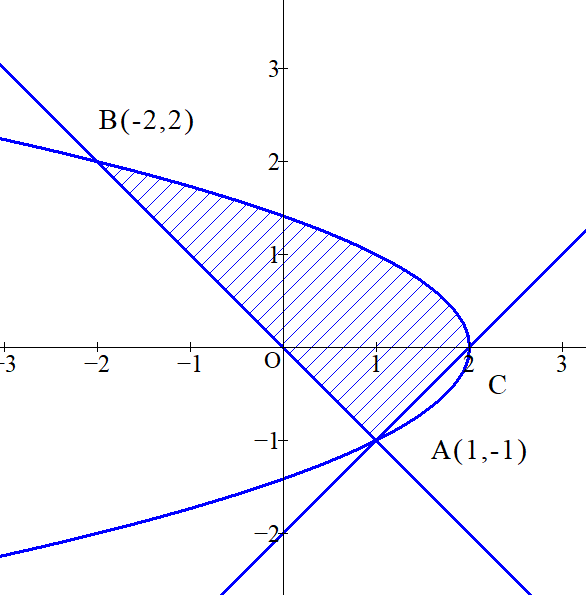
$境界を含みます$


(2)

$x+y^2 =2 　と　x+y = 0 　の交点は$
$x=-y 　を代入して　-y+y^2=2 　より$
$y=-1,2 　順に　x=1,-2$
$したがって交点は　　A(1,-1),\ B(-2,2)$


$解１　 回転軸に垂直な直線で分割する方法 $

　

$直線 \ y=-x \ の単位方向ベクトルは、yが増加する向きを$
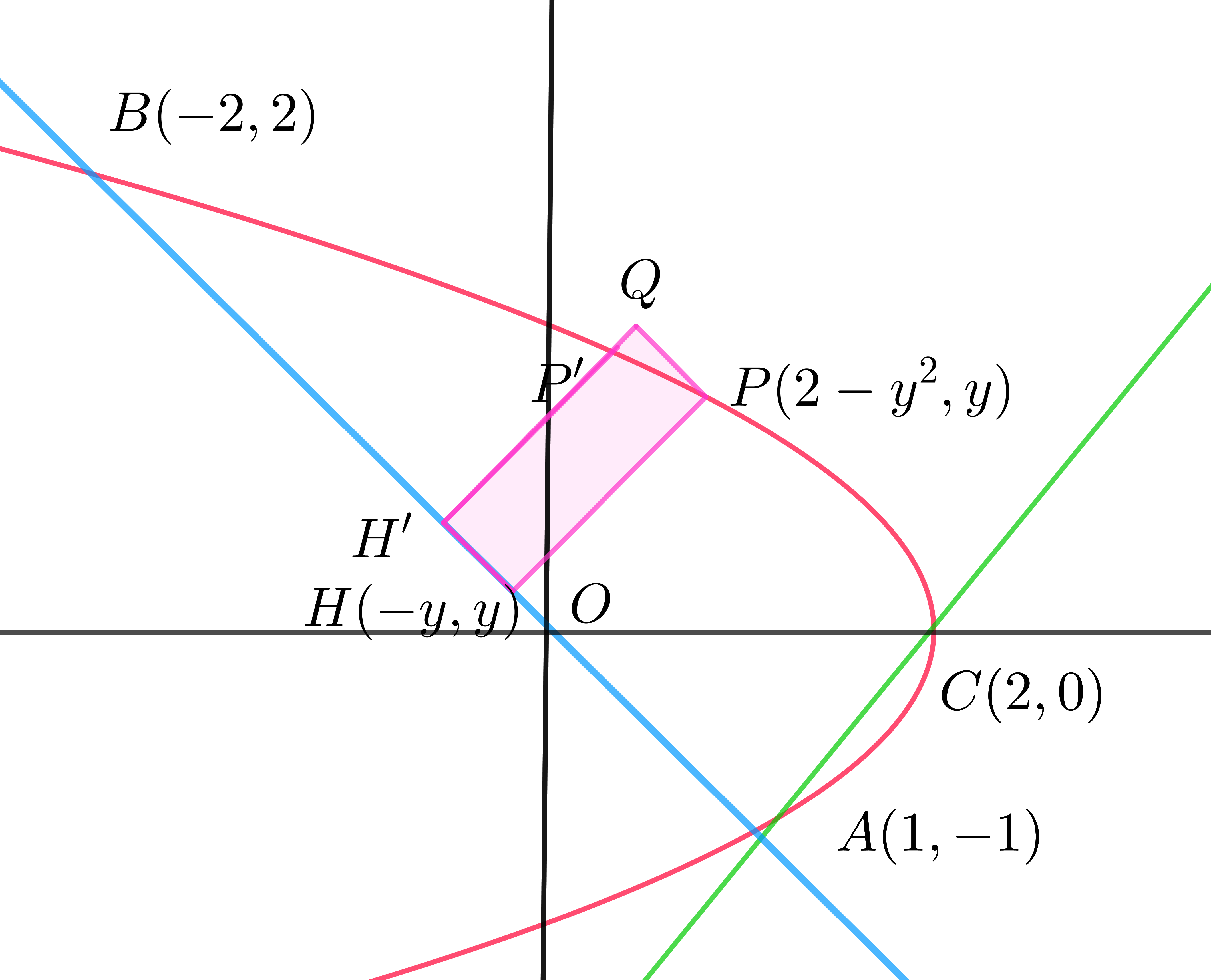
$正として$
$\quad \vec {u}=\big(-\cfrac{1}{\sqrt{2}},\cfrac{1}{\sqrt{2}}\big)$

$f(y)=2-y^2 　とおく。$

$dy を微小量として　P(f(y),y),\ P'(f(y+dy),y+dy) \ とすると$

$\quad f(y+dy)=f(y)+f'(y)dy 　だから$
$\quad \vec{PP'}=\big(f(y)+f'(y)dy,\ y+dy \big)-\big(f(y),\ y\big)=\big(f'(y)dy,\ dy\big)$

$2点P,P'から　l:y=-x \ に下ろした垂線の足をそれぞれ H,H' とすると$
\begin{eqnarray*} |\vec{HH'}|&=&\vec{u} \cdot \vec{PP'}\\ &=&\big(-\cfrac{1}{\sqrt{2}},\cfrac{1}{\sqrt{2}}\big) \cdot \big(f'(y)dy,\ dy\big)\\ &=&\cfrac{1-f'(y)}{\sqrt{2}}dy\\ &=&\cfrac{1+2y}{\sqrt{2}}dy\\ \end{eqnarray*} $また$
$\quad PH=\cfrac{f(y)+y}{\sqrt{2}}=\cfrac{2-y^2+y}{\sqrt{2}}$

$PQ // HH' ,PQ=HH' \ となるように点Ｑをとると、四角形PQH'H は長方形となる。$
$この小長方形を\ l\ のまわりに回転してできる円柱の体積は$
\begin{eqnarray*} dV&=&\pi PH^2\ HH'\\ &=&\cfrac{\pi}{2\sqrt{2}}(2-y^2+y)^2(1+2y)dy\\ &=&\cfrac{\pi}{2\sqrt{2}}(2y^5-3y^4-8y^3+5y^2+12y+4)dy\\ \end{eqnarray*} $したがって、点Pのy座標がとる範囲が　0 \leqq y \leqq 2 \ \ であることから$
\begin{eqnarray*} V&=&\int _0 ^2 dV\\ &=&\cfrac{\pi}{2\sqrt{2}}\int _0 ^2 (2y^5-3y^4-8y^3+5y^2+12y+4)dy\\ \\ &=&\cfrac{58\sqrt{2}}{15}\pi\\ \end{eqnarray*}

$この解法はわかりやすい反面、被積分項の次数が上がる欠点があります。$


$解 2 　傘型積分で求める方法 $

　

$放物線上の任意の点P(f(y),y)から直線 \ y=-x \ に下ろした$
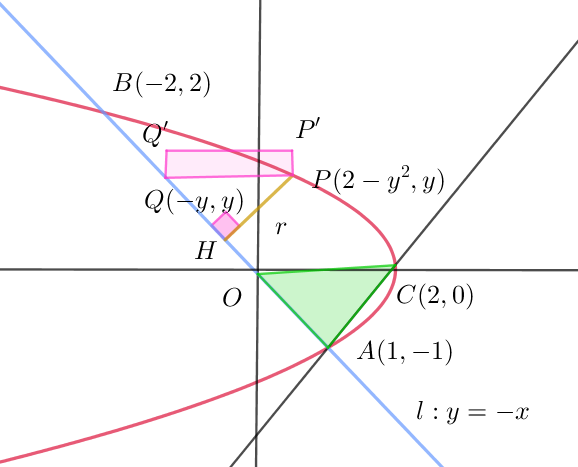
$垂線の足をHとすると$
$\quad r=PH=PQ\cos 45°=\cfrac{PQ}{\sqrt{2}}$

$点Pを通るx軸に平行な直線と\ y=-x\ との交点を$
$Q(-y,y)\ とする。$
$さらに2点、P'(f(y),y+dy),Q'(-y,y+dy)をとり,$
$長方形PP'Q'Q　をつくる。$

$この長方形PP'Q'Q\ をy=-x \ のまわりに一回転してできる回転体は円錐だから$
$(ここも$ 斜回転による回転体の体積$を参考にしてください。)$
$その表面積は$
\begin{eqnarray*} S&=&\pi PQ\cdot r\\ &=&\cfrac{\pi}{\sqrt{2}}PQ^2\\ &=&\cfrac{\pi}{\sqrt{2}}(2-y^2+y)^2\\ &=&\cfrac{\pi}{\sqrt{2}}(y+1)^2(y-2)^2\\ \end{eqnarray*}
$円錐の厚さがdy であるから$
$\qquad \therefore dV=\cfrac{\pi}{\sqrt{2}}(y+1)^2(y-2)^2dy$

$したがって 放物線と直線とx軸で囲まれた領域の回転体の体積は、yのとる範囲に注意して$
\begin{eqnarray*} V_1&=&\int _0 ^2 Sdy\\ &=&\cfrac{\pi}{\sqrt{2}}\int _0 ^2 (y+1)^2 (y-2)^2dy\\ &=&\cfrac{\pi}{\sqrt{2}}\big\{ \big [(y+1)^2 \cfrac{(y-2)^3}{3} \big ] _0 ^2 - \int _0 ^2 2(y+1)\cfrac{(y-2)^3}{3}dy \big\}\\ &=&\cfrac{\pi}{\sqrt{2}}\big\{ \cfrac{8}{3} - \cfrac{2}{3}\int _0 ^2 (y+1)(y-2)^3dy \big\}\\ &=&\cfrac{\pi}{\sqrt{2}}\big\{\cfrac{8}{3} - \cfrac{2}{3}\big\{\big[(y+1) \cfrac{(y-2)^4}{4}\big] _0 ^2 - \int _0 ^2 \cfrac{(y-2)^4}{4}dy \big\}\big\}\\ &=&\cfrac{\pi}{\sqrt{2}}\big\{\cfrac{8}{3} + \cfrac{8}{3}+ \cfrac{1}{6} \int _0 ^2 (y-2)^4dy\big\}\\ &=&\cfrac{\pi}{\sqrt{2}}\big\{\cfrac{16}{3} + \cfrac{1}{6} \big[\cfrac{(y-2)^5}{5}\big ] _0 ^2\big\}\\ &=&\cfrac{16\sqrt{2}}{5}\pi\\ \end{eqnarray*}
$右図の緑色の三角形の回転体は$
$底面は半径 \ \sqrt{2}の円、高さは \ \sqrt{2}の円錐だから体積は$
$\quad V_2=\cfrac{1}{3}\times \pi \times 2 \times \sqrt{2}=\cfrac{2\sqrt{2}}{3}\pi$

$よって求める体積は$
\begin{eqnarray*} V&=&V_1 + V_2\\ &=&\cfrac{16\sqrt{2}}{5}\pi + \cfrac{2\sqrt{2}}{3}\pi\\ &=&\cfrac{58\sqrt{2}}{15}\pi \\ \end{eqnarray*}

$なお、上の定積分の計算で部分積分法を用いましたが、他に被積分関数$
$\quad I(y)=(y+1)^2 (y-2)^2　を$

$(1)\ \ そのまま展開する方法$

$\qquad I(y)=y^4-2y^3-3y^2+4y+4$

$(2)\ \ (y-2) で展開する方法$
\begin{eqnarray*} I(y)&=&(y-2+3)^2(y-2)^2\\ &=&\{(y-2)^2+6(y-2)+9\}(y-2)^2\\ &=&(y-2)^4+6(y-2)^3+9(y-2)^2\\ \end{eqnarray*}
$があります。$




ページの先頭へ↑



メインメニュー　に戻る