東北大学(理系)2018年前期 問題4
$ 三角形ABCの内接円の半径を\ r\ ,外接円の半径を\ R\ とし、h=\cfrac{r}{R} \ とする。$
$また、∠A=2\alpha,\ ∠B=2\beta,\ ∠C=2\gamma \ とおく。$
$(1) \quad h=4\sin \alpha \sin\beta \sin\gamma \ となることを示せ。$
$(2) \quad 三角形ABCが直角三角形のとき \ h\leqq \sqrt{2}-1 \ が成り立つことを示せ。$
$\qquad また、等号が成り立つのはどのような場合か。$
$(3) \quad 一般の三角形ABCに対して \ h \leqq \cfrac{1}{2} \ が成り立つことを示せ。$
$\qquad また、等号が成り立つのはどのような場合か。$
$(1)は正弦定理と余弦定理を用いて、あとの変形には和積の公式をつかいます。$
$(2)は加法定理と合成の公式で求まります。$
$(3)は2変数の最大値を求める問題ですので、本来は高校のレベルを超えますが、$
$\quad 入試ではときどき見かけます。一方の変数を定数として扱います。$
$\quad 別解として、大学1年程度の解析学で学ぶ2変数関数の最大・最小問題を考えましょう。$
(1)

$\qquad \cfrac{a}{\sin A}=\cfrac{b}{\sin B}=\cfrac{c}{\sin C}=2R$
$\qquad \therefore a=2R\sin A,\ \ b=2R\sin B,\ \ c=2R\sin C$
$よって$
\begin{eqnarray*} △ABC&=&\cfrac{1}{2}bc\sin A\\ &=&\cfrac{1}2 \times 2R\sin B \times 2R\sin C \times \sin A\\ &=&2R^2\sin A\sin B\sin C\\ &=&2R^2\sin 2 \alpha \sin 2\beta \sin 2\gamma\\ &=&16R^2\sin \alpha \sin \beta \sin \gamma \cos \alpha \cos \beta \cos \gamma\\ \end{eqnarray*}
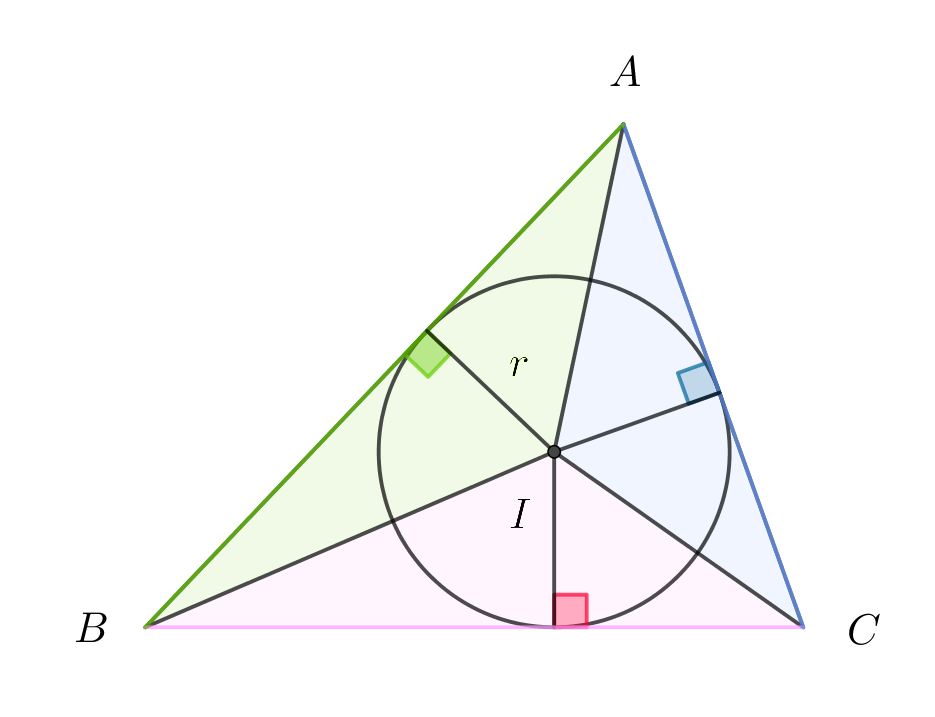
\begin{eqnarray*} △ABC&=&△ABI+△BCI+△CAI\\ &=&\cfrac{r}{2}(a+b+c)\\ &=&\cfrac{r}{2}(2R\sin A+2R\sin B+ 2R\sin C)\\ &=&R\ r(\sin A+\sin B+\sin C)\\ &=&R\ r\big(2\sin \cfrac{A+B}{2}\cos \cfrac{A-B}{2} + \sin C \big)\\ &=&R\ r\big(2\sin \cfrac{\pi -C}{2}\cos \cfrac{A-B}{2} + \sin C \big)\\ &=&R\ r\big(2\cos \cfrac{C}{2}\cos \cfrac{A-B}{2} + 2\sin \cfrac{C}{2}\cos \cfrac{C}{2} \big)\\ &=&2R\ r\cos \cfrac{C}{2}\big(\cos \cfrac{A-B}{2} + \sin \cfrac{C}{2} \big)\\ &=&2R\ r\cos \cfrac{C}{2}\big(\cos \cfrac{A-B}{2} + \sin \cfrac{\pi-A-B}{2} \big)\\ &=&2R\ r\cos \cfrac{C}{2}\big(\cos \cfrac{A-B}{2} + \cos \cfrac{A+B}{2} \big)\\ &=&2R\ r\cos \cfrac{C}{2} \times 2\cos \cfrac{A}{2}\cos \cfrac{B}{2}\\ &=&4R\ r\cos \alpha \cos \beta \cos \gamma \\ \end{eqnarray*} $よって$
$\qquad 16R^2\sin \alpha \sin \beta \sin \gamma \cos \alpha \cos \beta \cos \gamma = 4R\ r\ cos \alpha \cos \beta \cos \gamma $
$\qquad 4R\sin \alpha \sin \beta \sin \gamma = r$
$\qquad h=\cfrac{r}{R}=4\sin \alpha \sin \beta \sin \gamma $
$実は、この A+B+C=\pi のとき \quad \sin A +\sin B + \sin C =4\cos \cfrac{A}{2} \cos \cfrac{B}{2} \cos \cfrac{C}{2} $
$は、問題集に必ずのっている、和積の変換のスタンダードな問題です。$
(2)
$∠C=∠R としても一般性を失わない。$
$このとき \gamma =\cfrac{\pi}{4},\quad \alpha +\beta =\cfrac{\pi}{2}-\cfrac{\pi}{4}=\cfrac{\pi}{4}$
\begin{eqnarray*} h&=&4\sin \alpha \sin \beta \sin \cfrac{\pi}{4}\\ &=&2\sqrt{2}\sin \alpha \sin \beta\\ &=&2\sqrt{2}\sin \alpha \sin (\cfrac{\pi}{4}-\alpha)\\ &=&2\sqrt{2}\sin \alpha \big(\cfrac{1}{\sqrt{2}}\cos \alpha - \cfrac{1}{\sqrt{2}}\sin \alpha \big)\\ &=&2\sin \alpha \cos \alpha - 2\sin ^2\alpha\\ &=&\sin 2\alpha - (1-\cos 2\alpha)\\ &=&\sin 2\alpha +\cos 2\alpha -1\\ &=&\sqrt{2}\sin (2\alpha +\cfrac{\pi}{4})- 1\\ \end{eqnarray*} $\quad 0< 2\alpha < \cfrac{\pi}{2} だから \cfrac{\pi}{4} < 2\alpha+\cfrac{\pi}{4} < \cfrac{3}{4}\pi$
$よって$
$2\alpha+\cfrac{\pi}{4}=\cfrac{\pi}{2} すなわち \alpha =\cfrac{\pi}{8} \ のとき \sin (2\alpha +\cfrac{\pi}{4})=1 \ をとる$
$したがって \quad h \leqq \sqrt{2}-1$
$このとき \beta=\cfrac{\pi}{4} - \cfrac{\pi}{8}=\cfrac{\pi}{8} だから A=2\alpha=\cfrac{\pi}{4},\quad B=2\beta=\cfrac{\pi}{4} $
$よって、△ABCは直角二等辺三角形である$
(3)
$\alpha + \beta + \gamma=\cfrac{\pi}{2} より \gamma=\cfrac{\pi}{2}-\alpha -\beta$\begin{eqnarray*} h&=&4\sin \alpha \sin \beta \sin \gamma\\ &=&4\sin \alpha \sin \beta \sin (\cfrac{\pi}{2}-\alpha -\beta)\\ &=&4\sin \alpha \sin \beta \cos (\alpha +\beta )\\ \\ &=&2\sin \alpha \{\sin(\alpha +2\beta)-\sin \alpha \}\\ \end{eqnarray*} $hは\alpha,\ \beta \ の2変数関数であるから h=h(\alpha , \beta) とおく。$
$まず、\alpha \ を固定して考えると \ h\ は \ \sin(\alpha +2\beta)=1 のとき最大となる。$
$このとき \quad \alpha + 2\beta=\cfrac{\pi}{2} より \beta=\cfrac{\pi}{4}-\cfrac{\alpha}{2}$
$最大値は h^*(\alpha)=2\sin \alpha (1-\sin \alpha )$
$次に、この \ h^*(\alpha) \ の最大値を求める。$
$\sin \alpha =t とおくと 0 < \alpha < \cfrac{\pi}{2} だから 0 < t < 1$
$h^*(\alpha)=2t(1-t)=-2(t-\cfrac{1}{2})^2+\cfrac{1}{2}$
$t=\cfrac{1}{2} \ のとき最大値 \ \cfrac{1}{2} \ をもつ。$
$したがって h \leqq \cfrac{1}{2}$
$なお、\sin \alpha =\cfrac{1}{2} より \alpha=\cfrac{\pi}{6} このとき \beta=\cfrac{\pi}{6} , \quad \gamma=\cfrac{\pi}{6} となり$
$△ABCは A=B=C=60°\ の正三角形である。$
$おそらくこの解答で良いかと思います。$
$\alpha , \ \beta \ は2つの独立変数であるから、まず、\alpha を一定な値に固定して、\beta の関数ととらえ、$
$その最大値を \ \alpha \ の関数として、さらにその最大値を考えているわけです。$
$ところが、いつもこの方法でうまくいくとはかぎりません。$
$2変数関数には2変数関数なりの手を考える必要があるのです。$
$詳しくは $ 2変数関数の極大・極小$を参考にしてください。$
$次に、この手を使った、偏微分法を用いた別解を考えましょう。$
$h(\alpha , \beta )=4\sin \alpha \sin \beta \cos (\alpha +\beta )$
$h_\alpha (\alpha,\beta) =0 より$
$\quad 4\sin \beta\{\cos \alpha \cos (\alpha + \beta )-\sin \alpha \sin (\alpha + \beta )\}=0$
$\quad 4\sin \beta \cos (2\alpha +\beta )=0$
$\quad \sin \beta \neq 0 だから \cos (2\alpha +\beta )=0 より 2\alpha +\beta =\cfrac{\pi}{2} \hspace{5em}(1)$
$h_\beta (\alpha,\beta) =0 より$
$\quad 4\sin \alpha \{\cos \beta \cos (\alpha + \beta )-\sin \beta \sin (\alpha + \beta )=0$
$\quad 4\sin \alpha \cos (\alpha +2\beta )=0$
$\quad \sin \alpha \neq 0 だから \cos (\alpha +2\beta )=0 より \alpha +2\beta =\cfrac{\pi}{2} \hspace{5em}(2)$
$(1),(2) を解いて \alpha = \beta = \cfrac{\pi}{6}$
$\quad h_{\alpha \alpha }(\alpha ,\ \beta )=4\sin \beta \{-2\sin (2\alpha +\beta)\}=-8\sin \beta \sin (2\alpha +\beta) $
$\quad h_{\alpha \beta }(\alpha ,\ \beta )=4\{\cos \beta (\cos (2\alpha +\beta) - \sin \beta \sin (2\alpha +\beta)\}=4\cos (2\alpha +2\beta) $
$\quad h_{\beta \beta }(\alpha , \ \beta )=4\sin \alpha (-2\sin (\alpha +2\beta))=-8\sin \alpha \sin (\alpha +2\beta) $
$に代入して$
$\quad A=h_{\alpha \alpha }(\cfrac{\pi}{6},\cfrac{\pi}{6})=-4, \quad B=h_{\alpha \beta }(\cfrac{\pi}{6},\cfrac{\pi}{6})=-2, \quad C=h_{\beta \beta }(\cfrac{\pi}{6},\cfrac{\pi}{6})=-4$
$\Delta=B^2-AC=4-16=-12 だから \alpha = \cfrac{\pi}{6} , \quad \beta =\cfrac{\pi}{6} \ \ で極大となり$
$極大値 h=4\sin \cfrac{\pi}{6} \sin \cfrac{\pi}{6} \cos (\cfrac{\pi}{6}+\cfrac{\pi}{6})=\cfrac{1}{2} \ \ をもつ。$
$端点では、h(\alpha ,0)=0,\quad h(0,\beta)=0,\quad h(\cfrac{\pi}{2},\cfrac{\pi}{2})=-4 \ \ だから、極大値は最大値である。$
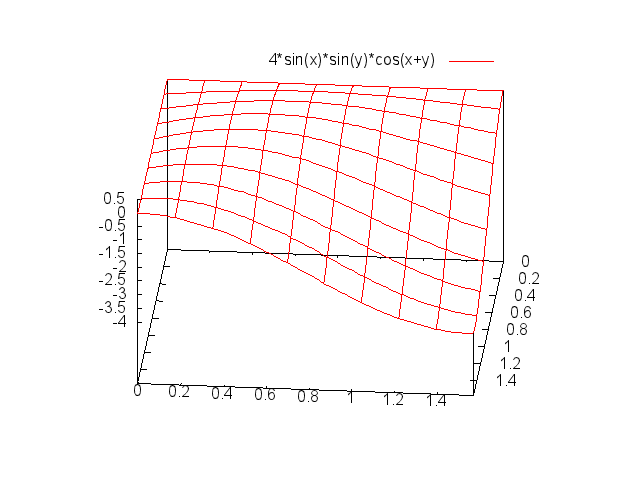
$h(\alpha,\beta)のグラフは下図のとおりです。$
$見にくいのですが、\alpha=\beta=\cfrac{\pi}{6}\fallingdotseq 0.5 で最大となっているのがなんとなくわかります。$
メインメニュー に戻る