転換法
はじめに
『三角形の辺と角の定理』(参照)の中で、$△ABCにおいて$
$\hspace{2em} (1)\quad b > c \quad \longrightarrow ∠B > ∠C$
$\hspace{2em} (2)\quad b = c \quad \longrightarrow ∠B = ∠C$
$\hspace{2em} (3)\quad b < c \quad \longrightarrow ∠B < ∠C$
が成りたつから『転換法』によって、これらの逆も成りたつと述べました。
ここでは、このことについて解説します。
(1)の逆 $∠B > ∠C \quad \longrightarrow \quad b > c $ を背理法で証明します。
$b > c が成りたたないとすると$
$\qquad $(i)$\ \ b=c \hspace{3em}$ (ii)$\ b < c$
のどちらかが成りたちます。
(i)が成りたつならば
上の(2)が成りたつから $∠B = ∠C$ となり、これは$∠B > ∠C$に矛盾します。
(ii)が成りたつならば
上の(3)が成りたつから $∠B < ∠C$ となり、やはり$∠B > ∠C$に矛盾します。
したがって $b > c$ が成りたちます。
(2)の逆 $∠B = ∠C \quad \longrightarrow \quad b = c $ を背理法で証明します。
$b=c が成りたたないとすると$
$\qquad $(i)$\ \ b >c \hspace{3em}$ (ii)$\ \ b < c$
のどちらかが成りたちます。
(i)が成りたつならば
上の(1)が成りたつから $∠B > ∠C$ となり、これは$∠B = ∠C$に矛盾します。
(ii)が成りたつならば
上の(3)が成りたつから $∠B < ∠C$ となり、やはり$∠B = ∠C$に矛盾します。
したがって $b = c$ が成りたちます。
(3)の逆 $∠B < ∠C \quad \longrightarrow \quad b < c $ を背理法で証明します。
$b < c が成りたたないとすると$
$\qquad $(i)$\ \ b=c \hspace{3em}$ (ii)$\ \ b > c$
のどちらかが成りたちます。
(i)が成りたつならば
上の(2)が成りたつから $∠B = ∠C$ となり、これは$∠B < ∠C$に矛盾します。
(ii)が成りたつならば
上の(1)が成りたつから $∠B > ∠C$ となり、やはり$∠B < ∠C$に矛盾します。
したがって $b < c$ が成りたちます。
以上より(1)(2)(3)それぞれの逆が成りたつことがわかりましたので、
あらためて次の定理がいえます。
$定理1 △ABC において$
$\hspace{2em} (1)\ \quad b > c \quad \Longleftrightarrow ∠B > ∠C$
$\hspace{2em} (2)\ \quad b = c \quad \Longleftrightarrow ∠B = ∠C$
$\hspace{2em} (3)\ \quad b < c \quad \Longleftrightarrow ∠B < ∠C$
一般に、
一連の真の命題 $p_1 \longrightarrow q_1,\quad p_2 \longrightarrow q_2,\ \cdots ,\ p_n \longrightarrow q_n$ があって
$(1)\quad 仮定 p_1,p_2,\cdots ,p_n はすべての場合を尽くしている。$
$(2)\quad 結論 q_1,q_2,\cdots ,q_n はどの2つも重なることはない。(両立しない)$
ならば これら一連の命題の逆
$\hspace{4em} q_1 \longrightarrow p_1,\quad q_2 \longrightarrow p_2,\ \cdots , \ q_n \longrightarrow p_n$
が成りたつ。
このような証明法(論理展開)を
『転換法』
といいます。以下、転換法が有効な定理をいくつか掲げます。
定理2 自然数$n$について
$\hspace{2em} (1)\quad p_1 : nは偶数 \quad \Longleftrightarrow q_1 : n^2は偶数$
$\hspace{2em} (2)\quad p_2 : nは奇数 \quad \Longleftrightarrow q_2 : n^2は奇数$
仮定 $p_1,p_2$はすべての場合を尽くしており、結論 $q_1,q_2$は両立しません。
したがって、転換法によりこれらの逆も成りたちます。
逆命題で、何か不安な人は、背理法で証明すればよいでしょう。
$(1)の逆 q_1 : n^2は偶数 \quad \longrightarrow p_1 : nは偶数$ の証明は
$\hspace{2em} n^2は偶数に対して、nは偶数でない、すなわち奇数とすると$
$\hspace{2em} p_2 \quad \longrightarrow q_2 は真だからn^2は奇数となり$
仮定に矛盾する。よって$n$は偶数である。
$(2)の逆 q_2 : n^2は奇数 \quad \longrightarrow p_2 : nは奇数$ の証明は
$\hspace{2em} n^2は奇数に対して、nは奇数でない、すなわち偶数とすると$
$\hspace{2em} p_1 \quad \longrightarrow q_1 は真だからn^2は偶数となり$
仮定に矛盾する。よって$n$は奇数である。
なお、この定理2は、「 $\sqrt{2}$ は無理数である 」の証明に用いられます。
定理3 △ABCにおいて
$\hspace{2em} (1) \quad ∠A < 90°\quad \Longleftrightarrow \quad a^2 < b^2+c^2$
$\hspace{2em} (2) \quad ∠A = 90°\quad \Longleftrightarrow \quad a^2 = b^2+c^2$ (三平方の定理)
$\hspace{2em} (3) \quad ∠A > 90°\quad \Longleftrightarrow \quad a^2 > b^2+c^2$
まず
$\quad (1) \quad ∠A < 90°\quad \longrightarrow \quad a^2 < b^2+c^2$
$\quad (2) \quad ∠A = 90°\quad \longrightarrow \quad a^2 = b^2+c^2$
$\quad (3) \quad ∠A > 90°\quad \longrightarrow \quad a^2 > b^2+c^2$
の証明は
$\hspace{6em}$
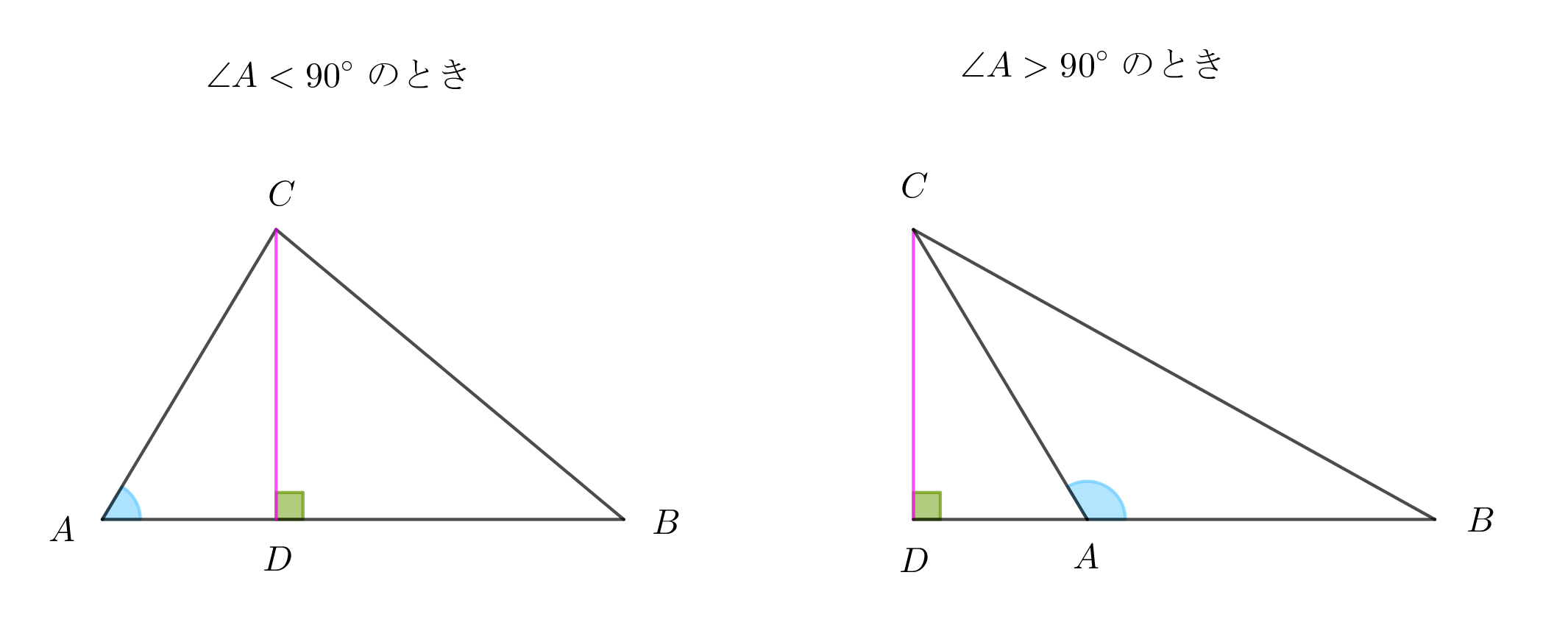
$点Cから辺AC,またはその延長上に垂線を下ろし、足を点D$とする。
$(1) \quad ∠A < 90°\quad \longrightarrow \quad a^2 < b^2+c^2$ の証明
\begin{eqnarray*} BC^2&=&CD^2+DB^2\\ &=&(AC^2-AD^2)+(AB-AD)^2\\ &=&(AC^2-AD^2)+(AB^2-2AB・AD+AD^2)\\ &=&AC^2+AB^2-2AB・AD\\ &<& AC^2+AB^2
\end{eqnarray*} $\quad \therefore \quad a^2 < b^2+c^2$
$(2) \quad ∠A = 90°\quad \longrightarrow \quad a^2 = b^2+c^2$ は三平方の定理です。
$(3) \quad ∠A > 90°\quad \longrightarrow \quad a^2 > b^2+c^2$ の証明
\begin{eqnarray*} BC^2&=&CD^2+DB^2\\ &=&(AC^2-AD^2)+(AB+AD)^2\\ &=&(AC^2-AD^2)+(AB^2+2AB・AD+AD^2)\\ &=&AC^2+AB^2+2AB・AD\\ &>& AC^2+AB^2
\end{eqnarray*} $\quad \therefore \quad a^2 > b^2+c^2$
したがって、転換法によりこれらの逆命題も成りたちます。
定理4
$\quad 直線l上に、2点A,Bがある。lの同じ側でA,Bを角 \alpha に見込む円弧について$
$\hspace{2em} (1) \quad 点Pが円の外側 \quad \Longleftrightarrow \quad ∠APB < \alpha$
$\hspace{2em} (2) \quad 点Pが円の円周上\quad \Longleftrightarrow \quad ∠APB = \alpha$
$\hspace{2em} (3) \quad 点Pが円の内側 \quad \Longleftrightarrow \quad ∠APB > \alpha$
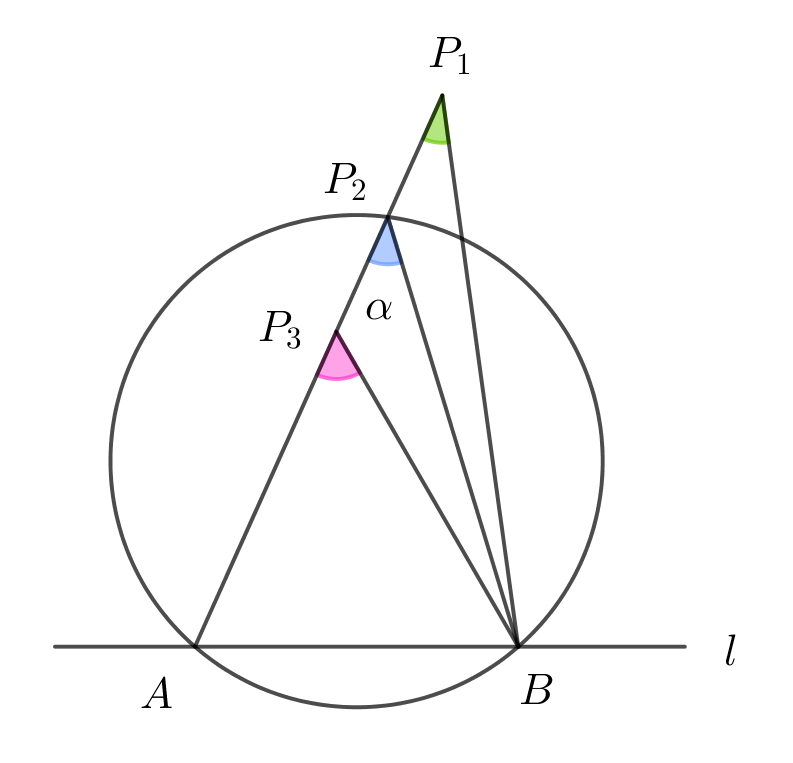
$(1) \quad 点Pが円の外側\quad \longrightarrow \quad ∠APB < \alpha$ の証明は
『三角形の辺と角の定理』の定理4で「三角形の外角は内対角のいずれよりも大きい」を 証明してありますので、(参照)
$\hspace{2em} △P_1P_2Bで、∠P_2P_1B < ∠P_3P_2B$
すなわち $∠AP_1B < \alpha$
$(2) \quad 点Pが円の円周上\quad \longrightarrow \quad ∠APB = \alpha$
$\hspace{2em} は円周角の定理です。$
$(3) \quad 点Pが円の内側\quad \longrightarrow \quad ∠APB > \alpha$ の証明は
$\hspace{2em} △P_2P_3Bで、∠AP_3B > ∠P_3P_2B$
すなわち $∠AP_3B > \alpha$
したがって、転換法によりこれらの逆命題も成りたちます。
定理5 二次方程式 $ax^2+bx+c=0 \quad (a \neq 0)の判別式をDとすると、解は$
$\hspace{2em} (1) \quad D > 0 \quad \Longleftrightarrow \quad 異なる2つの実数解$
$\hspace{2em} (2) \quad D=0 \quad \Longleftrightarrow \quad 重解$
$\hspace{2em} (3) \quad D < 0 \quad \Longleftrightarrow \quad 共役な虚数解$
$(1),(2),(3)の \longrightarrow の証明は二次方程式の解の公式より$
$\hspace{2em} x=\cfrac{-b \pm \sqrt{D}}{2a}$ だから
$D > 0, \ D=0, \ D < 0 のそれぞれに応じて$
異なる2つの実数解、重解、共役な虚数解 をもつ。
したがって、転換法によりこれらの逆も成りたちます。
メインメニュー に戻る