球の表面積
$球を回転体と見たときの表面積の計算方法については$回転体の側面積 $を参考にしてください。$
$ここでは、球の性質をつかった2通りの計算方法について考えてみましょう。$
$(1)\ \ 錐体の体積を利用する方法$
$球面を \ n\ 分割した小球面の面積を \ S_i\ (i=1,\ 2,\ \cdots ,\ n)\ とし、その内部の \ 1\ 点(円とみなせばその中心)と$
$球の中心を結んだ高さ \ r\ の錐体(円錐と考えてよい)を考える。$
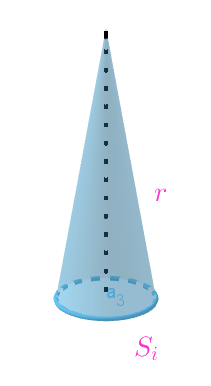
$このとき、n \longrightarrow \infty \quad とするので、小球面は平面とみなすと$
$この錐体の体積は \quad V_i=\cfrac{1}{3}S_i r$
$分割した小球面のすべての和をとると$
\[\sum _i V_i=\cfrac{r}{3}\sum _i S_i\]
$左辺は球の体積V、右辺の和は球の表面積Sだから$
$\quad \cfrac{4}{3}\pi r^3=\cfrac{r}{3}S$
$\quad \therefore \ \ S=4\pi r^2$
$(2)\ \ rの増分に対する体積の増分を利用する方法$
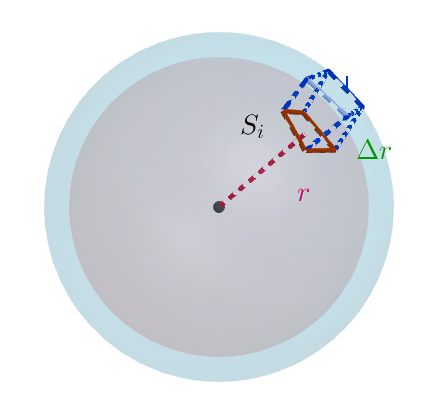
$球面を \ n\ 分割した小球面の面積を \ S_i\ (i=1,\ 2,\ \cdots ,\ n)\ とする。$
$球の半径が \ r\ から \ r+\Delta r \ \ 増加したとき、体積が \ \Delta V\ 増加するとき$
$小球体の体積の増加は、底面積 \ S_i,高さが \ \Delta r \ の直方体と考えて$
$\qquad \Delta V_i=\Delta r \cdot S_i$
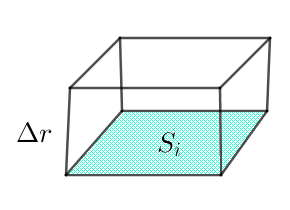
$小球体のすべての和をとると$
\[\sum _i V_i=\Delta r \sum _i S_i\]
\[\sum _i S_i=\cfrac{1}{\Delta r} \sum _i V_i\]
$左辺は球の表面積 \ S\ であり、右辺の和は球の体積の増分だから$
\begin{eqnarray*}
右辺
&=&\cfrac{1}{\Delta r}\big(\cfrac{4}{3}\pi(r+\Delta r)^3-\cfrac{4}{3}\pi r^3\big)\\
&=&\cfrac{4}{3}\pi(3r^2+3r \Delta r +(\Delta r )^2)\\
\end{eqnarray*}
$ここで、\Delta r \longrightarrow 0 \quad とすると \quad S=\cfrac{4}{3}\pi \times 3r^2=4\pi r^2$
メインメニュー に戻る