2次曲線の標準化
$\qquad 座標軸の平行移動・回転移動については($座標軸の平行移動・回転移動$)をご覧ください。$
(1) 2次曲線の回転移動における不変量
$\quad ax^2+2hxy+by^2=c\ \ を原点の回りに \ \theta \ 回転して \ \ AX^2+2HXY+BY^2=C \ \ になったとすると $
$\quad x=X\cos \theta -Y\sin \theta ,\quad y=X\sin \theta +Y\cos \theta \ \ を代入して$
$\quad a(X\cos \theta -Y\sin \theta)^2+2h(X\cos \theta -Y\sin \theta)(X\sin \theta +Y\cos \theta ) +b(X\sin \theta +Y\cos \theta )^2=c$
$\quad (a\cos ^2\theta +2h\sin \theta \cos \theta +b\sin ^2\theta)X^2 +2\{-a\sin \theta \cos \theta +h(\cos ^2\theta-\sin ^2\theta) +b\sin \theta \cos \theta \}XY$
$\hspace{4em} + (a\sin ^2\theta -2h\sin \theta \cos \theta +b\cos ^2\theta)Y^2=c$
$よって$
$\quad A=a\cos ^2\theta +2h\sin \theta \cos \theta +b\sin ^2\theta=a\cos ^2\theta +b\sin ^2\theta +h\sin 2\theta$
$\quad B=a\sin ^2\theta -2h\sin \theta \cos \theta +b\cos ^2\theta =a\sin ^2\theta +b\cos ^2\theta -h\sin 2\theta $
$\quad H=-a\sin \theta \cos \theta +h(\cos ^2\theta-\sin ^2\theta) +b\sin \theta \cos \theta =h\cos 2\theta -\cfrac{a-b}{2}\sin 2\theta $
$このとき$
$\quad A+B=a(\cos ^2\theta +\sin ^2 \theta)+b(\sin ^2\theta+\cos ^2\theta)=a+b$
$\quad A-B=a(\cos ^2\theta -\sin ^2 \theta)+b(\sin ^2\theta -\cos ^2\theta)+2h\sin 2\theta =(a-b)\cos 2\theta +2h\sin 2\theta $
$だから$
\begin{eqnarray*} H^2-AB &=&H^2+\cfrac{1}{4}\{(A-B)^2-(A+B)^2\}\\ &=&\left(h\cos 2\theta -\cfrac{a-b}{2}\sin 2\theta \right)^2 +\cfrac{1}{4}\left[\left\{(a-b)\cos 2\theta +2h\sin 2\theta \ \right\}^2 -(a+b)^2\right]\\ \\ &=&h^2(\cos ^2 2\theta+\sin ^2 2\theta )+\cfrac{(a-b)^2}{4}(\sin^2 2\theta +\cos ^2 2\theta)-\cfrac{1}{4}(a+b)^2\\ \\ &=&h^2-ab\\ \end{eqnarray*}
$これで、回転移動では\ \ A+B \ と \ H^2-AB \ が不変である(保存される)ことがわかりました。$
(2) 2次曲線の分類
$曲線(4)の \ xy \ の項を消去するために座標軸を回転移動したのですが、そのためには \quad H=0 \ \ であればよい。$
$\qquad h\cos 2\theta -\cfrac{a-b}{2}\sin 2\theta =0$
$\qquad \tan \theta =\cfrac{2h}{a-b}$
$を満たす\theta をとればよいことがわかります。ただし、a=b \ \ のときは \ \theta =\cfrac{\pi}{4} \ \ とします。$
$このとき、-AB=h^2-ab ,\qquad (4)は、AX^2+BY^2=C \ \ となります。$
$そこで、D=h^2-ab \ \ とおくと$
(i)$\ \ D<0 \ \ のとき$
$\quad AB>0 \ \ となり、A,\ B \ は同符号$
$\quad A>0 \ \ ととると B>0 \ \ だから \ \ C>0 \ \ ならば楕円を表す。$
(ii)$\ \ D>0 \ \ のとき$
$\quad AB<0 \ \ となり、A,\ B \ \ は異符号$
$\quad A>0 \ \ ととると \ \ B<0 \ \ だから \ \ C \ne 0 \ \ ならば双曲線を表し、C=0 \ \ ならば2直線を表す。$
(iii)$\ \ D=0 \ \ のとき$
$\quad AB=0 \ \ となり、A=0 \ \ または \ \ B=0 \ \ となって放物線を表す。$
$例 x^2-3xy+y^2=1$
$\quad 判別式は \ \ D=(\cfrac{3}{2})^2-1 \times 1=\cfrac{5}{4}\ \ で正だから双曲線である。$
$\quad x^2 \ と \ y^2 \ の係数が等しいので \ \theta=\cfrac{\pi}{4} \ \ とする。$
$\quad x=X\cos \cfrac{\pi}{4}-Y\sin \cfrac{\pi}{4}=\cfrac{X}{\sqrt{2}}-\cfrac{Y}{\sqrt{2}}$
$\quad y=X\sin \cfrac{\pi}{4}+Y\cos \cfrac{\pi}{4}=\cfrac{X}{\sqrt{2}}+\cfrac{Y}{\sqrt{2}}$
$を代入して$
$\quad \left(\cfrac{X}{\sqrt{2}}-\cfrac{Y}{\sqrt{2}}\right)^2-3\left(\cfrac{X}{\sqrt{2}}-\cfrac{Y}{\sqrt{2}}\right)
\left(\cfrac{X}{\sqrt{2}}+\cfrac{Y}{\sqrt{2}}\right)+\left(\cfrac{X}{\sqrt{2}}+\cfrac{Y}{\sqrt{2}}\right)^2=1$
$\quad -\cfrac{1}{2}X^2+\cfrac{5}{2}Y^2=1$
$a+b=1+1=2,\quad A+B=-\cfrac{1}{2}+\cfrac{5}{2}=2 \ \ となって確かに保存されている。$
$整数係数に直すと\quad X^2-5Y^2=-2$
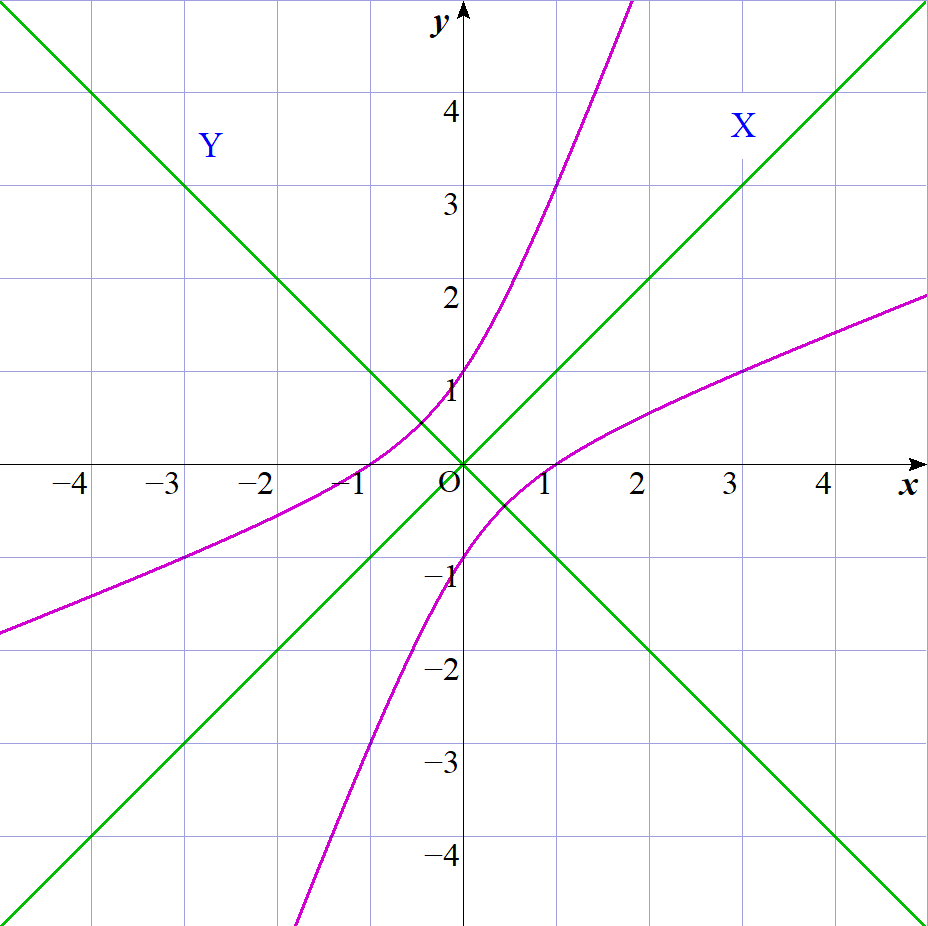
$グラフは右図の通りです。$
2次曲線メニュー に戻る
メインメニュー に戻る