座標軸の平行移動・回転移動
(0) はじめに
$一般に、2次曲線 \ \ f(x,y)=0 \ \ のグラフを描くには、微分法を用いて増減表を作る以外に、平行移動や$
$回転移動を行って、簡単な式に変形する方法があります。$
$その際$
(i)$\ \ 曲線を動かす$
(ii)$\ \ 座標軸を動かす$
$の2通りの方法があります。$
$物理学では、対象物はそのままにして観察、観測する人の目を動かす、すなわち座標軸を動かして$
$見易く、あるいは計算し易くすることが多いと思います。$
$数学は、曲線そのものを動かすこともありますが、私の経験からすると、やはり座標軸を動かした方が$
$後々処理が楽なように思いますが、皆さんはどう思われますか。$
$ここでは、後者の座標軸を動かす手を使って$
$\quad 2次曲線 \ \ f(x,y)=ax^2+2hxy+by^2+cx+dy+e=0 \hspace{15em}(1)$
$の変換不変量などの性質を考えたいと思います。$
(1) 平行移動
$曲線(1)は、x,\ y\ の1次の項を消去するために座標軸を平行移動します。$
$元の座標軸を \ x,\ y\ 軸とし、平行移動する座標軸を \ X,\ Y軸とします。$
$(1)を \ x,\ y\ で偏微分して$
\[ \left\{ \begin{array}{l} f_x(x,y)=2ax+2hy+c=0\\ f_y(x,y)=2hx+2by+d=0\\ \end{array} \right. \] $を解くと$
\[ \left| \begin{array}{cc} a & h\\ h & b\\ \end{array} \right| \ne 0 \quad すなわち h^2-ab \ne 0 \quad のとき解をもつ \] $解を \ \ x=\alpha,\ \ x=\beta \ \ とすると$
$\quad 2a\alpha +2h\beta +c=0,\quad 2h\alpha +2b\beta +d=0 \hspace{15em}(2)$
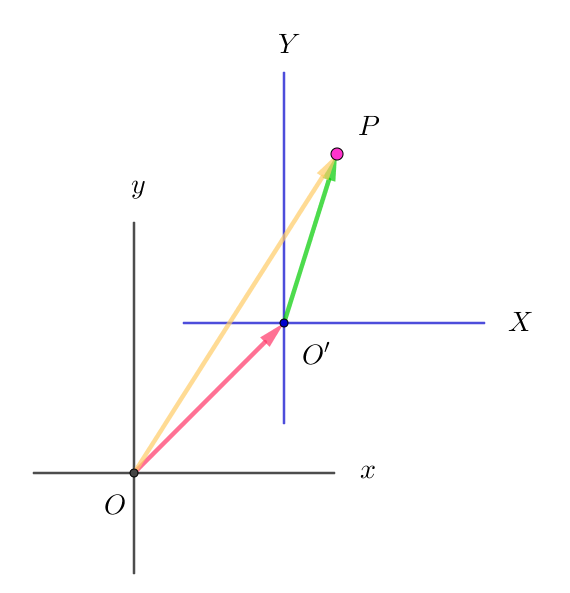
$新座標軸の原点を \ (\alpha,\beta)\ とすると$
$\quad \vec{OP}=\vec{OO'}+\vec{O'P}$
$\quad (x,y)=(\alpha,\beta)+(X,Y)$
$\quad x=X+\alpha,\quad y=Y+\beta$
$このとき(1)は$
$\quad a(X+\alpha )^2+2h(X+\alpha)(Y+\beta)+b(Y+\beta)^2+c(X+\alpha)+d(Y+\beta)+e=0$
$\quad aX^2+2hXY+bY^2+(2a\alpha +2h\beta+c)X+(2b\beta+2h\alpha +d)Y+a\alpha ^2+2h\alpha \beta+b\beta ^2+c\alpha +d\beta +e=0 \hspace{5em}(3)$
$ここで、(2)よりXとYの係数は0となるから、定数項を \ e'\ とおくと$
$\quad aX^2+2hXY+bY^2+e'=0 \hspace{20em}(4)$
$これで、x,\ y\ の1次の項が消えました。$
(2) 回転移動
$(4)のX,Yをあらためてx,yと置きかえると$
$\quad ax^2+2hxy+by^2+e'=0 \hspace{20em}(4')$
$曲線(4')の \ xy \ の項を消去するためには座標軸を回転移動します。$
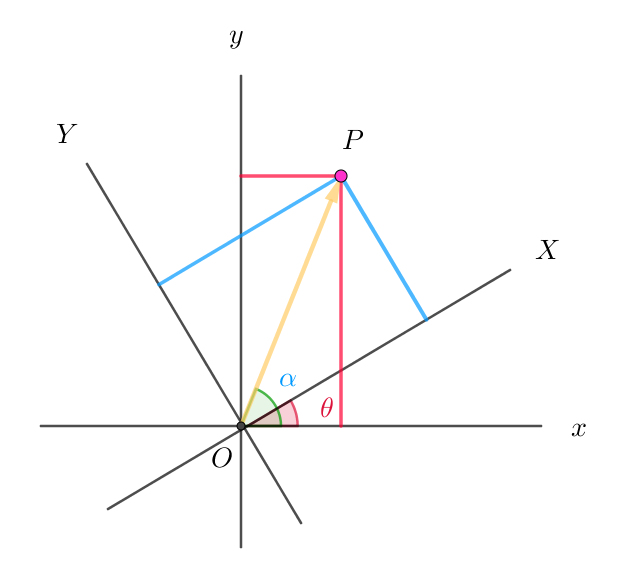
$原点Oを中心に角度 \ \theta \ 回転する座標軸をX,\ Y軸とします。$
$点Pの \ xy\ 座標における座標を(x,y),XY\ 座標における座標を(X,Y),$
$\angle xOP=\alpha,\ \ OP=r \ \ とすると$
$x=r\cos \alpha,\quad y=r\sin \alpha \ \ より$
$X=r\cos (\alpha -\theta)=r\cos \alpha \cos \theta +r\sin \alpha \sin \theta =x\cos \theta +y\sin \theta$
$Y=r\sin (\alpha -\theta)=r\sin \alpha \cos \theta -r\cos \alpha \sin \theta =-x\sin \theta+y\cos \theta$
\[
\left(
\begin{array}{r}
X\\
Y\\
\end{array}
\right)
=
\left(
\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta \\
\end{array}
\right)
\left(
\begin{array}{r}
x\\
y\\
\end{array}
\right)
\]
$逆に解いて$
\[
\left(
\begin{array}{r}
x\\
y\\
\end{array}
\right)
=
\left(
\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta \\
\end{array}
\right)^{-1}
\left(
\begin{array}{r}
X\\
Y\\
\end{array}
\right)
=
\left(
\begin{array}{rr}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta \\
\end{array}
\right)
\left(
\begin{array}{r}
X\\
Y\\
\end{array}
\right)
\]
$x=X\cos \theta -Y\sin \theta ,\qquad y=X\sin \theta +Y\cos \theta$
2次曲線メニュー に戻る
メインメニュー に戻る