信州大学(理系) 2025年　問題7


$実数全体を定義域にもつ \ t\ の関数 \ p\ は微分可能で、すべての \ t\ に対し、\dfrac{dp}{dt} > 0 \ \ を満たすとする。また、p\ の$
$値域は実数全体であるとする。座標平面上において、曲線 \ C:y=\dfrac{e^x+e^{-x}}{2}\ \ 上を運動する点P\ の時刻 \ t\ にお$
$ける座標は \ (p,\ \dfrac{e^p+e^{-p}}{2}\big)\ \ であり、点P\ の速度 \ \vec{u} \ はすべての \ t\ に対し \ \ |\vec{u}|=2\ \ を満たすとする。座標平面上を$
$運動する点Q\ は、時刻 \ t\ において、曲線C\ の点P\ における法線の \ y>\dfrac{e^x+e^{-x}}{2}\ を満たす部分にあり、PQ=1$
$であるとする。t\ が実数全体を動くとき、以下の問いに答えよ。ただし、e\ は自然対数の底である。$
$(1)\ \ 点Q\ の座標を \ p\ を用いて表せ。$
$(2)\ \ 点Q\ の速度を \ \vec{v}\ とするとき、|\vec{v}|\ \ のとり得る値の範囲を求めよ。$


(1)

　

$点P(p,\ r),\ \ Q(q,\ s)\ \ とすると、r= \dfrac{e^p+e^{-p}}{2}$

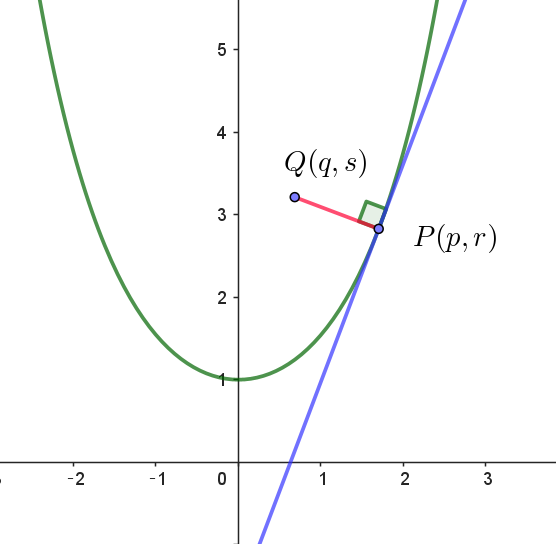
$C:y=\dfrac{e^x+e^{-x}}{2} \ \ について \quad y'=\dfrac{e^x-e^{-x}}{2} \quad だから$

$法線 \ PQ\ の傾きは \quad \dfrac{s-r}{q-p}=-\dfrac{2}{e^p-e^{-p}} \hspace{5em}①$

$s-r =-\dfrac{2}{e^p-e^{-p}}(q-p) \hspace{12em}②$

$PQ^2=(q-p)^2+(s-r)^2=1 \quad に代入して$

$(q-p)^2+\big(-\dfrac{2}{e^p-e^{-p}}\big)^2 (q-p)^2=1$

$(q-p)^2\big\{1+\dfrac{4}{(e^p-e^{-p})^2}\big\} =1$

$(q-p)^2 \times \dfrac{(e^p-e^{-p})^2+4}{(e^p-e^{-p})^2} =1$

$(q-p)^2 =\dfrac{(e^p-e^{-p})^2}{(e^p-e^{-p})^2+4}=\dfrac{(e^p-e^{-p})^2}{(e^p+e^{-p})^2}$

$ここで、点Q\ は、点P\ における法線の \ y>\dfrac{e^x+e^{-x}}{2}\ を満たす部分にあるから \quad s > r$

$したがって①より \quad q-p \ \ と \ \ -(e^p-e^{-p})\ \ の符号は一致する。$

$ゆえに \quad q-p =-\dfrac{e^p-e^{-p}}{e^p+e^{-p}}$

$q=p -\dfrac{e^p-e^{-p}}{e^p+e^{-p}}$

$②に代入して$

\begin{eqnarray*} s &=&r -\dfrac{2}{e^p-e^{-p}}(q-p)\\ \\ &=&\dfrac{e^p+e^{-p}}{2} - \dfrac{2}{e^p-e^{-p}} \times \big(-\dfrac{e^p-e^{-p}}{e^p+e^{-p}}\big)\\ \\ &=&\dfrac{e^p+e^{-p}}{2} + \dfrac{2}{e^p+e^{-p}} \end{eqnarray*}
$したがって \quad Q\big(p -\dfrac{e^p-e^{-p}}{e^p+e^{-p}}, \ \ \dfrac{e^p+e^{-p}}{2} + \dfrac{2}{e^p+e^{-p}}\big)$


(2)


$r=\dfrac{e^p+e^{-p}}{2} ,\quad \vec{u}=\big(\dfrac{dp}{dt},\dfrac{dr}{dt}\big)$

$\dfrac{dr}{dt}=\dfrac{dr}{dp} \cdot \dfrac{dp}{dt}=\dfrac{e^p-e^{-p}}{2} \cdot \dfrac{dp}{dt}$

\begin{eqnarray*} |\vec{u}|^2 &=&\big(\dfrac{dp}{dt}\big)^2+\big(\dfrac{dr}{dt}\big)^2\\ \\ &=&\big(\dfrac{dp}{dt}\big)^2+ \big( \dfrac{e^p-e^{-p}}{2} \cdot \dfrac{dp}{dt}\big)^2\\ \\ &=&\big\{1+ \big( \dfrac{e^p-e^{-p}}{2} \big)^2\big\} \big( \dfrac{dp}{dt}\big)^2\\ \\ &=&\dfrac{(e^p+e^{-p})^2}{4} \big( \dfrac{dp}{dt}\big)^2\\ \end{eqnarray*}
$|\vec{u}|=2 ,\quad \dfrac{dp}{dt} > 0 \quad だから \quad \dfrac{dp}{dt}=\dfrac{4}{e^p+e^{-p}}$

$これを踏まえて$

$q=p -\dfrac{e^p-e^{-p}}{e^p+e^{-p}}\quad より \quad \dfrac{dq}{dp}=1-\dfrac{(e^p+e^{-p})^2-(e^p-e^{-p})^2}{(e^p+e^{-p})^2}=1-\dfrac{4}{(e^p+e^{-p})^2}$

$s=\dfrac{e^p+e^{-p}}{2} + \dfrac{2}{e^p+e^{-p}} \quad より \quad \dfrac{ds}{dp}=\dfrac{e^p-e^{-p}}{2} - \dfrac{2(e^p-e^{-p})}{(e^p+e^{-p})^2}=\dfrac{e^p-e^{-p}}{2} \big(1- \dfrac{4}{(e^p+e^{-p})^2}\big)=\dfrac{e^p-e^{-p}}{2} \cdot \dfrac{dq}{dp}$
\begin{eqnarray*}
|\vec{v}|^2 &=&\big(\dfrac{dq}{dt}\big)^2+\big(\dfrac{ds}{dt}\big)^2\\ \\ &=&\big(\dfrac{dq}{dp} \cdot \dfrac{dp}{dt}\big)^2+\big(\dfrac{ds}{dp} \cdot \dfrac{dp}{dt}\big)^2\\ \\ &=&\big\{\big(\dfrac{dq}{dp}\big)^2 + \big(\dfrac{ds}{dp}\big)^2 \big\} \big(\dfrac{dp}{dt}\big)^2\\ \\ &=&\big\{\big(\dfrac{dq}{dp}\big)^2 + \big(\dfrac{e^p-e^{-p}}{2} \cdot \dfrac{dq}{dp}\big)^2 \big\} \big(\dfrac{dp}{dt}\big)^2\\ \\ &=&\big\{1+\big(\dfrac{e^p-e^{-p}}{2}\big)^2\big\} \big(\dfrac{dq}{dp}\big)^2 \big(\dfrac{dp}{dt}\big)^2\\ \\ &=&\dfrac{(e^p+e^{-p})^2}{4} \times \big\{1-\dfrac{4}{(e^p+e^{-p})^2 }\big\}^2 \big(\dfrac{dp}{dt}\big)^2\\ \\ &=&\dfrac{(e^p+e^{-p})^2}{4} \times \dfrac{(e^p+e^{-p})^2 -4}{(e^p+e^{-p})^2} \big(\dfrac{dp}{dt}\big)^2\\ \\ &=&\dfrac{(e^p-e^{-p})^2}{4} \big(\dfrac{dp}{dt}\big)^2\\ \end{eqnarray*}
$|\vec{v}|=\dfrac{|e^p-e^{-p}|}{2}\dfrac{dp}{dt}=\dfrac{|e^p-e^{-p}|}{2} \times \dfrac{4}{e^p+e^{-p}}=\dfrac{2|e^p-e^{-p}|}{e^p+e^{-p}}$

\[|\vec{v}|= \hspace{1em} \left\{ \begin{array}{l} -\dfrac{2(e^p-e^{-p})}{e^p+e^{-p}} \hspace{5em}(p \leqq 0 \ \ のとき)\\ \\ \dfrac{2(e^p-e^{-p})}{e^p+e^{-p}} \hspace{6em}(p >0 \ \ のとき)\\ \end{array} \right. \]
$f(p)=\dfrac{2(e^p-e^{-p})}{e^p+e^{-p}} \quad とおくと \quad f(p)=2-\dfrac{4e^{-p}}{e^p+e^{-p}}=2-\dfrac{4}{e^{2p}+1}$

$f'(p)=-4 \times \dfrac{(-2e^{2p})}{(e^{2p}+1)^2}=\dfrac{8e^{2p}}{(e^{2p}+1)^2} > 0$

$f(p)\ は単調増加で \quad f(0)=0$

$p \longrightarrow \infty \quad とすると \quad f(p) \longrightarrow 2$

$|\vec{v}|=F(p) \quad とおくと$

　

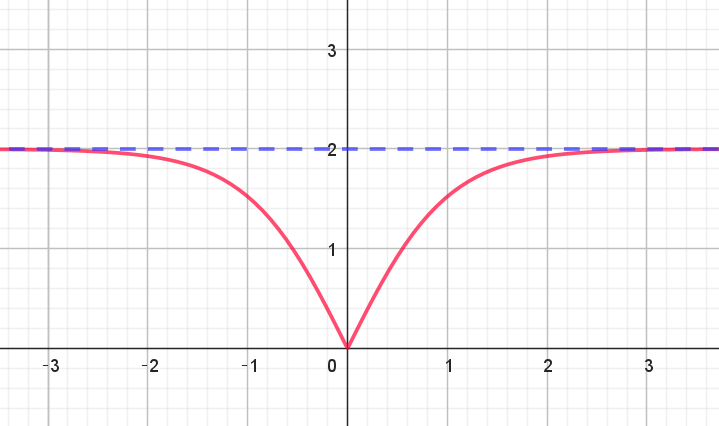
$F(-p)=\dfrac{2|e^{-p}-e^p|}{e^{-p}+e^p}=\dfrac{2|e^p-e^{-p}|}{e^p+e^{-p}}=F(p)$

$よって、F(p)\ は偶関数でこのグラフは右図のとおり$

$|\vec{v}|\ \ のとり得る値の範囲は \quad 0 \leqq |\vec{v}| <2 $


$(補充)$

$曲線 \ C:y=\dfrac{e^x+e^{-x}}{2} \ \ は双曲線関数とよばれています。$

$詳しくは($双曲線関数$)をご覧ください。$


ページの先頭へ↑



メインメニュー　に戻る