双曲線関数


１　双曲線関数とは

　

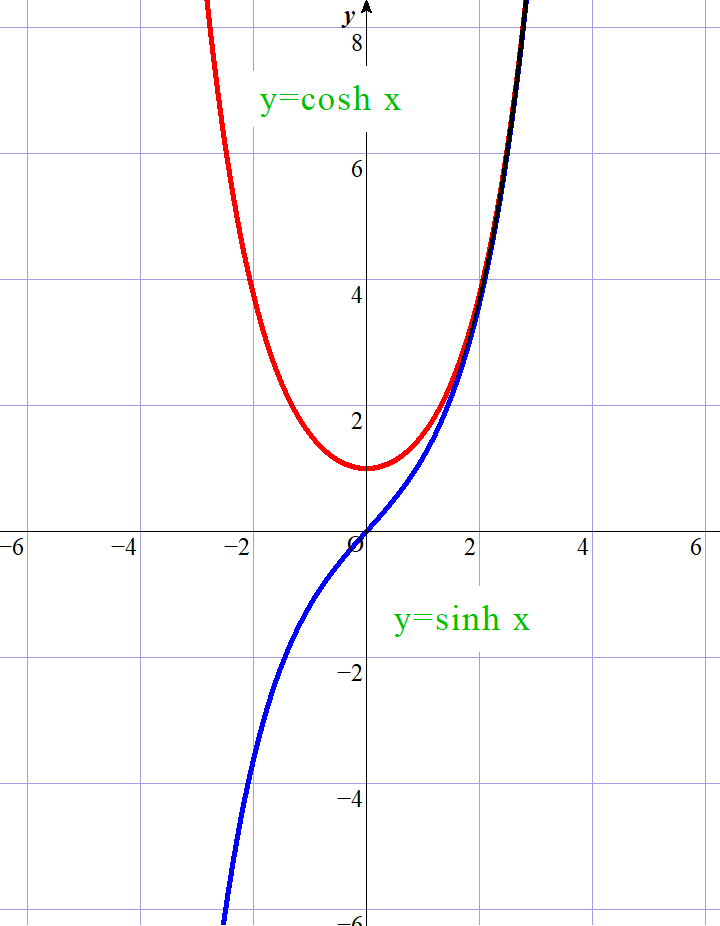
$y=\cfrac{e^x-e^{-x}}{2},\ \ y=\cfrac{e^x+e^{-x}}{2}\ \ を双曲線関数といい、$

$それぞれ　y=\sinh x , \ \ y=\cosh x \ \ と表し,$

$ハイパボリックサイン,ハイパボリックコサインと読みます。$

$すなわち$

$\quad \sinh x=\cfrac{e^x-e^{-x}}{2},\quad \cosh x=\cfrac{e^x+e^{-x}}{2}$

$グラフはそれぞれ右図のとおりです。$

$y=\cosh x 　はカテナリー(懸垂線)とよばれています。$

2　名前の由来


$この関数については、名前と記号ですぐに疑問がわきます。$

(i)$\ グラフは双曲線に似ても似つかないのに、なぜ双曲線関数というのでしょうか。$

(ii)$ なぜ、\sinh, \ \ \cosh \ \ とかくのでしょうか。三角関数と関係があるのでしょうか。$

$勝手に私なりの考えを述べます。$

$まず、$(i)$についてですが、$

$\quad 点P(\cosh t ,\ \sinh t) \ は$
\begin{eqnarray*} x^2-y^2 &=&\big(\cfrac{e^t + e^{-t}}{2}\big)^2-\big(\cfrac{e^t - e^{-t}}{2}\big)^2\\ \\ &=&\cfrac{e^{2t}+2+e^{-2t}}{4}-\cfrac{e^{2t}-2+e^{-2t}}{4}\\ \\ &=&1\\ \end{eqnarray*} $よって、双曲線 \ \ x^2-y^2=1 \ \ 上の点です。$

$おそらくこのようなことから双曲線関数とネーミングされたのではないでしょうか。$


$次に、$(ii)$についてですが、$

$\sinh x ,\ \ \cosh x \ \ は次に示すように三角関数の \ \ \sin x ,\ \ \cos x \ \ と類似の公式が導かれますので$
$この記号が使われたと思います。$


3　双曲線関数の公式


$(1)\ 平方の差$
\begin{eqnarray*} \cosh ^2x - \sinh ^2x &=&\big(\cfrac{e^x+e^{-x}}{2}\big)^2-\big(\cfrac{e^x-e^{-x}}{2}\big)^2\\ \\ &=&\cfrac{1}{4}(e^{2x}+2+e^{-2x})-\cfrac{1}{4}(e^{2x}-2+e^{-2x})\\ \\ &=&1\\ \end{eqnarray*}
$(2)\ 2倍角の公式$
\begin{eqnarray*} \sinh 2x &=& \cfrac{e^{2x}-e^{-2x}}{2}\\ \\ &=&\cfrac{(e^x-e^{-x})(e^x+e^{-x})}{2}\\ \\ &=&2\sinh x\ \cosh x\\ \end{eqnarray*}
\begin{eqnarray*} \cosh 2x &=&\cfrac{e^{2x}+e^{-2x}}{2}\\ \\ &=&\cfrac{(e^x+e^{-x})^2-2}{2}\\ \\ &=&2\big(\cfrac{e^{x}+e^{-x}}{2}\big)^2-1\\ \\ &=&2\cosh ^2x-1\\ \end{eqnarray*}
$(3)\ 加法定理$
\begin{eqnarray*} \sinh (x+y) &=&\cfrac{e^{x+y}-e^{-(x+y)}}{2}\\ \\ &=&\cfrac{1}{4}\{(e^x-e^{-x})(e^y+e^{-y})+(e^x+e^{-x})(e^y-e^{-y})\}\\ \\ &=&\sinh x\ \cosh y + \cosh x\ \sinh y\\ \end{eqnarray*}
\begin{eqnarray*} \cosh (x+y) &=&\cfrac{e^{x+y}+e^{-(x+y)}}{2}\\ \\ &=&\cfrac{1}{4}\{(e^x+e^{-x})(e^y+e^{-y})+(e^x-e^{-x})(e^y-e^{-y})\}\\ \\ &=&\cosh x\ \cosh y + \sinh x\ \sinh y\\ \end{eqnarray*}
$(4)\ 3倍角$

\begin{eqnarray*} \sinh 3x &=&\sinh (2x+x)\\ \\ &=&\sinh 2x\ \cosh x + \cosh 2x\ \sinh x\\ \\ &=&2\sinh x\ \cosh ^2x + (2\cosh ^2x-1)\ \sinh x\\ \\ &=&2\sinh x\ (\sinh ^2 x+1) + (2\sinh ^2x+1)\ \sinh x\\ \\ &=&4\sinh ^3x + 3\sinh x\\ \end{eqnarray*}
\begin{eqnarray*} \cosh 3x &=&\cosh (2x+x)\\ \\ &=&\cosh 2x\ \cosh x + \sinh 2x\ \sinh x\\ \\ &=&(2\cosh ^2x-1)\cosh x + 2\sinh ^2x \ \cosh x\\ \\ &=&2\cosh ^3 x- \cosh x + 2(\cosh ^2x-1)\ \cosh x\\ \\ &=&4\cosh ^3x - 3\cosh x\\ \end{eqnarray*}

$(4)\ 導関数$

$\qquad (\sinh x)'=(\cfrac{e^{x}-e^{-x}}{2})'=\cfrac{e^{x}+e^{-x}}{2}=\cosh x$

$\qquad (\cosh x)'=(\cfrac{e^{x}+e^{-x}}{2})'=\cfrac{e^{x}-e^{-x}}{2}=\sinh x$


$双曲線関数は、自然科学や工学で必須の関数ですが、この原稿は、3\ 次方程式を解くために$
$書きましので、公式はこのくらいで一応やめます。$
$是非$ 3次方程式の実数解を求める方法$を訪れてください。$




ページの先頭へ↑



メインメニュー　に戻る