流体の連続方程式
$パイプの中を水が連続的に流れている。ただし、パイプの断面積は一定とは限らないし、水が流れる速度も$
$必ずしも一定とは限りません。$
$この水の流れる様子を2通りの方法でとらえましょう。$
$(1)\ \ 時間の差でみた場合$

$時刻tで、位置xでの単位長さ当たりの$
$流体の質量をP(x,t)とする。$
$区間 \Delta x内の流体の質量は$
$時刻 \ t \ で \ P(x,t)\Delta x ,$
$時刻 \ t+\Delta t\ で \ P(x,t+\Delta t)\Delta x \ \ だから$
$\Delta t時間における変化量は$
$\qquad P(x,t+\Delta t)\Delta x-P(x,t)\Delta x \fallingdotseq \cfrac{\partial P}{\partial t}\Delta t \Delta x$
$(2)\ \ 位置の差でみた場合$
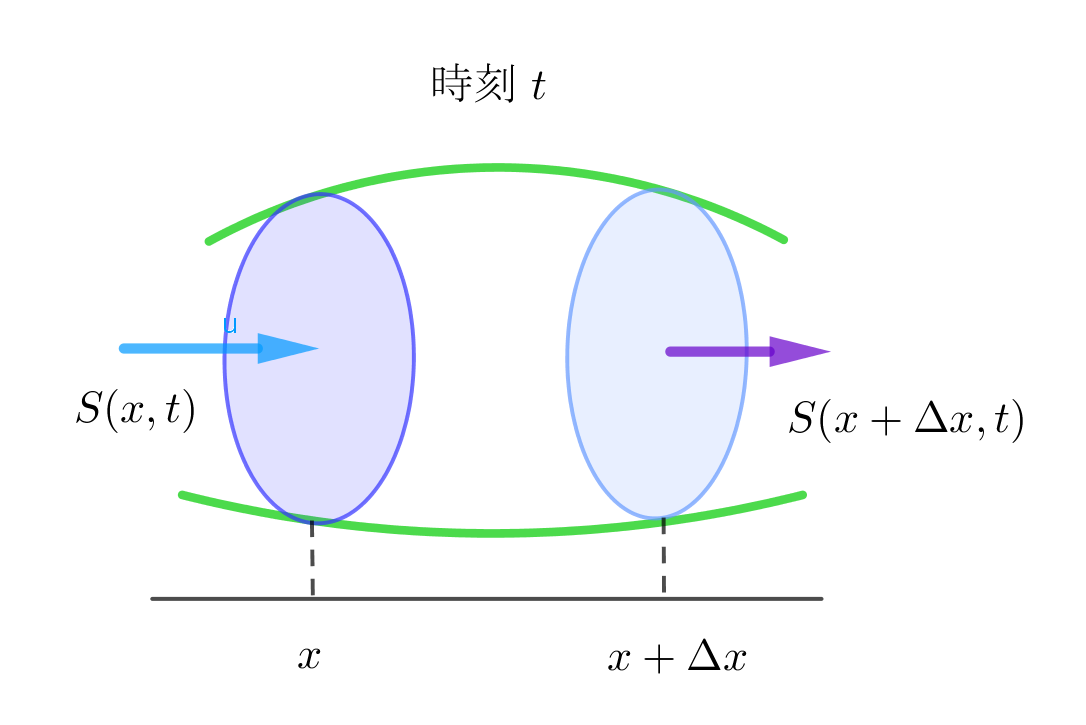
$時刻tで、位置xでの単位時間当たりの$
$流体の流入量をS(x,t)とすると、\Delta t 時間では$
$\qquad S(x,t)\Delta t$
$流出量は\ \ S(x+\Delta x,t)\Delta t \ \ だから$
$区間 \Delta x内に蓄えられる質量は$
$\qquad S(x,t)\Delta t- S(x+\Delta x,t)\Delta t \fallingdotseq -\cfrac{\partial S}{\partial x}\Delta x \Delta t$
$(1)と(2)は同じ量だから$
$\qquad \cfrac{\partial P}{\partial t}\Delta t \Delta x=-\cfrac{\partial S}{\partial x}\Delta x\Delta t$
$\qquad \therefore \cfrac{\partial S}{\partial x}+\cfrac{\partial P}{\partial t}=0$
$これは、湧き出しのない流体の質量保存を表した「連続方程式」と呼ばれています。$
メインメニュー に戻る