トンネル効果
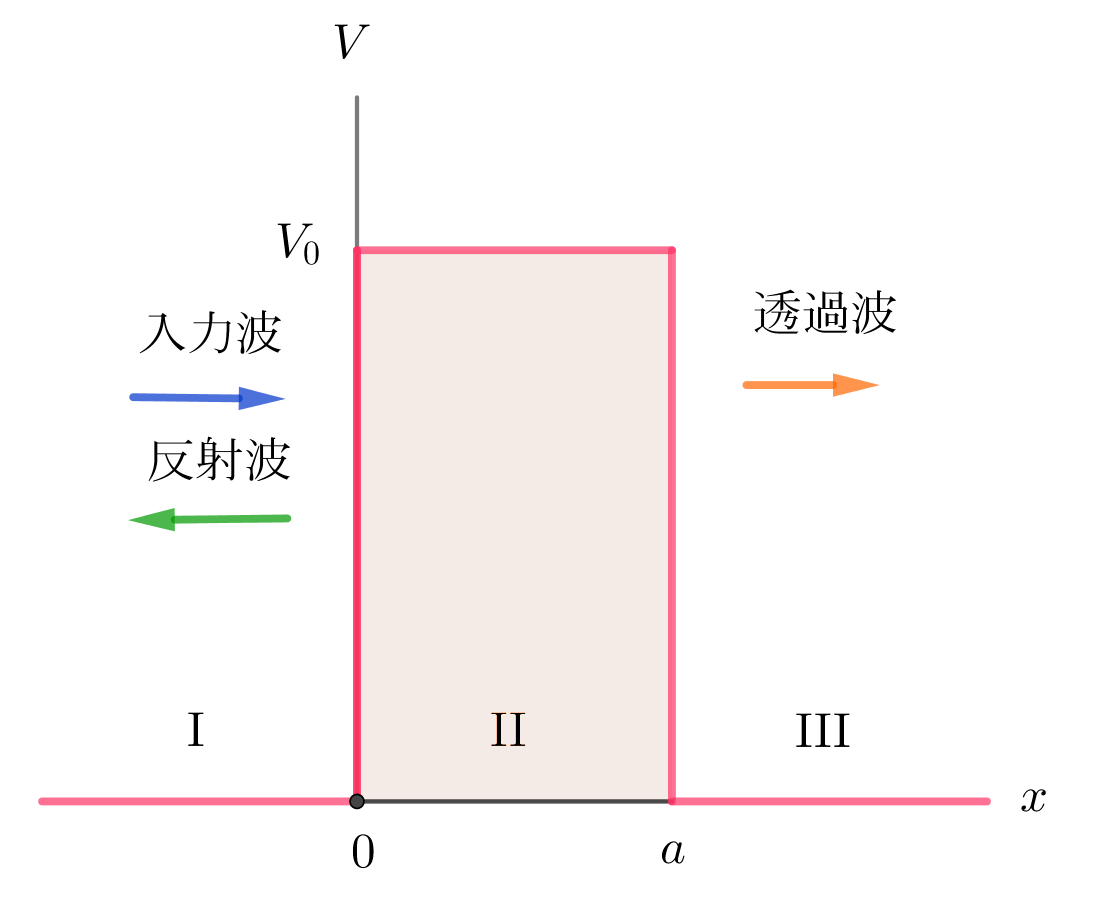
$右図は有限な高さの壁のポテンシャルです。$
$V_0 > 0 \ として$
\[V(x)=
\left\{ \begin{array}{l}
0 \hspace{3em} (x < 0,\ \ x > a)\\
V_0 \hspace{3em} (0 \leqq x \leqq a )\\
\end{array} \right.
\]
$を考えます。$
$左から壁に向かって入射された、エネルギーE \ \ (0 < E < V_0 )\ の$
$量子は、壁で反射される量子もあれば、壁を透過する量子があります。$
$ここでは透過する量子について考えてみましょう。$
$まずはシュレディンガー方程式を解きます。$
$(1)\ \ 領域Ⅰでは$
$\qquad -\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}\varphi(x)=E\varphi(x)\ \ より \cfrac{d^2 }{dx^2}\varphi(x)=-\cfrac{2mE}{\hbar ^2} \varphi(x)$
$\qquad \alpha=\cfrac{\sqrt{2mE}}{\hbar}\ \ とおくと \qquad \cfrac{d^2 }{dx^2}\varphi(x)=-\alpha ^2 \varphi(x)$
$\quad 入射波と反射波が存在するから$
$\qquad \varphi_1(x)=Ae^{i\alpha x}+Be^{-i\alpha x}$
$(2)\ \ 領域Ⅱでは$
$\qquad -\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}\varphi(x)+V_0\varphi(x)=E\varphi(x) \ \ より \cfrac{d^2 }{dx^2}\varphi(x)=\cfrac{2m(V_0-E)}{\hbar ^2} \varphi(x)$
$\qquad \beta=\cfrac{\sqrt{2m(V_0-E)}}{\hbar} \ \ とおくと \qquad \cfrac{d^2 }{dx^2}\varphi(x)=\beta ^2 \varphi(x)$
$\qquad \varphi_2(x)=Ce^{\beta x}+De^{-\beta x}$
$(3)\ \ 領域Ⅲでは$
$シュレディンガー方程式は領域Ⅰと同じで$
$\qquad \cfrac{d^2 }{dx^2}\varphi(x)=-\alpha ^2 \varphi(x)$
$\quad 右への進行波だけだから$
$\qquad \varphi_3(x)=Fe^{i\alpha x}$
$これらの接続条件は$
$\quad \varphi_1(0)=\varphi_2(0)\ \ より A+B=C+D \hspace{18em}(1)$
$\quad \varphi_1'(0)=\varphi_2'(0)\ \ より Ai\alpha -Bi\alpha =C\beta -D\beta \hspace{15em}(2)$
$\quad \varphi_2(a)=\varphi_3(a)\ \ より Ce^{\beta a}+De^{-\beta a} =Fe^{i\alpha a} \hspace{15em}(3)$
$\quad \varphi_2'(a)=\varphi_3'(a)\ \ より C\beta e^{\beta a}-D\beta e^{-\beta a} =Fi\alpha e^{i\alpha a} \hspace{13em}(4)$
$これらを行列で表すと$
$(1)(2)より \qquad
\left(
\begin{array}{rr}
1 & 1 \\
i\alpha & -i\alpha \\
\end{array}
\right)
\left(
\begin{array}{r}
A \\
B \\
\end{array}
\right)
=
\left(
\begin{array}{rr}
1 & 1 \\
\beta & -\beta \\
\end{array}
\right)
\left(
\begin{array}{r}
C \\
D \\
\end{array}
\right) \hspace{11em}(5)$
$(3)(4)より \qquad
\left(
\begin{array}{rr}
e^{\beta a} & e^{-\beta a} \\
\beta e^{\beta a}& -\beta e^{-\beta a} \\
\end{array}
\right)
\left(
\begin{array}{r}
C \\
D \\
\end{array}
\right)
=
\left(
\begin{array}{r}
e^{i\alpha a }\\
i\alpha e^{i\alpha a} \\
\end{array}
\right)
\begin{array}{r}
F \\
\end{array}
\hspace{11em}(6)$
$(5)(6)より \left(
\begin{array}{r}
C \\
D \\
\end{array}
\right)
を消去すると$
$\qquad \left(
\begin{array}{r}
A \\
B \\
\end{array}
\right)
=
\left(
\begin{array}{rr}
1 & 1 \\
i\alpha & -i\alpha \\
\end{array}
\right)^{-1}
\left(
\begin{array}{rr}
1 & 1 \\
\beta & -\beta \\
\end{array}
\right)
\left(
\begin{array}{rr}
e^{\beta a} & e^{-\beta a} \\
\beta e^{\beta a} & -\beta e^{-\beta a} \\
\end{array}
\right)^{-1}
\left(
\begin{array}{r}
e^{i\alpha a }\\
i\alpha e^{i\alpha a} \\
\end{array}
\right)
\begin{array}{r}
F \\
\end{array}
$
$右辺の行列の積をPとおくと$
\begin{eqnarray*}
P
&=&\cfrac{1}{2i\alpha}
\left(
\begin{array}{rr}
i\alpha & 1 \\
i\alpha & -1 \\
\end{array}
\right)
\left(
\begin{array}{rr}
1 & 1 \\
\beta & -\beta \\
\end{array}
\right)
\cfrac{1}{2\beta }
\left(
\begin{array}{rr}
\beta e^{-\beta a} & e^{-\beta a} \\
\beta e^{\beta a} & -e^{\beta a} \\
\end{array}
\right)
\left(
\begin{array}{r}
e^{i\alpha a }\\
i\alpha e^{i\alpha a} \\
\end{array}
\right)
\\
\\
&=&\cfrac{1}{4i\alpha \beta}
\left(
\begin{array}{rr}
\beta + i\alpha & -\beta +i\alpha \\
-\beta + i\alpha & \beta +i\alpha \\
\end{array}
\right)
\left(
\begin{array}{r}
\beta e^{-\beta a+i\alpha a} + i\alpha e^{-\beta a+i\alpha a} \\
\beta e^{\beta a+i\alpha a} - i\alpha e^{\beta a+i\alpha a} \\
\end{array}
\right)
\\
\\
&=&\cfrac{1}{4i\alpha \beta}
\left(
\begin{array}{r}
(\beta + i\alpha)(\beta e^{-\beta a+i\alpha a} + i\alpha e^{-\beta a+i\alpha a})+(-\beta +i\alpha)(\beta e^{\beta a+i\alpha a} - i\alpha e^{\beta a+i\alpha a}) \\
(-\beta + i\alpha)(\beta e^{-\beta a+i\alpha a} + i\alpha e^{-\beta a+i\alpha a})+(\beta +i\alpha)(\beta e^{\beta a+i\alpha a} - i\alpha e^{\beta a+i\alpha a}) \\
\end{array}
\right)
\\
\\
&=&\cfrac{1}{4i\alpha \beta}
\left(
\begin{array}{r}
\{(\alpha ^2-\beta ^2)(e^{\beta a}-e^{-\beta a})+2i\alpha \beta (e^{\beta a}+e^{-\beta a})\}e^{i\alpha a}\\
(\alpha ^2+\beta ^2)(e^{\beta a}-e^{-\beta a})e^{i\alpha a}\\
\end{array}
\right)
\\
\\
&=&\cfrac{1}{4i\alpha \beta}
\left(
\begin{array}{r}
\left\{2(\alpha ^2-\beta ^2)\times \cfrac{e^{\beta a}-e^{-\beta a}}{2}+4i\alpha \beta \times \cfrac{e^{\beta a}+e^{-\beta a}}{2}\right\}e^{i\alpha a}\\
2(\alpha ^2+\beta ^2)\big(\cfrac{e^{\beta a}-e^{-\beta a}}{2}\big)e^{i\alpha a}\\
\end{array}
\right)
\\
\\
&=&\cfrac{1}{4i\alpha \beta}
\left(
\begin{array}{r}
\{2(\alpha ^2-\beta ^2)\sinh \beta a +4i\alpha \beta \cosh \beta a \}e^{i\alpha a}\\
2(\alpha ^2+\beta ^2)\sinh \beta a \ e^{i\alpha a}\\
\end{array}
\right)
\\
\\
&=&
\left(
\begin{array}{r}
\big(\cosh \beta a +i\cfrac{\beta ^2 -\alpha ^2}{2\alpha \beta} \sinh \beta a \big)e^{i\alpha a}\\
-i\cfrac{\alpha ^2+\beta ^2}{2\alpha \beta }\sinh \beta a \ e^{i\alpha a}\\
\end{array}
\right)
\\
\\
\end{eqnarray*}
$\qquad 透過率=\cfrac{透過波のS}{入射波のS}=\cfrac{\cfrac{\hbar \alpha}{m}|F|^2}{\cfrac{\hbar \alpha}{m}|A|^2}=\cfrac{|F|^2}{|A|^2}$
$よって、量子がポテンシャル障壁を透過する割合Tは$
\[
T=\left |\cfrac{F}{A} \right |^2=\left |\cfrac{e^{-i\alpha a}}{\cosh \beta a +i\cfrac{\beta ^2 -\alpha ^2}{2\alpha \beta} \sinh \beta a } \right |^2
=\cfrac{1}{\cosh ^2 \beta a +\big(\cfrac{\beta ^2 -\alpha ^2}{2\alpha \beta}\big)^2 \sinh ^2 \beta a }\\
\]
$ここで、\cosh ^2 t - \sinh ^2 t=1 \ \ だから$ (双曲線関数参照)
\begin{eqnarray*}
T
&=&\cfrac{1}{1+\sinh ^2 \beta a +\big(\cfrac{\beta ^2 -\alpha ^2}{2\alpha \beta}\big)^2 \sinh ^2 \beta a }\\
\\
&=&\cfrac{1}{1+\left \{1+\big(\cfrac{\beta ^2 -\alpha ^2}{2\alpha \beta}\big)^2\right \} \sinh ^2 \beta a }\\
\\
&=&\cfrac{1}{1+\big(\cfrac{\beta ^2 +\alpha ^2}{2\alpha \beta}\big)^2 \sinh ^2 \beta a }\\
\end{eqnarray*}
$\qquad \alpha=\cfrac{\sqrt{2mE}}{\hbar} ,\quad \beta=\cfrac{\sqrt{2m(V_0-E)}}{\hbar}= \sqrt{\cfrac{2mV_0}{\hbar ^2}\big(1-\cfrac{E}{V_0}\big)} \ \ を代入して$
$\qquad \alpha ^2+\beta ^2=\cfrac{2mE}{\hbar ^2}+\cfrac{2mV_0}{\hbar ^2}\big(1-\cfrac{E}{V_0}\big)=\cfrac{2mV_0}{\hbar ^2}$
$\qquad \alpha \beta =\sqrt{\cfrac{2mE}{\hbar ^2}}\times \sqrt{\cfrac{2mV_0}{\hbar ^2}\big(1-\cfrac{E}{V_0}\big)}=\cfrac{2m}{\hbar ^2}\sqrt{V_0E(1-\cfrac{E}{V_0})}$
\begin{eqnarray*}
Tの分母
&=&1+\Biggl(\cfrac{\cfrac{2mV_0}{\hbar ^2}}{2\times \cfrac{2m}{\hbar ^2}\sqrt{V_0E(1-\cfrac{E}{V_0})}}\Biggr)^2\sinh ^2 \beta a\\
\\
&=&1+\cfrac{\sinh ^2 a \sqrt{\cfrac{2mV_0}{\hbar ^2}\big(1-\cfrac{E}{V_0}\big)}}{\cfrac{4E}{V_0}(1-\cfrac{E}{V_0})}\\
\end{eqnarray*}
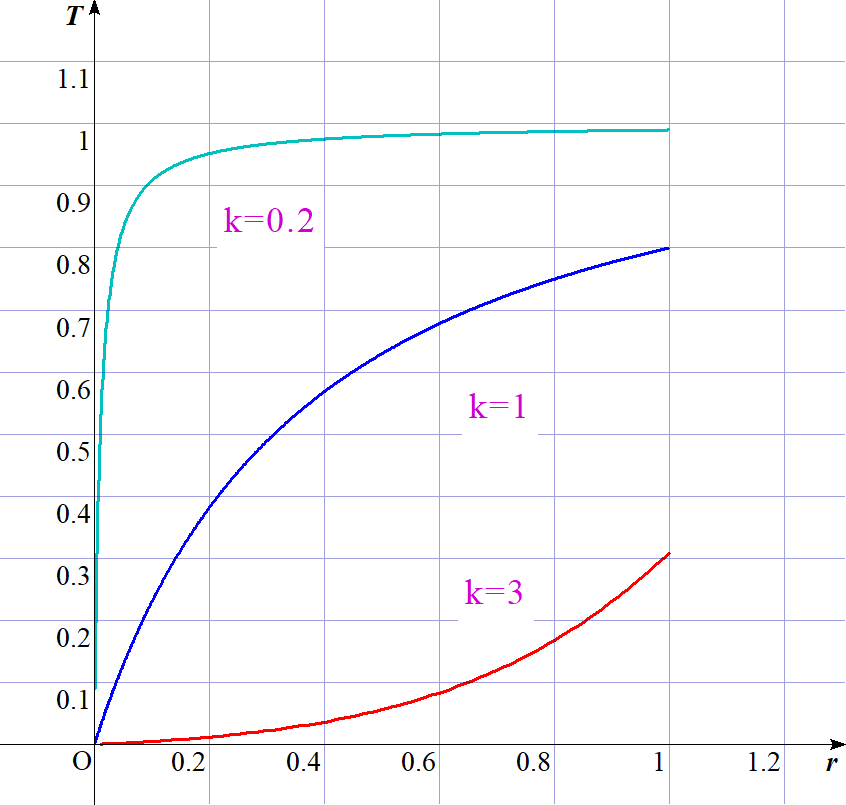
$ここで、k=a \sqrt{\cfrac{2mV_0}{\hbar ^2}},\ \ r=\cfrac{E}{V_0}\ \ とおくと$
$T=\cfrac{1}{1+\cfrac{\sinh ^2 k \sqrt{1-r}}{4r(1-r)}}$
$kをパラメータ、rを変数としたグラフは右のとおりです。$
$領域Ⅱの幅aが小さいと、パラメータkの値は小さくなり、$
$\cfrac{V_0}{E}=0.5\ 程度でも透過率は0.6\ 以上になることがわかります。$
$つまり、かなり高い確率でポテンシャル障壁をすり抜けてし$
$まうわけです。$
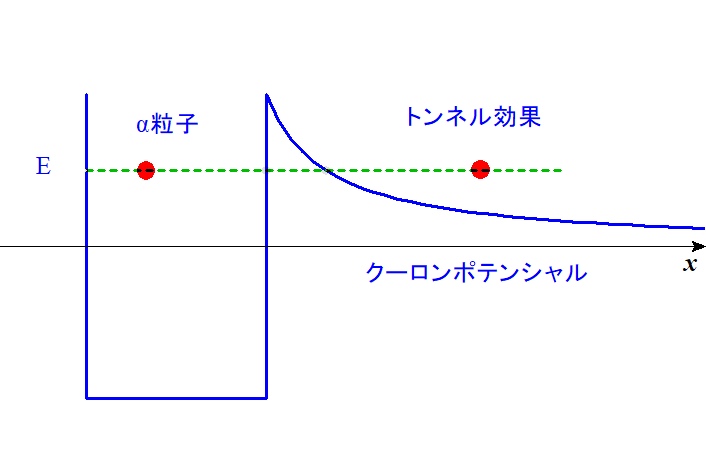
$トンネル効果の例$
$ウラン、トリウム、ラジウム等の原子核から\alpha線$
$(ヘリウムの原子核)が出てくる\alpha 崩壊という現象を$
$ロシアのガモフがこのトンネル効果を使って説明しました。$
$原子核内部では、強い力の核力が働いていますが、トンネル$
$効果により、\alpha粒子がこのエネルギー障壁を通り抜けて、$
$原子核から飛び出てくるわけです。$
$一度核外に飛び出た\alpha粒子は強い力の影響は受けず、また$
$クーロン力(電磁気力)は斥力であるので引き戻されることは$
$ありません。$
量子力学メニュー に戻る
メインメニュー に戻る