反射・透過
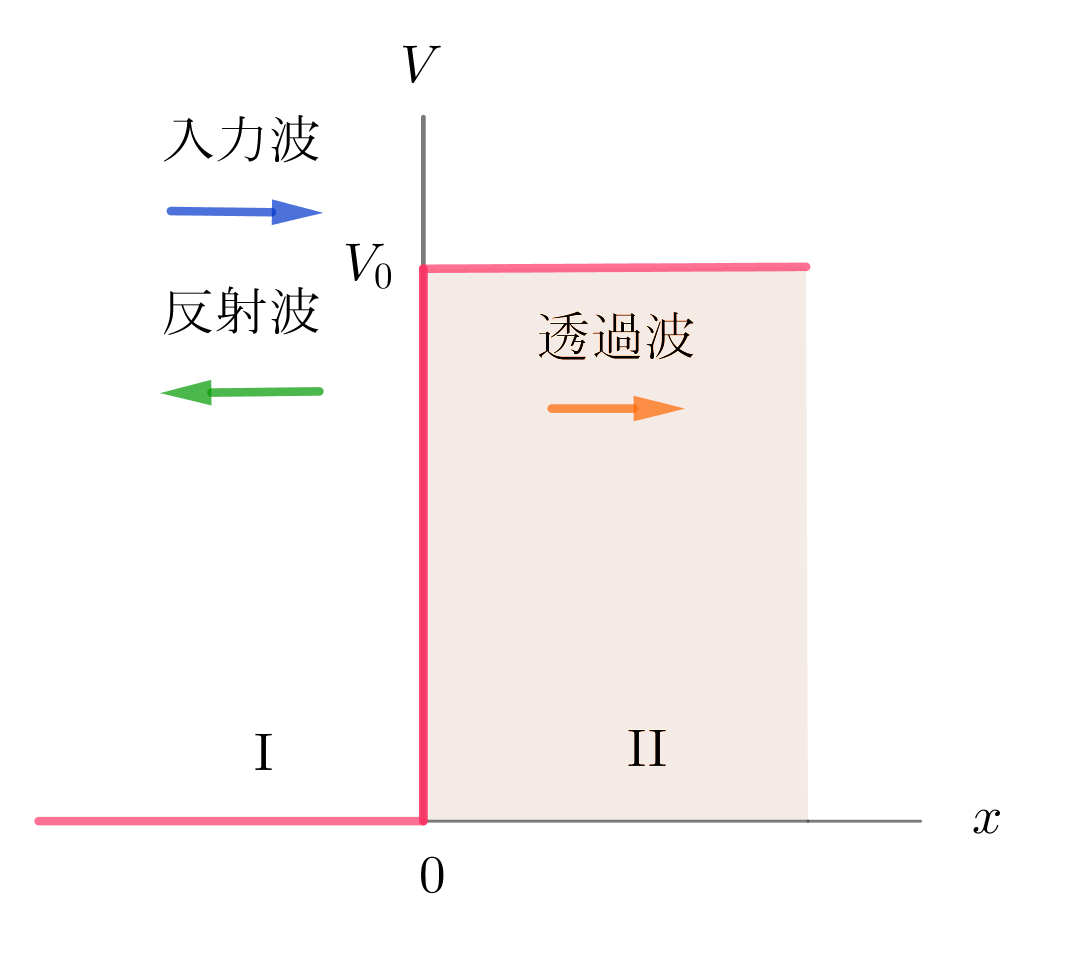
$右図は有限な高さの階段状のポテンシャルです。$
$V_0 > 0 \ として$
\[V(x)=
\left\{ \begin{array}{l}
0 \hspace{3em} (x < 0)\\
V_0 \hspace{3em} (x \geqq 0 )\\
\end{array} \right.
\]
$を考えます。$
$左から壁に向かって入射された、エネルギーE の量子は、$
$壁で反射される量子もあれば、壁を透過する量子もあります。$
$量子が、エネルギー障壁を超えることができるのか、透過するとはどういうことか、$
$いろいろ疑問はありますが、まずはシュレディンガー方程式を解いてみましょう。$
$(Ⅰ) \ \ E > V_0 のとき$
$(ア) \ 領域 \ Ⅰ \ では$
$\qquad -\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}\varphi(x)=E\varphi(x)\ \ より \cfrac{d^2 }{dx^2}\varphi(x)=-\cfrac{2mE}{\hbar ^2} \varphi(x)$
$\qquad \alpha=\cfrac{\sqrt{2mE}}{\hbar}\ \ とおくと \qquad \cfrac{d^2 }{dx^2}\varphi(x)=-\alpha ^2 \varphi(x)$
$\quad 入射波と反射波が存在するから$
$\qquad \varphi_1(x)=Ae^{i\alpha x}+Be^{-i\alpha x}$
$(イ) \ 領域Ⅱでは$
$\qquad -\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}\varphi(x)+V_0\varphi(x)=E\varphi(x) \ \ より \cfrac{d^2 }{dx^2}\varphi(x)=-\cfrac{2m(E-V_0)}{\hbar ^2} \varphi(x)$
$\qquad \beta=\cfrac{\sqrt{2m(E-V_0)}}{\hbar} \ \ とおくと \qquad \cfrac{d^2 }{dx^2}\varphi(x)=-\beta ^2 \varphi(x)$
$\qquad \varphi_2(x)=Ce^{i \beta x}+De^{-i \beta x}$
$領域Ⅱでは、右方向に向かう波だけだから \ D=0 \ となります。$
$これらの接続条件は$
$\quad \varphi_1(0)=\varphi_2(0)\ \ より A+B=C $
$\quad \varphi_1'(0)=\varphi_2'(0)\ \ より Ai\alpha -Bi\alpha =Ci\beta $
$Cを消去すると$
$\qquad A(\alpha -\beta)=B(\alpha +\beta)$
$\qquad \therefore \cfrac{B}{A}=\cfrac{\alpha - \beta}{\alpha +\beta}$
$確率の流れで示したとおり$ (確率の流れ参照)$確率は保存されるから、反射率は入射波の流れ密度と$
$反射波の流れ密度の比で定義されます。$
$\qquad 反射率=\cfrac{反射波のS}{入射波のS}=\cfrac{\cfrac{\hbar \alpha}{m}|B|^2}{\cfrac{\hbar \alpha}{m}|A|^2}=\cfrac{|B|^2}{|A|^2}=\left(\cfrac{\alpha - \beta}{\alpha +\beta}\right )^2
=\left(
\cfrac{\cfrac{\sqrt{2mE}}{\hbar }-\cfrac{\sqrt{2m(E-V_0)}}{\hbar }}
{\cfrac{\sqrt{2mE}}{\hbar }+\cfrac{\sqrt{2m(E-V_0)}}{\hbar }}
\right )^2
=\left(
\cfrac{\sqrt{E}-\sqrt{E-V_0}}{\sqrt{E}+\sqrt{E-V_0}}
\right )^2$
$反射率をR,\ \ r=\cfrac{E}{V_0} \ \ とおくと$
$\qquad R=\left(\cfrac{\sqrt{r}-\sqrt{r-1}}{\sqrt{r}+\sqrt{r-1}}\right )^2$
$また、Bを消去すると$
$\qquad 2A\alpha=C(\alpha +\beta)$
$\qquad \cfrac{C}{A}=\cfrac{2\alpha }{\alpha +\beta}$
$透過率も反射率同様に、入射波の流れ密度と透過波の流れ密度の比で定義されます。$
$\qquad 透過率=\cfrac{透過波のS}{入射波のS}=\cfrac{\cfrac{\hbar \beta}{m}|C|^2}{\cfrac{\hbar \alpha}{m}|A|^2}=\cfrac{\beta |C|^2}{\alpha |A|^2}=\cfrac{\beta}{\alpha}\left(\cfrac{2 \alpha }{\alpha +\beta}\right )^2=\cfrac{4\alpha \beta}{(\alpha + \beta)^2}
=\cfrac{4\cfrac{\sqrt{2mE}}{\hbar }\cfrac{\sqrt{2m(E-V_0)}}{\hbar }}
{\left(\cfrac{\sqrt{2mE}}{\hbar }+\cfrac{\sqrt{2m(E-V_0)}}{\hbar }\right )^2}$
$\hspace{5em}=\cfrac{4\sqrt{E}\sqrt{E-V_0}}{(\sqrt{E}+\sqrt{E-V_0})^2}$
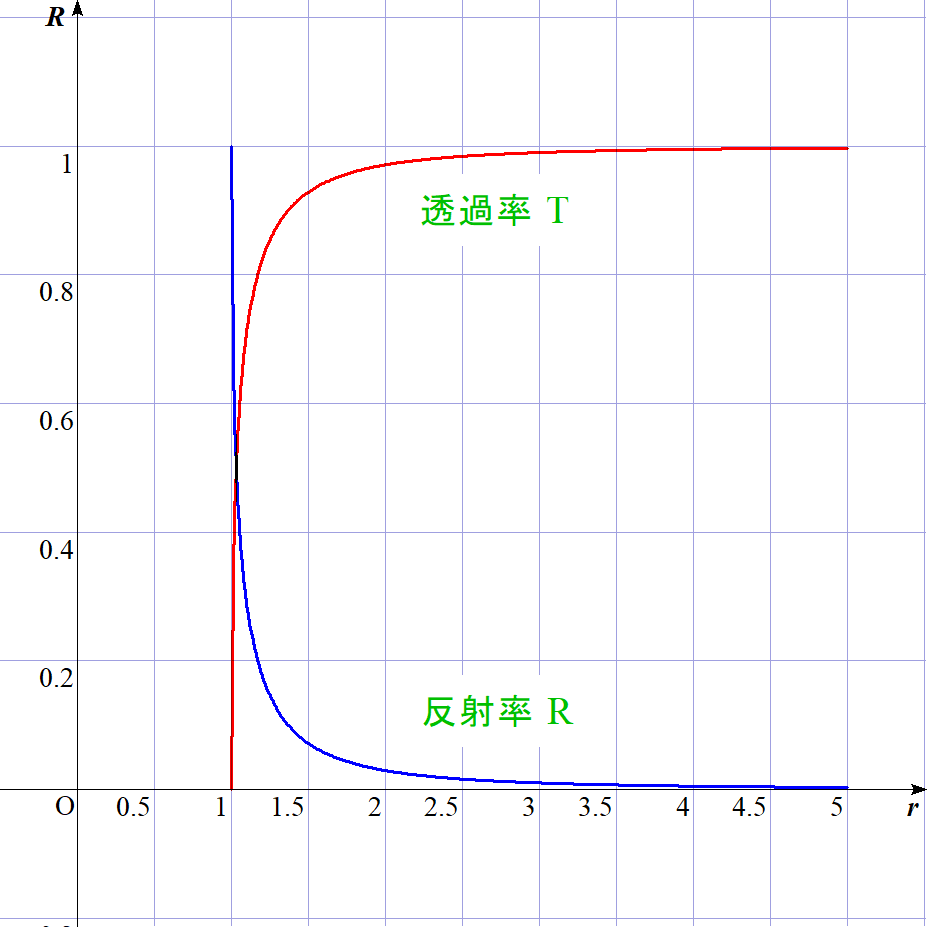
$透過率をT,\ \ r=\cfrac{E}{V_0} \ \ とおくと$
$\qquad T=\cfrac{4\sqrt{r}\sqrt{r-1}}{(\sqrt{r}+\sqrt{r-1})^2}$
$RとTのグラフは右図のとおりで、$
\begin{eqnarray*}
R+T
&=&\left(\cfrac{\alpha - \beta}{\alpha +\beta}\right )^2+\cfrac{4\alpha \beta}{(\alpha + \beta)^2}\\
\\
&=&\cfrac{(\alpha - \beta)^2+4\alpha \beta}{(\alpha + \beta)^2}\\
\\
&=&1\\
\end{eqnarray*}
$となって、確率が保存される意味がわかったような気になります。$
$(Ⅱ) \ \ E < V_0 \ \ のとき$
$(ア) \ 領域 \ Ⅰ \ では(Ⅰ)に同じです。$
$(イ) \ 領域 \ Ⅱ \ では$
$\qquad -\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}\varphi(x)+V_0\varphi(x)=E\varphi(x) \ \ より \cfrac{d^2 }{dx^2}\varphi(x)=\cfrac{2m(V_0-E)}{\hbar ^2} \varphi(x)$
$\qquad \gamma=\cfrac{\sqrt{2m(V_0-E)}}{\hbar} \ \ とおくと \qquad \cfrac{d^2 }{dx^2}\varphi(x)=\gamma ^2 \varphi(x)$
$\therefore \qquad \varphi_3(x)=Ce^{\gamma x}+De^{- \gamma x}$
$x \longrightarrow +\infty のとき \varphi_3が収束するためには \ C=0 \ でなければなりません。$
$よって \varphi_3=De^{-\gamma x}$
$これらの接続条件は$
$\quad \varphi_1(0)=\varphi_3(0)\ \ より A+B=D $
$\quad \varphi_1'(0)=\varphi_3'(0)\ \ より Ai\alpha -Bi\alpha =-\gamma D $
$Dを消去すると$
$\qquad A(i\alpha +\gamma)-B(i\alpha -\gamma)=0$
$\qquad \cfrac{B}{A}=\cfrac{i\alpha + \gamma}{i\alpha -\gamma}$
$\qquad |\cfrac{B}{A}|^2=\cfrac{\alpha ^2+ \gamma ^2}{\alpha ^2 +\gamma ^2}=1$
$したがって、反射率 \ R=1 \ となり、透過率 \ T=0 \ となります。$
$このとき、\varphi_3=De^{-\gamma x} は実数だから \ S=0 \ となって、確率の流れは \ 0 \ です。$
$これは、T=0 \ だから当然です。とはいえ、\varphi_3=0 \ ではありませんので、領域 \ Ⅱ \ に侵入する$
$量子もあるのですが、結局は引き戻されてしまうからです。$
量子力学メニュー に戻る
メインメニュー に戻る