MY MATH NOTE

球対称な無限に深い井戸型ポテンシャル

　
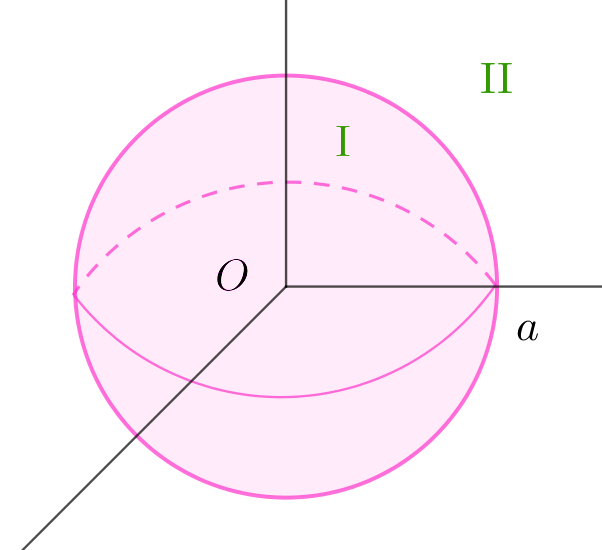
$右図のように、粒子が半径aの球内の領域に完全に$
$閉じ込められている状態のポテンシャルは、$

\[V(r)= \left\{ \begin{array}{l} 0 \hspace{3em} (0 \leqq r \leqq a )　\hspace{3em}領域 \ Ⅰ\\ \infty \hspace{3em} (r > a) \hspace{5em} 領域 \ Ⅱ\\ \end{array} \right. \] $粒子は領域 \ Ⅱでは存在できません。$
$加えて、波動関数もs波とよばれる角度に$
$よらない球対称な波とします。$

$領域 \ Ⅰでのシュレディンガー方程式は$
$動径方向について\ \ u=rR(r)\ \ とおくと$

$\qquad -\cfrac{\hbar ^2}{2m} \cfrac{d^2}{dr^2}u(r) =Eu(r) \hspace{19em}(1)$

$\quad k^2=\cfrac{2m}{\hbar ^2}E \ \ とおくと \quad (1)は \qquad \cfrac{d^2 }{dr^2}u(r)=-k^2u(r) \hspace{7em}(2)$

$解は　\quad u(r)=A\cos kr+B\sin kr $
$境界条件より$
$\quad u(0)=0 \times R(0)=0 \ \ だから　A=0$
$\quad u(a)=a \times R(a)=0 \ \ だから　B\sin ka=0 $
$\therefore k=\cfrac{n \pi}{a} \quad (n=1,2,3,\cdots )$
$あらためて u(r) を u_n(r) \ \ とおくと$
\begin{eqnarray*} u_n(r)&=&B\sin kr\\ &=&B\sin \cfrac{n\pi}{a}r \quad (n=1,2,3,\cdots )\\ \end{eqnarray*}

　
$したがって、波動関数は$
$\quad \psi(r,\theta,\varphi)=YR_n(r) ＝\cfrac{BY}{r}\sin \cfrac{n\pi}{a}r$

$Yの意味については$ (球対称なポテンシャルのシュレディンガー方程式を参考にしてください)

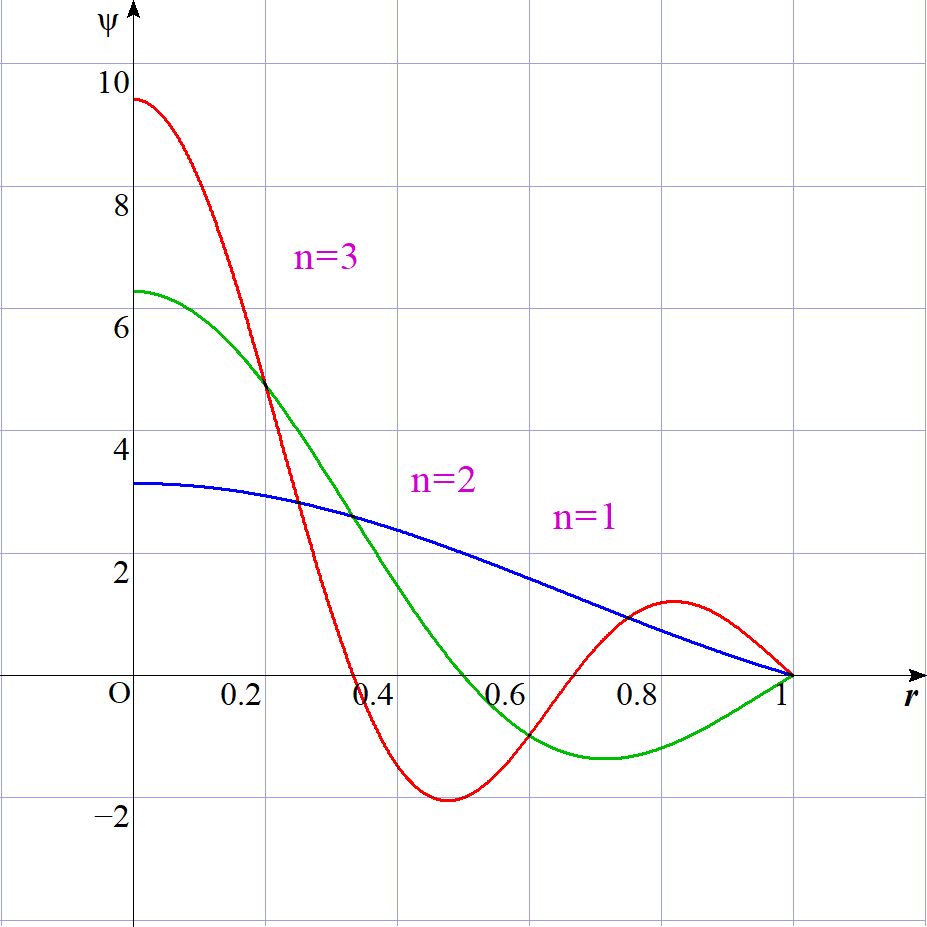
$a=1,\ BY=1 \ とした、n=1,2,3 の場合の$
$\psi(r,\theta,\varphi)\ \ のグラフは右のとおりです。$

$とくに$
$\quad r \rightarrow 0 \ \ のとき \ \ \psi \rightarrow \ n\pi \ \ です。$


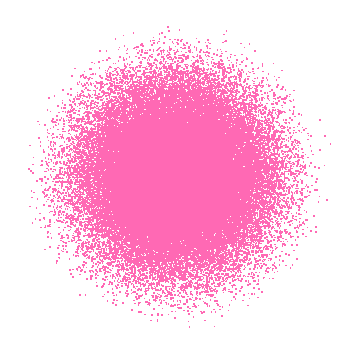
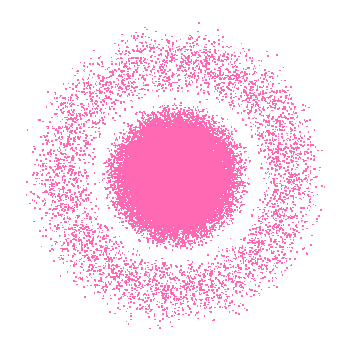
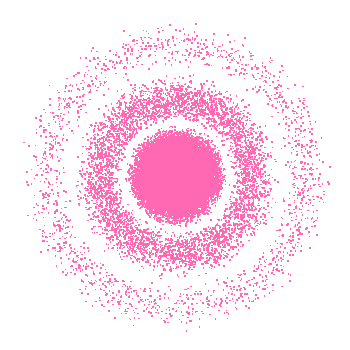
$粒子がこの波動関数に従うときの存在確率をドットで表現し、n=1,\ 2,\ 3 \ \ について$
$シミュレーションした結果が下図です。3次元空間をxy平面に射影したものです。$
$Visual \ Basic をつかって、10万個の点を表示しました。$

$n=2,\ 3\ で \ \psi=0 \ となるrのあたりでは、見いだされる確率は小さいので、白いリングに$
$なっているのがわかります。$

$\hspace{3em}$

$\hspace{2em}$

$\hspace{2em}$

ページの先頭へ↑