球対称なポテンシャルのシュレディンガー方程式
1 球面座標によるシュレディンガー方程式
$粒子間に働く力が2点間の距離rのみによるとき、$
$これを中心力といいます。$
$このとき、ポテンシャルは角度要素がありませ$
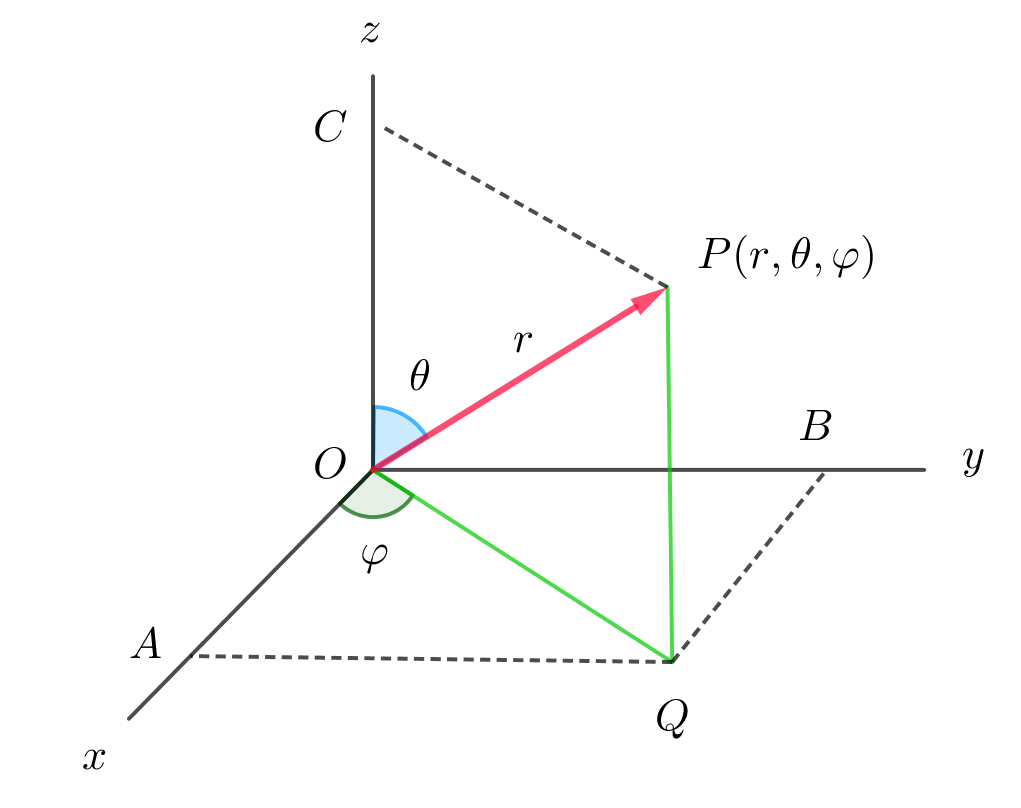
$んから球対称となり、xyz直交座標系よりも、$
$右図のような球面座標系(空間極座標系ともいい$
$ます)の方が扱いが楽になります。$
$両座標系の変換式は$
\[
\left\{ \begin{array}{l}
x=r\sin \theta \cos \varphi \\
y=r\sin \theta \sin \varphi \\
z=r\cos \theta \\
\end{array} \right.
\]
$ただし r >0 ,\ \ 0 \leqq \theta \leqq \pi , \ \ 0 \leqq \varphi < 2\pi $
$空間における、時間に依存しないシュレディンガー方程式のxyz直交座標表示は$
$\qquad -\cfrac{\hbar ^2}{2m}\big(\cfrac{\partial^2 \psi}{\partial x^2}+ \cfrac{\partial^2 \psi}{\partial y^2}+\cfrac{\partial^2 \psi}{\partial z^2}\big)+V \psi =E\psi$
$ですが、ラプラシアン \ \ \nabla ^2 =\cfrac{\partial^2 }{\partial x^2}+ \cfrac{\partial^2 }{\partial y^2}+\cfrac{\partial^2 }{\partial z^2}\ \ を球面座標に書き直す必要があります。$
$球面座標によるラプラシアンは$
$\hspace{4em} \nabla ^2 \psi
=\cfrac{1}{r^2}\cfrac{\partial}{\partial r}\big(r^2\cfrac{\partial \psi}{\partial r}\big)
+\cfrac{1}{r^2\sin \theta }\cfrac{\partial}{\partial \theta }\big(\sin \theta \cfrac{\partial \psi}{\partial \theta}\big)
+\cfrac{1}{r^2\sin ^2 \theta }\cfrac{\partial ^2 \psi}{\partial \varphi ^2}$
$でしたので、$ (球面座標のラプラシアンを参考にしてください)
$シュレディンガー方程式は$
$\qquad -\cfrac{\hbar ^2}{2m}\left\{\cfrac{1}{r^2}\cfrac{\partial}{\partial r}\big(r^2\cfrac{\partial \psi}{\partial r}\big)
+\cfrac{1}{r^2\sin \theta }\cfrac{\partial}{\partial \theta }\big(\sin \theta \cfrac{\partial \psi}{\partial \theta}\big)
+\cfrac{1}{r^2\sin ^2 \theta }\cfrac{\partial ^2 \psi}{\partial \varphi ^2}\right\}
+V\psi=E\psi$
2 球対称なポテンシャルのシュレディンガー方程式
$ポテンシャルを球対称とし、加えて波動関数もs波とよばれる球対称な波とします。$
$球対称ということから、ポテンシャルはV(x,y,z)=V(r),\ 波動関数\psi(x,y,z)は動径部分を$
$R(r),角度部分Y(\theta,\varphi)は定数Yとおけるから、\psi(r,\theta,\varphi)=YR(r) \ \ とおきます。$
$\quad \cfrac{\partial \psi}{\partial \theta }=0,\quad \cfrac{\partial ^2 \psi}{\partial \varphi ^2}=0 \ \ だから$
$\quad -\cfrac{\hbar ^2}{2m}\left \{\cfrac{1}{r^2}\cfrac{\partial}{\partial r}\big(r^2 Y \cfrac{d}{dr}R(r)\right\}+V(r)YR(r)=EYR(r)$
$\quad -\cfrac{\hbar ^2}{2m}\cfrac{Y}{r^2}\left\{2r\cfrac{d}{dr}R(r)+r^2\cfrac{d^2}{dr^2}R(r)\right\}+V(r)YR(r)=EYR(r)$
$\quad -\cfrac{\hbar ^2}{2m}\big(\cfrac{d^2}{dr^2}+\cfrac{2}{r}\cfrac{d}{dr}\big)R(r)+V(r)R(r)=ER(r)$
$これを動径方向のシュレディンガー方程式といいます。$
$この微分方程式を解くには、R(r)=\cfrac{u(r)}{r} \ \ と変換します。$
$\hspace{2em} \cfrac{d}{dr}R(r)=-\cfrac{1}{r^2}u+\cfrac{1}{r}u'$
\begin{eqnarray*} \cfrac{d^2}{dr^2}R(r) &=&\cfrac{2}{r^3}u-\cfrac{1}{r^2}u'-\cfrac{1}{r^2}u'+\cfrac{1}{r}u''\\ &=&\cfrac{1}{r}u''-\cfrac{2}{r^2}u'+\cfrac{2}{r^3}u\\ \end{eqnarray*} $よって$
$\qquad \big(\cfrac{d^2}{dr^2}+\cfrac{2}{r}\cfrac{d}{dr}\big)R(r)=\big(\cfrac{1}{r}u''-\cfrac{2}{r^2}u'+\cfrac{2}{r^3}u\big)+\cfrac{2}{r}\big(-\cfrac{1}{r^2}u+\cfrac{1}{r}u'\big)=\cfrac{1}{r}u''$
$シュレディンガー方程式は$
$\qquad -\cfrac{\hbar ^2}{2m}\cfrac{1}{r}\cfrac{d^2u}{dr^2}+V(r)\cfrac{u}{r}=E\cfrac{u}{r}$
$\qquad -\cfrac{\hbar ^2}{2m}\cfrac{d^2u}{dr^2}+V(r)u=Eu$
$これは、uについての1次元のシュレディンガー方程式そのものですから、扱いが簡単になります。$
量子力学メニュー に戻る
メインメニュー に戻る