有限な深さの井戸型ポテンシャル
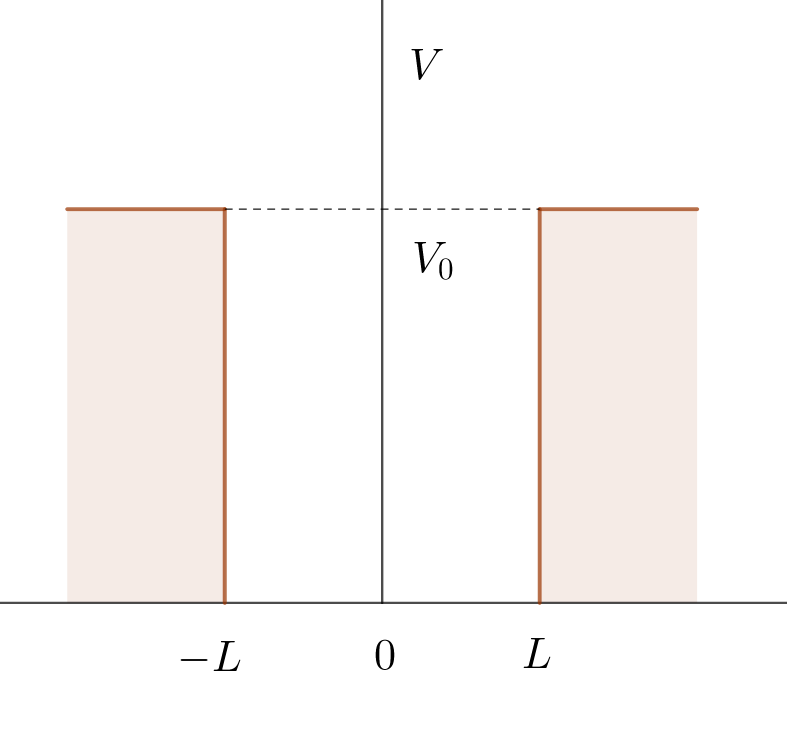
$シュレディンガー方程式の例題2は有限な深さの井戸型$
$ポテンシャルです。$
$V_0 > 0 \ として右図のようなポテンシャル$
\[V(x)=
\left\{ \begin{array}{l}
V_0 \hspace{3em} (x < -L,x > L)\\
0 \hspace{3em} (-L \leqq x \leqq L )\\
\end{array} \right.
\]
$を考えます。$
$このポテンシャルは V軸について対称、$
$すなわち V(-x)=V(x) を満たす偶関数です。$
$E < V_0 のとき、すなわちこのポテンシャル内を1次元運動する量子のシュレディンガー方程式は$
$\qquad \big(-\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}+V(x)\big)\varphi(x)=E\varphi(x) $
$x \rightarrow -x と置き換えると$
$\qquad \big(-\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}+V(-x)\big)\varphi(-x)=E\varphi(-x) $
$\therefore \qquad \big(-\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}+V(x)\big)\varphi(-x)=E\varphi(-x) $
$これは、\varphi(x) が解ならば \varphi(-x)も解であることを示しています。$
$束縛状態にある量子の、あるエネルギー固有値に対応する波動関数は、1次元シュレディンガー$
$方程式では1つしかないので$ (量子力学の基礎参照)
$\qquad \varphi(-x)=k\varphi(x) \quad (kは実数)とおけます。もう一度 x \rightarrow -x \ \ と置き換えると$
$\qquad \varphi(x)=k\varphi(-x)=k^2\varphi(x)$
$したがって \quad k^2=1 \qquad \therefore k=\pm 1$
(i)$\ \ k=1 のとき \varphi(-x)=\varphi(x) \ \ となって \varphi(x) は偶関数$
(ii)$\ \ k=-1 のとき \varphi(-x)=-\varphi(x) \ \ となって \varphi(x) は奇関数$
$となりますが、この\varphi(x)の偶奇性をパリティといいます。$
$以上のことから \ \ x \geqq 0 でシュレディンガー方程式を解けばよいことがわかりました。$
$(1)\ \ 0 \leqq x \leqq L \ \ のとき$
$\qquad -\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}\varphi(x) =E\varphi(x) $
$\qquad \alpha ^2=\cfrac{2m}{\hbar ^2}E \ \ とおくと \qquad \cfrac{d^2 }{dx^2}\varphi(x) =-\alpha ^2\varphi(x) $
$\quad よって解は \quad \varphi(x)=A\sin \alpha x+B\cos \alpha x $
$(2)\ \ x > L のとき$
$\qquad -\cfrac{\hbar ^2}{2m} \cfrac{d^2 }{dx^2}\varphi(x) +V_0\varphi(x)=E\varphi(x) $
$\qquad \cfrac{d^2 }{dx^2}\varphi(x) =\cfrac{2m(V_0-E)}{\hbar ^2}\varphi(x) $
$\qquad E < V_0 \ \ だから V_0 -E > 0 \qquad \beta ^2=\cfrac{2m(V_0-E)}{\hbar ^2} \ \ とおくと$
$\qquad \cfrac{d^2 }{dx^2}\varphi(x) =\beta ^2\varphi(x) $
$\quad 解は \quad \varphi(x)=Ce^{-\beta x} + De^{\beta x}$
$境界条件は \quad x \rightarrow +\infty \ \ のとき \varphi8x) \rightarrow 0 \ \ より D=0$
$したがって \quad \varphi(x)=Ce^{-\beta x}$
$(Ⅰ)\ \ パリティ偶の解$
\[\varphi(x)=
\left\{ \begin{array}{l}
B\cos \alpha x \hspace{2em} (0 \leqq x \leqq L)\\
Ce^{-\beta x} \hspace{3em} (x \geqq L)\\
\end{array} \right.
\qquad より \quad
\varphi '(x)=
\left\{ \begin{array}{l}
-\alpha B\sin \alpha x \hspace{2em} (0 \leqq x \leqq L)\\
-\beta C e^{-\beta x} \hspace{3em} (x \geqq L)\\
\end{array} \right.
\]
$x=Lでの接続条件は$
\[
\left\{ \begin{array}{l}
B\cos \alpha L=Ce^{-\beta L} \\
-\alpha B\sin \alpha L=-\beta Ce^{-\beta L}\\
\end{array} \right.
\]
$辺々割って$
$\qquad \cfrac{\alpha B\sin \alpha L}{B\cos \alpha L}=\cfrac{\beta Ce^{-\beta L}}{Ce^{-\beta L}} $
$\qquad \alpha \tan \alpha L=\beta$
$\qquad 両辺にLをかけて \quad \beta L=\alpha L\tan \alpha L$
$\qquad \eta=\beta L , \quad \xi=\alpha L \ \ とおくと \quad \eta = \xi \tan \xi$
$ただし$
\begin{eqnarray*}
\xi ^2+\eta ^2&=&\alpha ^2 L^2+\beta ^2 L^2\\
&=&\cfrac{2m}{\hbar ^2}E L^2 + \cfrac{2m(V_0-E)}{\hbar ^2} L^2\\
&=&\cfrac{2m}{\hbar ^2}V_0 L^2\\
\end{eqnarray*}
$したがって 点(\xi,\eta )は原点中心、半径 \cfrac{\sqrt{2mV_0}}{\hbar}L \ \ の円をえがく。$
$(Ⅱ)\ \ パリティ奇の解$
\[\varphi(x)=
\left\{ \begin{array}{l}
A\sin \alpha x \hspace{2em} (0 \leqq x \leqq L)\\
Ce^{-\beta x} \hspace{3em} (x \geqq L)\\
\end{array} \right.
\qquad より \quad
\varphi '(x)=
\left\{ \begin{array}{l}
\alpha A\cos \alpha x \hspace{3em} (0 \leqq x \leqq L)\\
-\beta C e^{-\beta x} \hspace{3em} (x \geqq L)\\
\end{array} \right.
\]
$x=Lでの接続条件は$
\[
\left\{ \begin{array}{l}
A\sin \alpha L=Ce^{-\beta L} \\
\alpha A\cos \alpha L=-\beta Ce^{-\beta L} \\
\end{array} \right.
\]
$辺々割って$
$\cfrac{\alpha A\cos \alpha L}{A\sin \alpha L}=\cfrac{-\beta Ce^{-\beta L}}{Ce^{-\beta L}} $
$\alpha \cot \alpha L=-\beta$
$両辺に L をかけて \quad \beta L=-\alpha L\cot \alpha L$
$\eta=\beta L , \quad \xi=\alpha L \ \ とおくと \quad \eta = -\xi \cot \xi$
$ただし \quad \xi ^2+\eta ^2 = \cfrac{2m}{\hbar ^2}V_0 L^2$
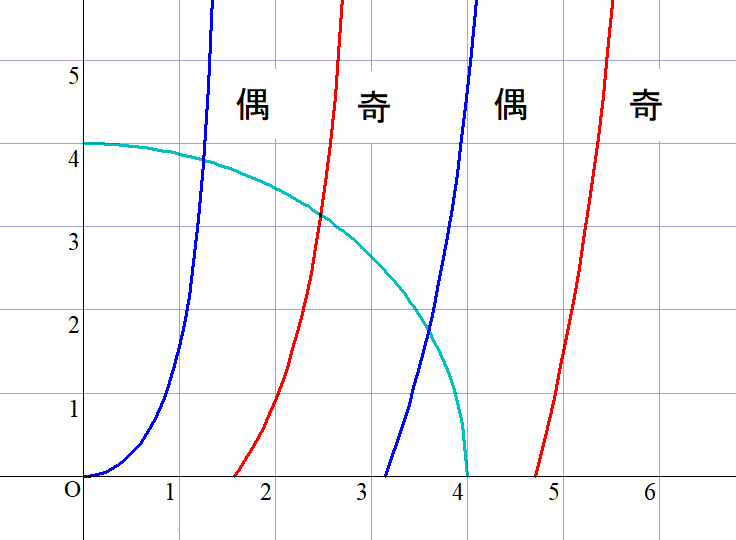
$(Ⅰ),(Ⅱ)の点(\xi,\eta)のグラフは右図のとおりで、原点中心、半径 \cfrac{\sqrt{2mV_0}}{\hbar }Lの円と交わる。$
$交点は、V_0L^2の値が小さいときは、偶関数との交点P_1(\xi_1,\eta_1)の１つであるが、$
$大きくなるにつれて、奇関数と偶関数に交互に点P_2(\xi_2,\eta_2),P_3(\xi_3,\eta_3),\cdots \ \ で交わる。$
$また、漸近線から、0 < \xi_1 < \cfrac{\pi}{2},\quad \cfrac{\pi}{2} < \xi_2 < \pi, \quad \pi < \xi_3 < \cfrac{3\pi}{2} \ \ であることがわかります。$
$L=\cfrac{\xi}{\alpha} \ \ に注意して、波動関数の変わり目の\ x=L\ の位置を調べてみましょう。$
$\xi=\xi_1,\ \ \xi_2,\ \ \xi_3 \ \ のときの波動関数を順に\ \ \varphi_1(x),\ \varphi_2(x),\ \varphi_3(x)\ \ とおくと$
$\varphi_1(x) \ \ については \quad 0 < \xi_1 < \cfrac{\pi}{2}\ \ より \ \ 0 < L < \cfrac{\pi}{2\alpha } \ \ で \ \ \varphi_1(\cfrac{\pi}{2\alpha})=B\cos (\alpha \times \cfrac{\pi}{2\alpha})=0$
$\varphi_2(x) \ \ については \quad \cfrac{\pi}{2} < \xi_2 < \pi \ \ より \ \ \cfrac{\pi}{2\alpha} < L < \cfrac{\pi}{\alpha } \ \ で \ \ \varphi_2(\cfrac{\pi}{\alpha})=A\sin (\alpha \times \cfrac{\pi}{\alpha})=0$
$\varphi_3(x) \ \ については \quad \pi < \xi_3 < \cfrac{3\pi}{2}\ \ より \ \ \cfrac{\pi}{\alpha} < L < \cfrac{3\pi}{2\alpha } \ \ で \ \ \varphi_3(\cfrac{3\pi}{2\alpha})=B\cos (\alpha \times \cfrac{3\pi}{2\alpha})=0$
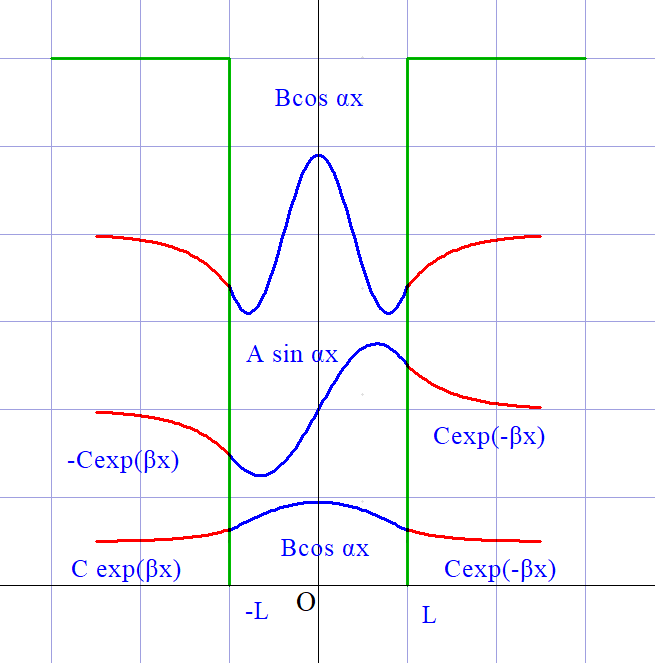$E=\cfrac{\hbar ^2}{2m}\alpha ^2=\cfrac{\hbar ^2}{2mL^2}\xi ^2 \ \ だから エネルギー$
$準位Eは離散的で、交点の\xi 座標の2乗に比例して$
$大きくなることがわかりますので、波動関数の$
$様子をエネルギー準位ごとに並べると右図のとおり$
$です。$
$ただし、\alpha ^2=\cfrac{2m}{\hbar ^2}E \ \ ですからEが変われば\alpha も$
$変わりますが、グラフでは同じ\alpha を用いています。$
$このグラフからわかるように、x < -L,\quad x > L の$
$領域でも波動関数が伸びていることがわかります。$
$すなわち、量子の存在確率は完全に0ではないのです。$
$ここがニュートン力学と大きく異なる点です。$
量子力学メニュー に戻る
メインメニュー に戻る