2次体の整数



$\hspace{7em}項目1-5は別ファイルを読み込みます$



6　素数


$整数 \ \alpha の約数で、同伴数でない数を真の約数といいます。$
$\alpha が真の約数をもたないとき、素数といいます。$
$次の定理は、素数を判定する強力なものです。$

$\quad 定理(素数判定)\hspace{2em} 整数\alpha のノルムN(\alpha) の絶対値が素数ならば、\alpha は素数である。$


$(証明)$
$\hspace{2em}背理法で示します$
$\hspace{2em}\alpha が素数でない(合成数といいます)とすると、\alpha =\beta \ \gamma \ \ となる整数 \ \ \beta ,\ \ \gamma \ が存在する。$
$\hspace{2em}|N(\alpha)| =p \ とおくと仮定よりpは素数である。$

$\hspace{2em}|N(\beta)||N(\gamma)|=1 \times p \ より　|N(\beta)| \ \ または \ \ |N(\gamma)|\ は1となる。$

$|N(\beta)|=1\ \ ならば \ \ \beta は単数となり、\alpha は真の約数をもたない。$
$\hspace{2em}よって、\alpha は素数となり、素数でないことに矛盾する。$

$\hspace{2em}|N(\gamma)|=1\ \ のときも同様である。$


$例1\ \ ガウス整数で$

$\quad N(1+i)=(1+i)(1-i)=2 \ \ は素数だから、1+i \ は素数$

$例2\ \ ガウス整数で、2は素数か$

$\quad (1+i)(1-i)=2 \ \ となる整数\ 1+i,\ \ 1-i \ があるから 2は素数でない。!!$

$例3 \ \ ガウス整数で、3は素数か$

$素数でないとすると　3=\beta \ \gamma \ \ とおけるから$
$\quad N(3)=N(\beta)N(\gamma) \qquad \therefore N(\beta)N(\gamma)=9$
$ガウス整数では \ N(\beta)>1,\ \ N(\gamma)>1 \ \ だから \ \ N(\beta)=N(\gamma)=3$
$\quad N(\beta)=3 \ について　\beta =p+qi \ \ とおくと$
$\quad p^2+q^2=3 \ \ よって　(p^2,q^2)=(0,3),\ (1,2),\ (2,1),\ (3,0)$
$ところが、これを満たす有理整数p,q は存在しない。よって　3\ は素数$


　

ページの先頭へ↑





7　素因数分解


$例1$
$Q(\sqrt{2})において、N(2)=4 \ \ は有理素数でないから素数判定定理が使えない。$
$ところが、　(2+\sqrt{2})(2-\sqrt{2})=2 \ \ であり、N(2+\sqrt{2})=N(2-\sqrt{2})=2 \ \ は有理素数だから$
$\qquad 2+\sqrt{2}　と　2-\sqrt{2}　はともに素数である。$
$したがって、Q(\sqrt{2})で\ 2\ は素数でなく、2=(2+\sqrt{2})(2-\sqrt{2}) \ \ と素因数分解される。$


$例2$
$\quad Q(\sqrt{-5}) において、(2+\sqrt{-5})(2-\sqrt{-5})=9 \ \ だから$
$\quad 9=3^2=(2+\sqrt{-5})(2-\sqrt{-5})\ \ と因数分解される$

(i)$\ \ 3\ が\ Q(\sqrt{-5})\ で素数であること$

$\quad 3=\alpha \ \beta \ \ と素因数分解できたとすると、 N(3)=N(\alpha)N(\beta) \ \ より　 9=N(\alpha)N(\beta)$
$\quad N(\alpha) > 1, \ \ N(\beta)>1\ \ より \ \ N(\alpha)=3,\ \ N(\beta)=3$
$\quad \alpha =p+q\sqrt{-5} \ \ とおくと、N(\alpha)=p^2+5q^2=3$
$\quad これを満たす有理整数p,q はないから\ 3\ は素数である。$

(ii)$\ \ 2+\sqrt{-5}\ が素数であること$

$\quad 2+\sqrt{-5}=\gamma \ \delta \ \ と素因数分解できたとすると、 N(2+\sqrt{5})=N(\gamma)N(\delta)\ \ より \ \ 9=N(\gamma)N(\delta)$
$\quad N(\gamma) > 1,\ \ N(\delta)>1 \ \ より \ \ N(\gamma)=3,\ \ N(\delta)=3$
$\quad \delta =r+s\sqrt{-5} \ \ とおくと、N(\gamma)=r^2+5s^2=3$
$\quad これを満たす有理整数r,s はないから、2+\sqrt{-5}\ \ は素数である。$

$同様に、2-\sqrt{-5} が素数であることもいえる。$
$よって　(2+\sqrt{-5})(2-\sqrt{-5}) \ \ は素因数分解である。$

$すると$

$\qquad 9=3^2=(2+\sqrt{-5})(2-\sqrt{-5}) \quad と2通りに素因数分解されることになり$

$\qquad 素因数分解の一意性が成りたたない。!!$


$数十年前のことでしたが、それまで学んできた体は、すべて素因数分解が可能でしたので、$
$私にとって、非常な驚きとともに感動でした。$
$実は、これを伝えたくて、この原稿を書きました。$

$それでは、2次体において、素因数分解の一意性が成りたつのは、どういう場合でしょうか。$
$順を追って、詳しく見ていきましょう。$



　

ページの先頭へ↑




8　除法の原理


$a,bが自然数、あるいは有理整数のとき　a を b で割った商がq,余りがr であることは$
$\qquad a=b\ q+r \quad (ただし　0 \leqq r < b )$
$とかくことができます。$

$また、f(x),g(x)が整式(多項式ともいいます)のとき、f(x)をg(x)で割った商がq(x),$
$余りがr(x)であることは$
$\qquad f(x)=g(x)q(x)+r(x) \quad (ただし、r(x)の次数 < g(x) の次数)$
$とかくことができます。$

$このように表現できることを、除法の原理（整除可能）といいますが、今まで気にする$
$ことなく当たり前のようにやってきました。$

$2次体の整数についても、同じく除法の原理が成りたつかどうか調べてみましょう。$

$\quad 定義 \hspace{2em} 2次体\ \ Q(\sqrt{D}) の整数\ \alpha,\ \beta \ に対して$
$\hspace{6em} \alpha =\beta \ \kappa + \rho \quad (ただし　N(\rho) < N(\beta) )$
$\hspace{4em} を満たす整数 \ \kappa, \ \rho が存在するとき除法の原理が成りたつ（整除可能）という。$


$(1)\ \ Q(\sqrt{2})で考えてみましょう$

$\qquad \cfrac{\alpha}{\beta}=a+b\sqrt{2}\quad (a,b は有理数)\ \ とする。$

$有理数aに対して、aを超えない最大の有理整数を[a](ガウス記号)$
$で表すと$

　


(i)$\ \ a-[a] \leqq \cfrac{1}{2}\ \ のときは　g=[a]\ \ とすると \ \ a-g \leqq \cfrac{1}{2}$

　


(ii)$\ \ a-[a] > \cfrac{1}{2} \ \ のときは　g=[a]+1 \ \ とすると \ \ g-a \leqq \cfrac{1}{2}$

(i),(ii)$をまとめて$
$\qquad |a-g| \leqq \cfrac{1}{2}\ \ を満たす有理整数\ g\ がとれる。$

$同様にして、有理数bに対しても$
$\qquad |b-h| \leqq \cfrac{1}{2}\ \ を満たす有理整数\ h\ がとれる。$

$このg,\ h を用いて　\kappa =g+h\sqrt{2}\ \ をつくると　\kappa \ は整数となる。$
$したがって \qquad \rho =\alpha - \beta \ \kappa \ \ も整数となるから$
$\qquad \alpha =\beta \kappa + \rho \ \ と表せる。$

$また、ノルムについては$
$\qquad \cfrac{\alpha}{\beta}-\kappa=(a+b\sqrt{2})-(g+h\sqrt{2})=(a-g)+(b-h)\sqrt{2}\ \ だから$
\begin{eqnarray*} |N(\cfrac{\alpha}{\beta}-\kappa)|&=&|(a-g)^2-2(b-h)^2|\\ & \leqq &|a-g|^2+2|b-h|^2\\ & \leqq &\big(\cfrac{1}{2}\big)^2+2\big(\cfrac{1}{2}\big)^2\\ &=&\cfrac{3}{4}\\ & < &1\\ \end{eqnarray*} $\quad \rho =\alpha - \beta \ \kappa =\beta \big(\cfrac{\alpha}{\beta}-\kappa \big) \ \ より$
$\quad |N(\rho)| =|N(\beta)||N \big(\cfrac{\alpha}{\beta}-\kappa \big)| < |N(\beta)|$

$これで、Q(\sqrt{2}) が整除可能であることがわかりました。$

$証明のポイントは　|N(\cfrac{\alpha}{\beta}-\kappa)| <1 \ \ を示せたことです。$



$(2)\ \ ガウス整数で考えてみましょう。$

$例えば$

　

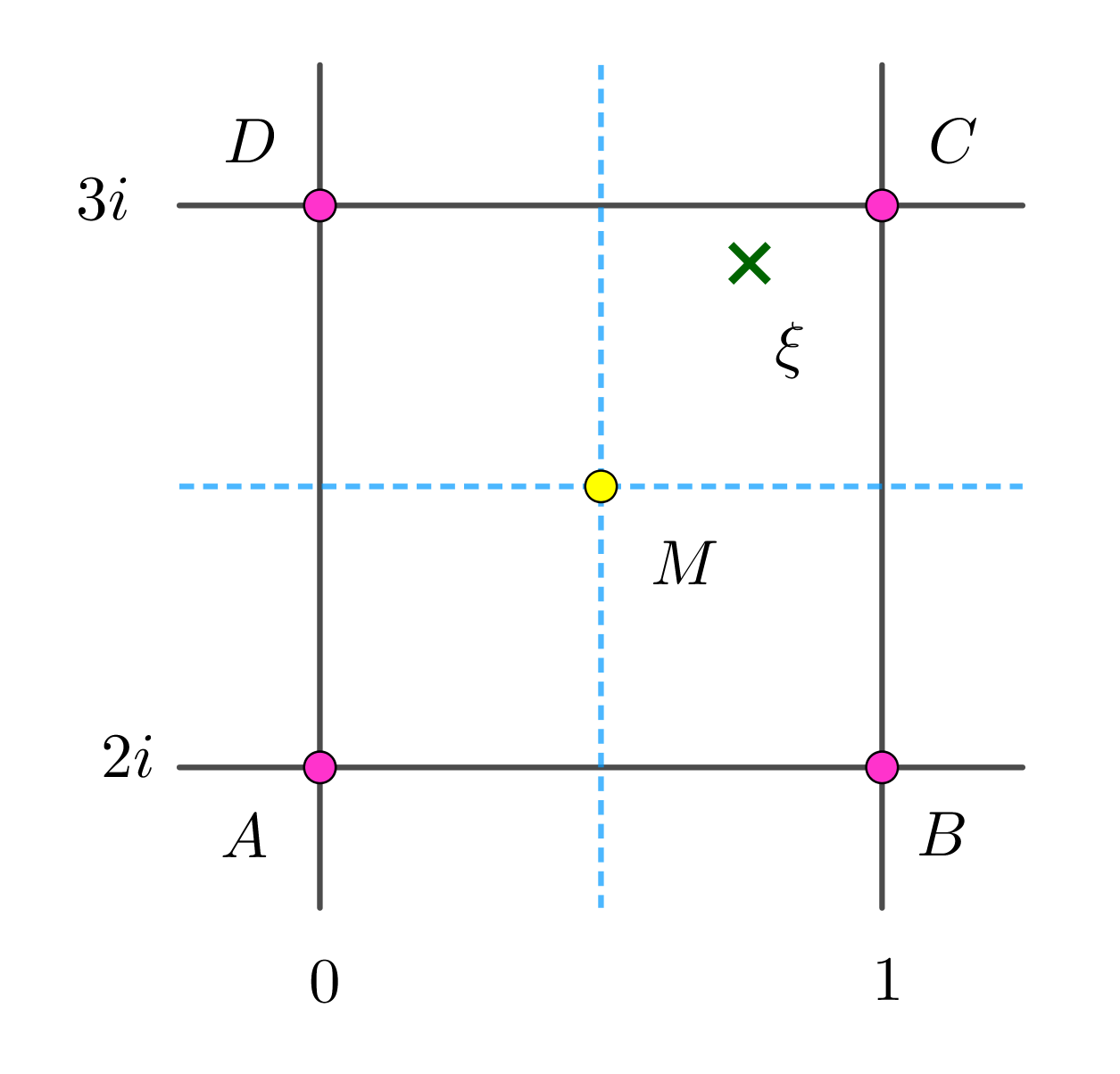
$\cfrac{7+4i}{2-2i}=\cfrac{(7+4i)(2+2i)}{(2-2i)(2+2i)}=\cfrac{3+11i}{4}=\cfrac{3}{4}+\cfrac{11}{4}i$

$ガウス平面上で、\xi=\cfrac{3}{4}+\cfrac{11}{4}i \ \ は点A(2i),\ B(1+2i),\ C(1+3i),$

$D(3i)\ \ を4頂点とする正方形の内部の点です。$
$この正方形をさらに、1辺 \ \cfrac{1}{2}\ の小正方形に4分割し、中心をMとします。$
$\xi \ は点Cを頂点とする小正方形の内部にあるから、\kappa =1+3i \ \ ととります。$
$すると$
$\quad 7+4i=(2-2i)(1+3i)-1$
$となって　商は　1+3i , \ \ 余りは　-1\ \ と求まります。$
$\quad N(2-2i)=8,\ \ N(-1)=1\ \ だから　除法の原理を満たしています。$

　

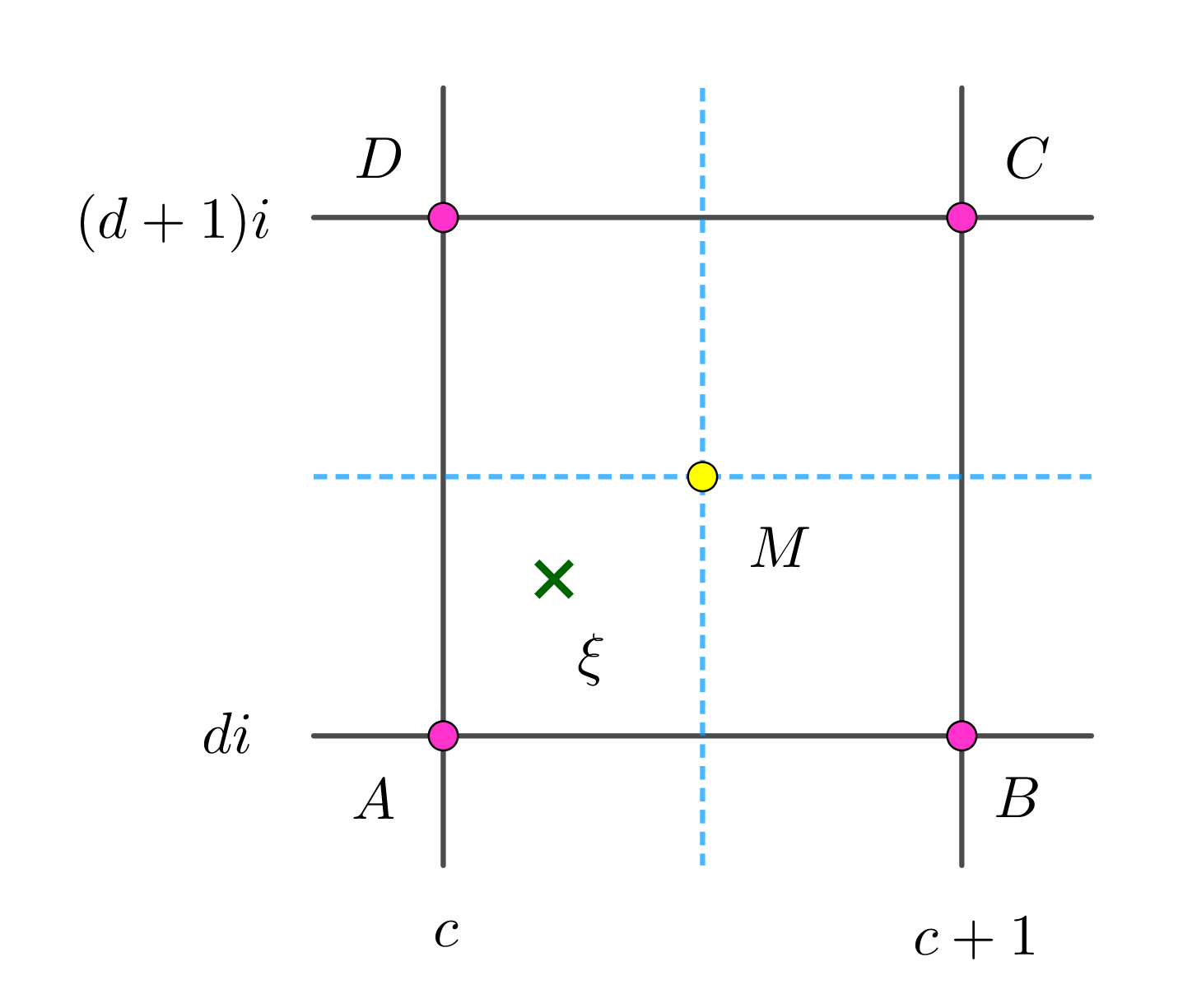
$一般に、\xi=\cfrac{\alpha}{\beta}=a+bi \quad (a,b は有理数) は$
$有理数aに対して、[a]=c,\ \ [b]=d \ \ とおくと$
$\xi は点A(c+di),B(c+1+di),C(c+1+(d+1)i),D(c+(d+1)i)を$
$4頂点とする正方形の内部または周上の点である。$

$この正方形をさらに、1辺\cfrac{1}{2}の小正方形に4分割し、$
$中心をMとする。$

$\xi はこれら4つの小正方形のどれかの内部に入るから、$
$入った小正方形の頂点A,B,C,Dの表す複素数を\kappa ととる。$

$例えば頂点Aのときは$
\begin{eqnarray*} |\xi - \kappa | & < & MA\\ & = & \cfrac{\sqrt{2}}{2}\\ & < & 1\\ \end{eqnarray*} $したがって、|N(\cfrac{\alpha}{\beta}-\kappa)| <1 \ \ が成りたつことが示せました。$

$これで、Q(\sqrt{-1}) が整除可能であることがわかりました。$


ページの先頭へ↑




9　整除可能性の判定


$一般に、除法の原理が成りたつかどうかを判定する方法について考えてみましょう。$

$2次体\ \ Q(\sqrt{D}) の整数\ \alpha,\ \beta \ に対して$
$\qquad \alpha =\beta \kappa + \rho \quad (ただし　N(\rho) < N(\beta) )$
$を満たす整数 \ \kappa, \ \rho が存在するとき整除可能といいいました。$

$\quad \rho =\alpha -\beta \kappa で　N(\rho) < N(\beta) \ \ だから$
$\quad |N(\alpha -\beta \kappa)| < |N(\beta)| $

$\quad |\cfrac{N(\alpha -\beta \kappa)}{N(\beta)}| < 1$

$\quad |N\big(\cfrac{\alpha -\beta \kappa}{\beta}\big)| < 1$

$\quad |N\big(\cfrac{\alpha}{\beta}- \kappa \big)| < 1$

$したがって、2次体の整数 \alpha ,\ \beta に対してこれを満たす整数 \ \kappa \ が存在すれば、除法の原理が$
$成りたつことになります。このような2次体を「ユークリッド2次体」といいます。$

$\quad ユークリッド2次体の判定定理$
$\hspace{4em} Q(\sqrt{D})の整数 \alpha ,\ \beta に対して \hspace{2em} |N\big(\cfrac{\alpha}{\beta}- \kappa \big)| < 1 $
$\hspace{4em} を満たす整数 \ \kappa \ \ が存在すればQ(\sqrt{D})はユークリッド2次体である。$



ページの先頭へ↑





10　素因数分解の一意性


$ユークリッド2次体において、整数\ \alpha を\ 整数\ \beta で割った商を\ \kappa \ 余りを\ \rho とすると$
$ 除法の原理　\alpha =\beta \kappa + \rho \quad (ただし　N(\rho) < N(\beta) ) \ \ が成りたちます。$
$引き続き　割る数 \beta を 余り\rho で割って商と余りを求め,この操作を繰返すと、最終的には$
$余り\rho \ \ が0になって割り切れます。$
$最後に割った数が\alpha と\beta の最大公約数となりますが、これをユークリッドの互除法といいます。$

$ユークリッドの互除法より、整数\alpha ,\ \beta \ が互いに素であれば、\alpha x+\beta y=1 \ \ を満たす$
$整数x,y が存在することが示せます。$

$これより、整数\alpha , \ \beta \ が互いに素で、\beta |\alpha \gamma \ \ (\beta \ は\alpha \ \gamma の約数)ならば　\beta|\gamma \ \ (\beta \ は\ \gamma \ の約数)がいえます。$

$これをつかって、素因数分解の一意性が導けますが、このあたりの説明はどの整数論の参考書に$
$ものっていますので、ここでは省略します。$

$この一連の流れからわかるように、$

$\hspace{2em} 除法の原理が成りたてば、ユークリッドの互除法が使え、素因数分解の一意性が導かれる。$


$素因数分解 の例2\ で見たように \ \quad 9=3^2=(2+\sqrt{-5})(2-\sqrt{-5})\ \ と2通りに素因数分解され、$
$一意性がなりたたないのは、9が素数3で割り切れるにもかかわらず、2+\sqrt{-5}\ も \ 2-\sqrt{-5}\ も$
$3で割り切れないからです。$
$実は、そもそもQ(\sqrt{-5}) では、|N(\cfrac{\alpha}{\beta}-\kappa)| <1 \ \ を満たす \kappa を見いだせないのです。$

$したがって、ユークリッド2次体であれば、素因数分解の一意性が成りたつことになりますが、$
$このときのDは,D < 0\ の虚2次体では5個、D > 0\ の実2次体で16個の有限個しかありません。$
$(説明はかなりやっかいです)$

$ところが、非ユークリッド2次体であっても、素因数分解が一意に決まる（これを単純体と$
$いいます)場合もあるのですが、これについてはイデアルがからんできますので、またの機会$
$にします。$



ページの先頭へ↑




メインメニュー　に戻る