アルキメデスの方法による円周率の計算


$(1)\ \ A_n と B_n の関係$

　

$半径１の円に内接する正$n$角形の一辺の長さをx_nとする。$

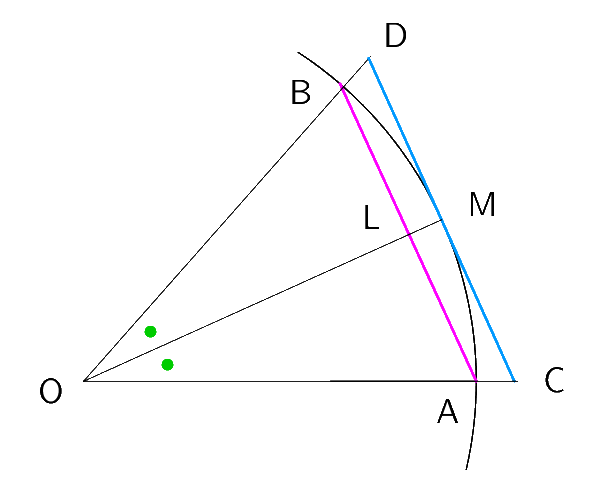
$A_n = n x_n,\quad OA=OM=1$
$AL=\cfrac{AB}{2}=\cfrac{x_n}{2},\quad CM=\cfrac{CD}{2}=\cfrac{B_n}{2n}$

$OL=\sqrt{OA^2-AL^2}=\sqrt{1-\cfrac{x_n^2}{4}}$
$△OAL \sim △OCM$　より $\cfrac{OL}{OM}=\cfrac{AL}{CM}$
$\hspace{2em} CM \times OL=OM \times AL$

$\hspace{2em} \cfrac{B_n}{2n} \times \sqrt{1-\cfrac{x_n^2 }{4}} = 1 \times \cfrac{x_n}{2}$

$\hspace{1em}\therefore B_n= \cfrac{n x_n}{\sqrt{1-\cfrac{x_n^2 }{4}}}=\cfrac{A_n}{\sqrt{1-\cfrac{x_n^2 }{4}}} \hspace{13em}$



(2) 内接する正n角形と正2n角形の辺の長さの関係

　

$\hspace{2em} 正n角形の頂点をA_k,A_{k+1}とし、$
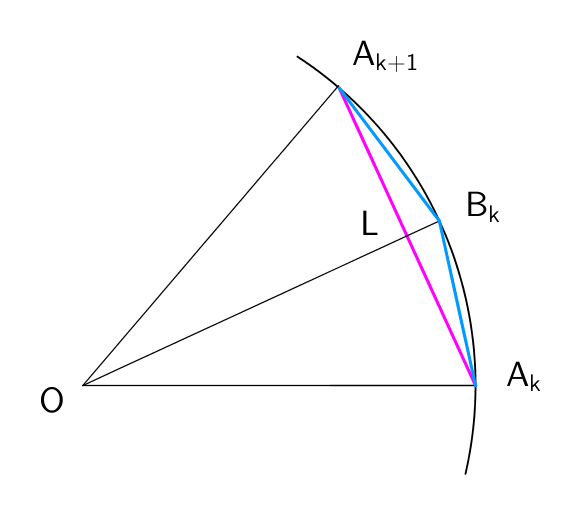
$\hspace{2em}$
$\hspace{2em} B_kは正2n角形の頂点であり、A_kB_kはその1辺となる。$

$\hspace{2em} A_kB_k^2=A_kL^2+B_kL^2 　だから$
$\hspace{2em} x_{2n} ^2=(\cfrac{x_n}{2})^2+(1-OL)^2$
$\hspace{4em} =\sqrt{\cfrac{x_n^2}{4}+\Bigl( 1-\sqrt{1-\cfrac{x_n^2}{4}} \Bigr) ^2} $


(3) 円周率の計算


(i)$\quad 正6角形から始めると$

$\hspace{2em} x_6=1 , \ A_6=6, \ B_6=\cfrac{6}{\sqrt{1-\cfrac{1^2}{4}}}=4\sqrt{3}$

　よって　 $3 < \pi < 2\sqrt{3}$

(ii)$\quad n=12 では$

$\hspace{2em} x_{12} = \sqrt{\cfrac{1^2}{4}+\Bigl( 1-\sqrt{1-\cfrac{1^2}{4}} \Bigr) ^2}=\sqrt{2-\sqrt{3}}
= \cfrac{\sqrt{3}-1}{\sqrt{2}}=\cfrac{\sqrt{6}-\sqrt{2}}{2}$

$\hspace{2em} A_{12}=12 \times \cfrac{\sqrt{6}-\sqrt{2}}{2}=6(\sqrt{6}-\sqrt{2})$
$\hspace{2em} B_{12}=\cfrac{A_{12}}{\sqrt{1-\cfrac{2-\sqrt{3}}{4}}}=\cfrac{12(\sqrt{6}-\sqrt{2})}{\sqrt{2+\sqrt{3}}} =\cfrac{12(\sqrt{6}-\sqrt{2})}{\cfrac{\sqrt{3}+1}{\sqrt{2}}}=24(2-\sqrt{3})$

　よって $\quad 3(\sqrt{6}-\sqrt{2}) < \pi < 12(2-\sqrt{3})$

$\therefore \quad 3.1058 < \pi < 3.2154$

$このように、正12角形まではどうにか計算できましたが、\pi を有理数で押さえることは$
$かなりの工夫がいるだろうと予想されます。$
$アルキメデスは正96角形まで考えたようですが、どうのようにして導いたのでしょうか。$

$これ以上の計算はコンピュータの力を借りることにします。結果は下表のとおりです。$

　


ページの先頭へ↑




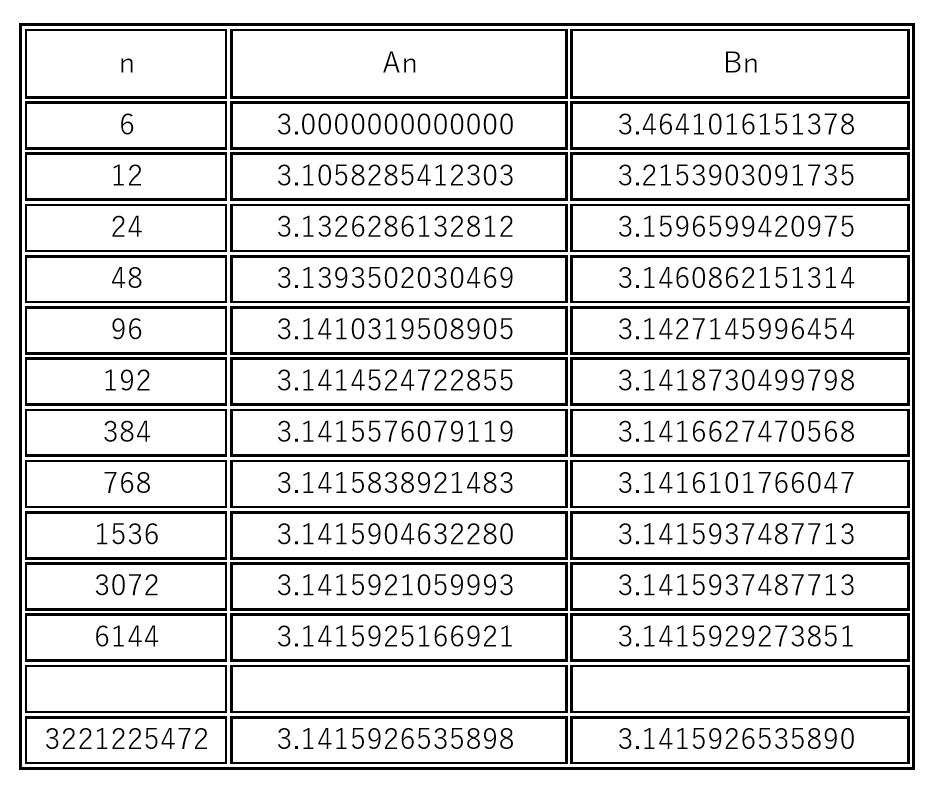
アルキメデスの方法　に戻る


メインメニュー　に戻る