円に内接・外接する正n角形


$\quad 定理 \quad 半径１の円に内接する正n角形の周をA_n、外接する正n角形の周をB_nとすると、$

$\hspace{5em}　A_n < 2\pi < B_n $


$この定理をきちんと証明しましょう。$

　

$(1)\ \ 円に内接・外接する正n角形$

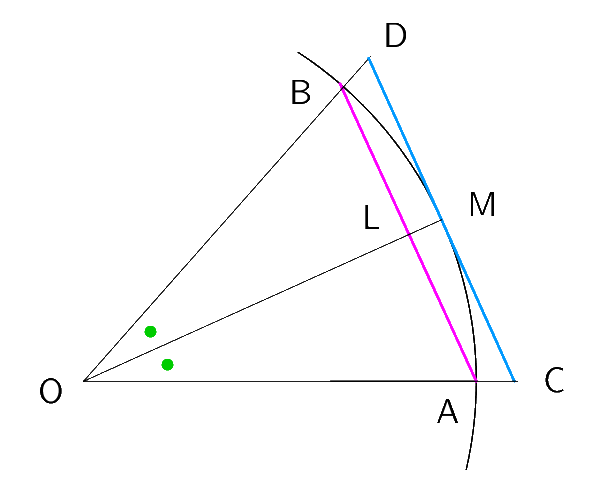
$円Oに内接する正n角形の1辺をABとし、∠AOB の二等分線$
$と線分ABとの交点をL,OLの延長と円Oとの交点をMとする。$

$点Mにおける円Oの接線と線分OA,OBの延長との交点を$
$それぞれC,Dとすると、△OCMと△ODMにおいて$
$\quad ∠COM =∠DOM$
$\quad 円の接線の性質より　CD \perp OM　だから　∠CMO=∠DMO$
$\quad OMは共通$
$1辺とその両端角が等しいので、△OCM \equiv △ODM$
$よって　OC=OD$

$∠CODは、内接正n角形の中心角だから、線分CDは円Oに外接する正n角形の1辺となる。$

$AB \perp OL \ \ だから \ \ AB \ // \ CD$


$(2)\ \ A_n < 2\pi 　の証明$

$２点を結ぶ最短曲線は直線であるから、内接正n角形の１つの辺ABと弧ABについて$
$\hspace{2em}$ 　
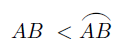
この関係がすべての辺について成りたつから、その和をとって

$\hspace{2em} A_n < 円Oの円周$

$\hspace{2em} \therefore A_n < 2\pi$


$(3)\ \ 2\pi < B_n$ 　の証明

この不等式は当然成り立つと思えるが、よくよく考えると難しい。

(i)$\ \ よく見かけるのは、扇形OMBの面積 < △OMDの面積　を使う方法である。$

$円は曲線で囲まれている図形であるから、その面積を求めるには極限の概念が必要である。$

$曲線 \ y=f(x)　(a \leqq x \leqq b) とx軸で囲まれた領域の面積は、区間 \ [a,b] \ をいくつかの$
$小区間に分割し、領域に含まれる細長い長方形の面積の和を考える。$
$分割を細かくしていったとき、この和の極限値が存在するならば、その値を面積と定義するが、$
$それを求める方法が定積分（リーマン積分）である。$

$半径rの円の面積が\ \pi r^2 \ であることはこのようにして求められるものである。$
$そのためには$
\[定積分　\longleftarrow 三角関数の微分法　 \longleftarrow 　 \lim_{\theta \to 0} \cfrac{sin \theta}{\theta}=1 \hspace{13em}\] $と遡らなくてはならない。$

$（小学校で習うように、円を多くの扇形に分割し、互い違いに並べて、長方形と見なす方法が$
$ありますが、扇形を二等辺三角形と見なすという極限が入っています。）$

$ところが、この極限値を高校の教科書では、扇形（円）の面積を用いて$
$\hspace{3em} \cfrac{1}{2}r^2\sin \theta<\cfrac{1}{2}r^2 \theta <\cfrac{1}{2}r^2\tan \theta $
$より$
\[\lim_{\theta \to 0} \cfrac{sin \theta}{\theta}=1 \hspace{22em}\] $を導いている。$
$すなわち、円の面積を求めるのに、円の面積公式を使っているわけで、教育的に良くても数学的には瑕疵があります。$


(ii)$\ これを回避するために、面積でなく曲線の長さを用いる方法を検討することにします。$

$それでは、曲線の長さとはなにか。$

　

$曲線を分割したそれぞれの弧に内接する線分の長さの和が、$
$分割を細かくしたとき極限値を もてばその値が曲線の長さと$
$定義されます。$

$この曲線の長さについて$

$(ア)\ 曲線の長さは内接する折れ線の長さよりも長い。$
$(すでに(2)で、左の不等号を示すときに使っています。）$

$(イ)\ 分割を細かくすることで、曲線の長さと折れ線の長さの差をいくらでも小さくできる。$
$（これは極限値の本来の意味）$

$の２つは基本的に受け入れる内容と考えます。$

　

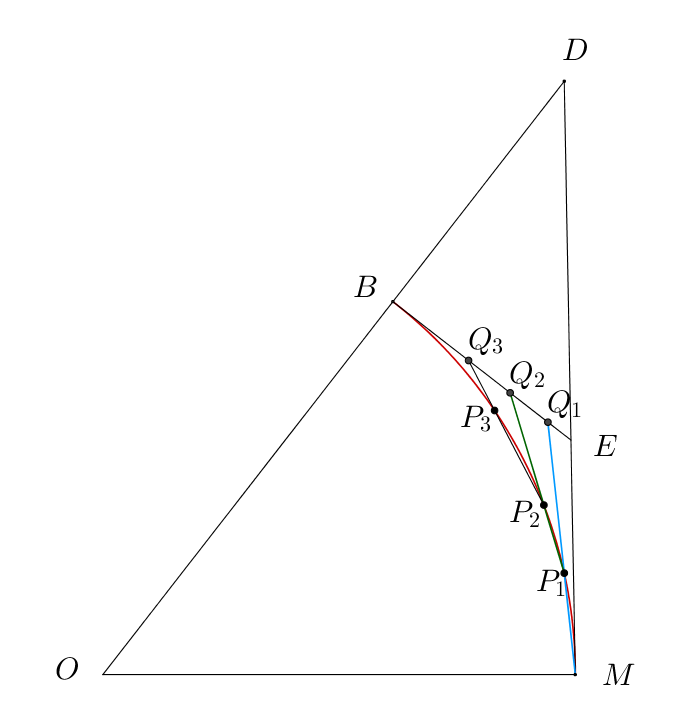
$点 B における接線と（円における接線は微分法を使わずに定義される）$
$MDとの交点をEとする。$

$∠DBE=90° だから 　ED > EB$
$（大きい角に対する辺は大きい\quad $ 三角形の辺と角の定理を参照)

$よって$
$\hspace{2em} MD=ME+ED>ME+EB$
$\hspace{1em}$ 　
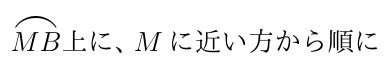
$\hspace{2em} P_0=M,P_1,P_2,\cdots , P_n=B 　をとり、$
$\hspace{2em} P_{k-1}P_k の延長とEBとの交点をQ_k とする。ただし、Q_0=E \ である。$

$△P_kQ_kQ_{k+1}について$

$\hspace{2em} P_kQ_{k+1} < P_kQ_k+Q_kQ_{k+1} 　（三角不等式）$

$\hspace{2em} P_kQ_{k+1}=P_kP_{k+1}+P_{k+1}Q_{k+1} 　だから$

$\hspace{2em}P_kP_{k+1}+P_{k+1}Q_{k+1} < P_kQ_k+Q_kQ_{k+1}$

$\hspace{2em} k=0 　のとき　 P_0P_1+P_1Q_1 < P_0Q_0+Q_0Q_1$
$\hspace{2em} k=1 　のとき　 P_1P_2+P_2Q_2 < P_1Q_1+Q_1Q_2$
$\hspace{2em} k=2 　のとき　 P_2P_3+P_3Q_3 < P_2Q_2+Q_2Q_3$
$\hspace{5em} \vdots $
$\hspace{2em} k=n-1 　のとき　 P_{n-1}P_n+P_nQ_n < P_{n-1}Q_{n-1}+Q_{n-1}Q_n$

$辺々加えて　P_nQ_n=BB=0 　だから$

$\hspace{2em} P_0P_1+ P_1P_2+\cdots +P_{n-1}P_n < P_0Q_0+(Q_0Q_1+Q_1Q_2+\cdots +Q_{n-1}Q_n)$

$\hspace{1em} \therefore \quad MP_1+ P_1P_2+\cdots +P_{n-1}B < ME+EB $

$一方、(イ)より$
　
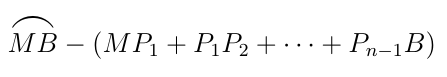
$はnが十分大きければ、ほとんど0に近い値になるから、ED-EB\ より小さくできる。$
$よって$
　
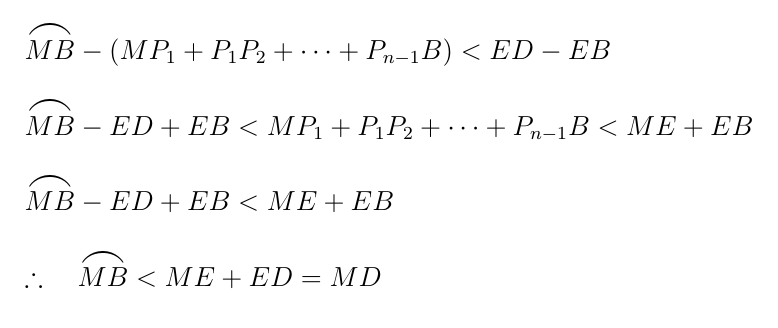
$よって、外接正n角形の１つの辺のCDと弧ABについて$
$\hspace{2em}$　
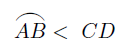
$この関係がすべての辺について成りたつから、その和をとって$

$\hspace{3em} 円Oの円周 < B_n$

$\hspace{4em}\therefore \hspace{1em} 2\pi < B_n$

$これで、面積を使わずに、右側の不等号が証明できました。$



ページの先頭へ↑




アルキメデスの方法　に戻る


メインメニュー　に戻る