2次曲線の媒介変数表示



１　楕円


$(1)三角関数を用いた表示$

　

$線分OPとx軸の正方向のなす角を\theta とすると$

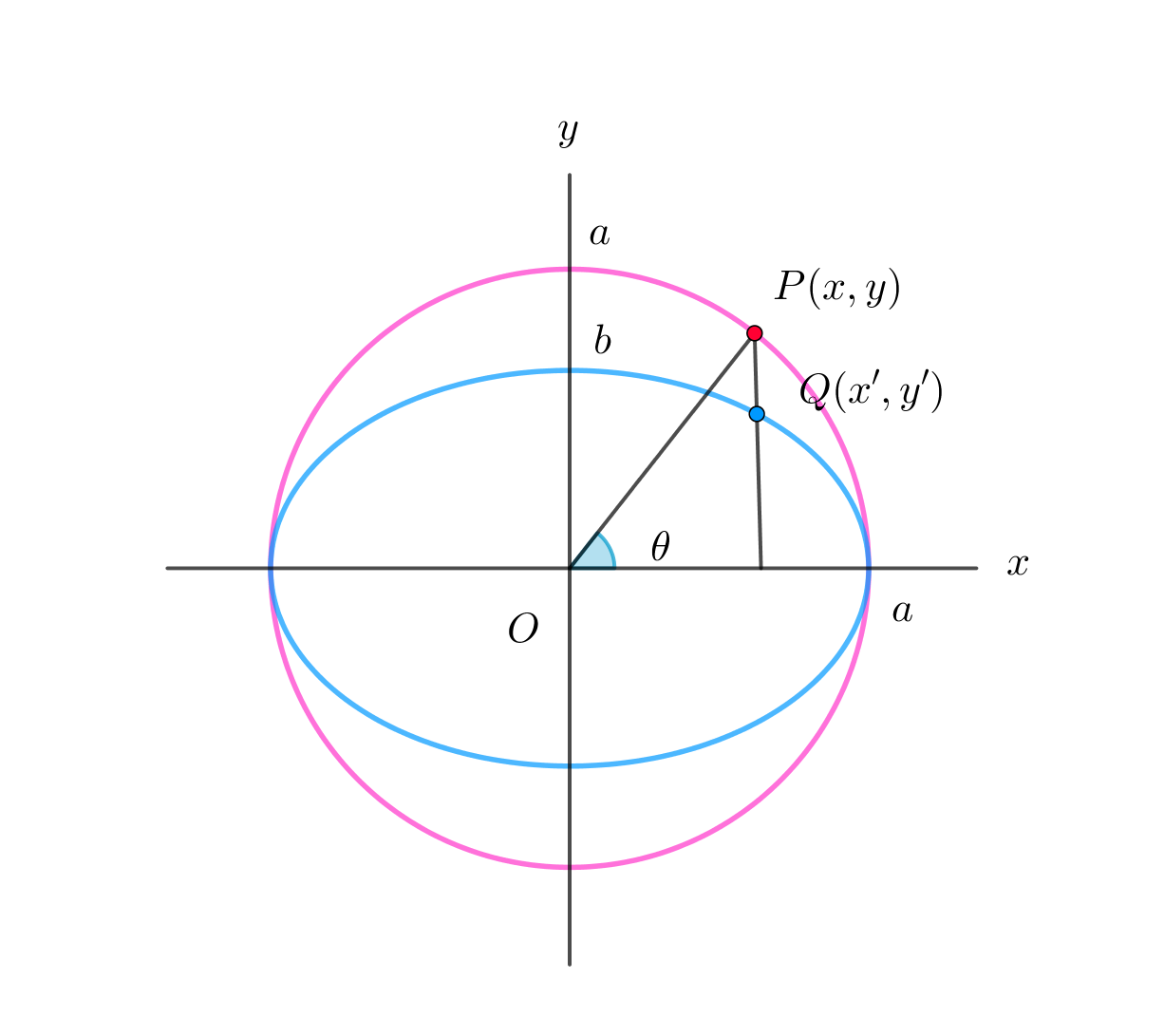
$\quad x=a\cos \theta, \quad y=a\sin \theta 　は円の媒介変数表示である。$

$円　x^2+y^2=a^2 \ \ 上の点P(x,y)をy軸方向に \ \cfrac{b}{a} 倍に縮小した点 \ Q(x,y)は$
$楕円　\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1 　上の点であるから$
$\quad x=a\cos \theta, \quad y=b\sin \theta 　が楕円の媒介変数表示である。$


$(2)有理関数を用いた表示$

　

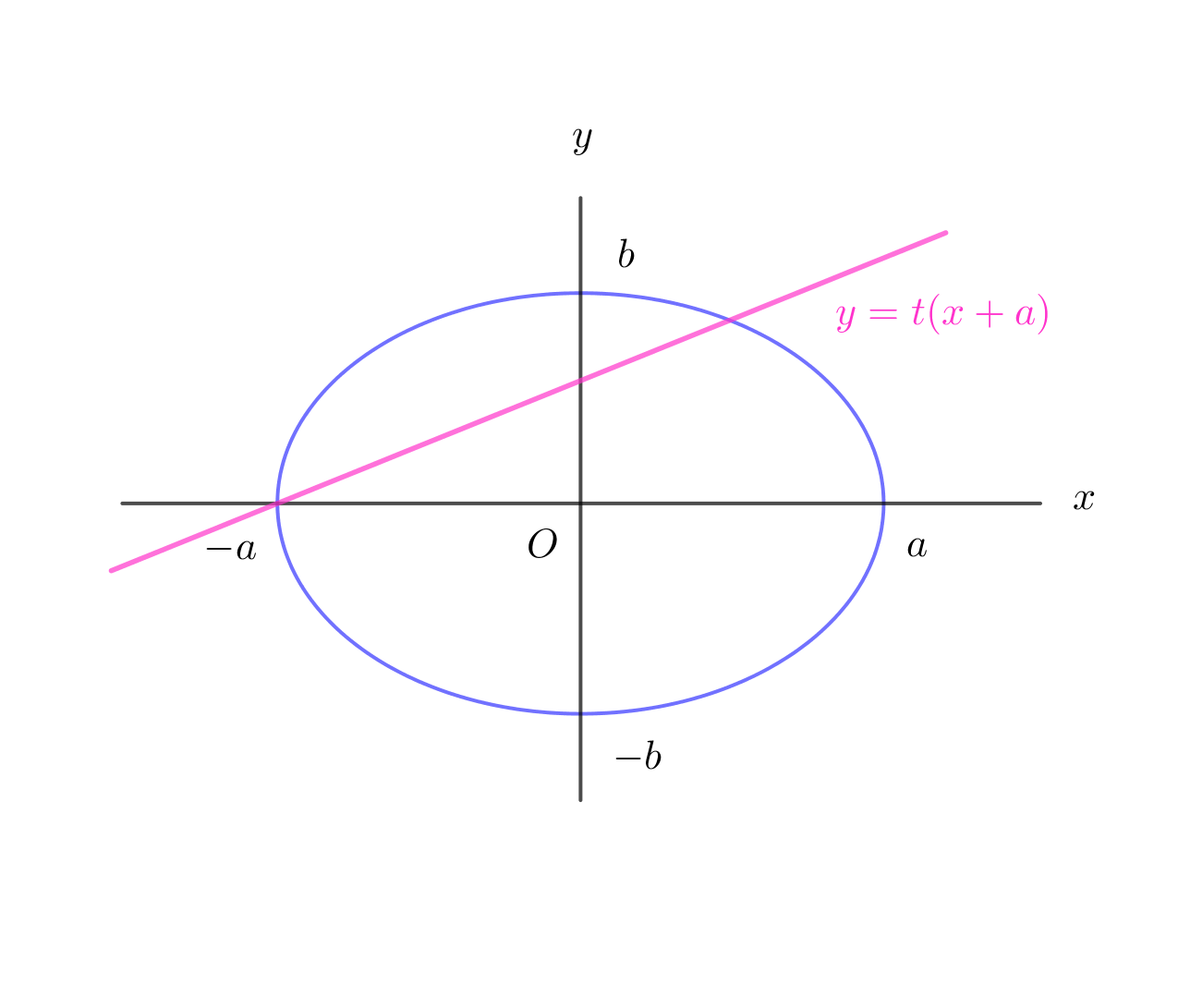
$楕円　\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1 　と点(-a,0) を通る傾きtの$
$直線 \ \ y=t(x+a) の交点は$
\[ \left\{ \begin{array}{l} \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\\ \ \ y=t(x+a)\\ \end{array} \right. \] $\quad b^2x^2+a^2t^2(x+a)^2=a^2b^2$
$\quad b^2(x^2-a^2)+a^2t^2(x+a)^2=0$
$\quad (x+a)\{b^2(x-a)+a^2t^2(x+a)\}=0$
$\quad x \ne -a \ \ より \quad b^2(x-a)+a^2t^2(x+a)=0$
$\quad (b^2+a^2t^2)x+a^3t^2-ab^2=0$

$\quad \therefore x=\cfrac{a(b^2-a^2t^2)}{b^2+a^2t^2}$

$\quad y=t\big(\cfrac{a(b^2-a^2t^2)}{b^2+a^2t^2}+a\big)=\cfrac{2ab^2t}{b^2+a^2t^2}$

$これがtを媒介変数とした、楕円の有理関数表示です。$

$ただし、点(-a,0)は表せません。(t \rightarrow \infty の場合ですが)$



2　双曲線


　
$(1)\ \ 三角関数を用いた表示$

$\quad \cfrac{1}{\cos ^2 \theta}=1+\tan ^2\theta \quad だから$

$\quad x=\cfrac{1}{\cos \theta},\quad y=\tan \theta \quad とおくと \quad x^2-y^2=1 $

$\quad よって \quad 点P(\cfrac{1}{\cos \theta},\ \tan \theta)\ \ はこの双曲線上の点である。$

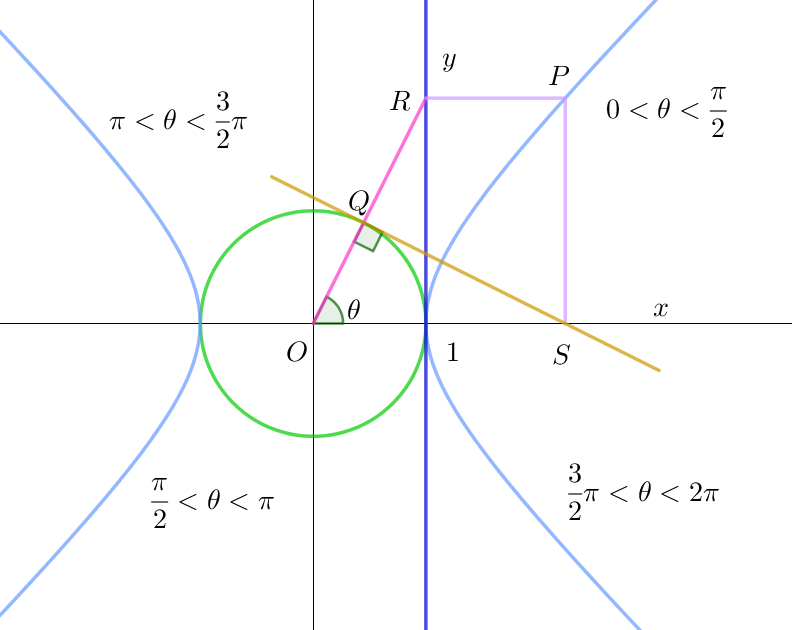
$右図はこれの図形上の説明です。$
$単位円周上に角 \ \theta \ の点 \ Q をとる。点 \ Q における接線のx軸との交点が \ S(\cfrac{1}{\cos \theta},\ 0)$
$また、OQ\ の延長と直線 \ x=1 \ との交点を \ R\ とすると \ \ R(1,\ \tan \theta)$
$点 \ S\ を通り、y\ 軸に平行な直線と、点 \ R\ を通り \ x\ 軸に平行な直線との交点 \ P\ は\ \ P(\cfrac{1}{\cos \theta},\ \tan \theta)$

$\quad \cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1\quad において \quad X=\cfrac{x}{a},\quad Y=\cfrac{y}{b} \quad とおくと$

$\quad X^2-Y^2=1 \quad となるから \quad \cfrac{x}{a}=\cfrac{1}{\cos \theta},\quad \cfrac{y}{b}=\tan \theta \quad とおくと$

$\quad x=\cfrac{a}{\cos \theta} ,\quad y=b\tan \theta \quad は\quad \cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1 \quad 上の点である。$


$(2)\ \ 有理関数を用いた表示$

　

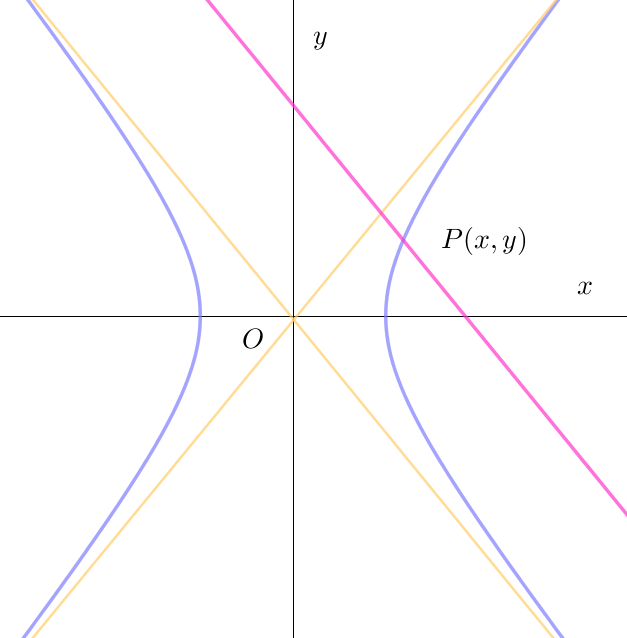
$\quad 双曲線 \ \ \cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1 \quad と漸近線に平行な直線$
$\ \ y=-\cfrac{b}{a}x+t \ \ (t \ne 0)\ \ の交点は$
\[ \left\{ \begin{array}{l} \cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1\\ \ \ y=-\cfrac{b}{a}x+t\\ \end{array} \right. \] $\quad b^2x^2-a^2(-\cfrac{b}{a}x+t)^2=a^2b^2$

$\quad b^2x^2-(b^2x^2-2abtx+a^2t^2)=a^2b^2$

$\quad 2abtx=a^2(t^2+b^2)$

$\quad x=\cfrac{a}{2}(\cfrac{t}{b}+\cfrac{b}{t})$

$\quad y=-\cfrac{b}{a} \times \cfrac{a}{2}(\cfrac{t}{b}+\cfrac{b}{t})+t=\cfrac{b}{2}(\cfrac{t}{b}-\cfrac{b}{t})$

$\quad これが \ t\ を媒介変数とした、有理関数表示です。$


$(3)\ \ 双曲線関数を用いた表示$

$\quad y=\sinh x=\cfrac{e^x-e^{-x}}{2},\quad y=\cosh x=\cfrac{e^x+e^{-x}}{2}\ \ を双曲線関数といい。$

$\qquad 双曲線関数については ($ 双曲線関数$をご覧ください)$

\begin{eqnarray*} \cosh ^2x - \sinh ^2x &=&\big(\cfrac{e^x+e^{-x}}{2}\big)^2-\big(\cfrac{e^x-e^{-x}}{2}\big)^2\\ \\ &=&\cfrac{1}{4}(e^{2x}+2+e^{-2x})-\cfrac{1}{4}(e^{2x}-2+e^{-2x})\\ \\ &=&1\\ \end{eqnarray*}
$\quad したがって、\quad 点P(\cosh t ,\ \sinh t) \ は双曲線 \ \ x^2-y^2=1 \ \ 上の点です。$

$\quad そこで、x=\pm a\cosh t,\quad y=b\sinh t \quad とおけば　\quad \cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1　となります。$


3　放物線


　
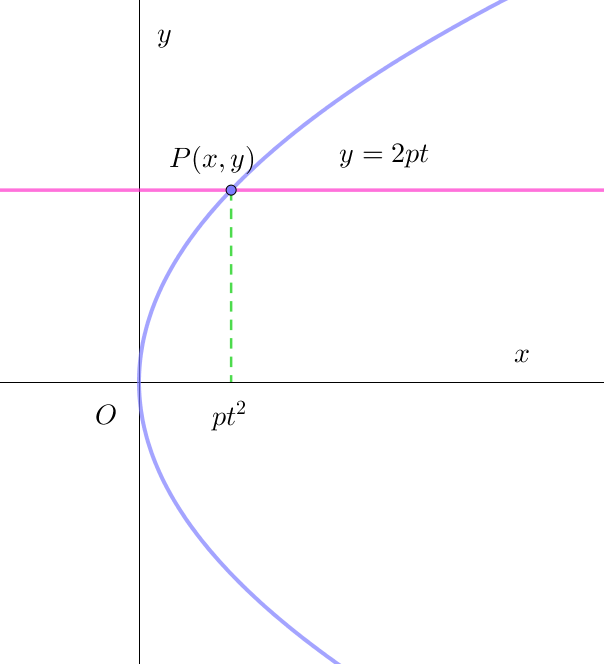
$放物線 \quad y^2=4px \quad と直線 \quad y=2pt \quad との交点は$

$(2pt)^2=4px \quad より \quad 　x=pt^2 \quad だから$

$\quad x=pt^2, \quad y=2pt \quad は放物線の媒介変数表示である。$


ページの先頭へ↑



2次曲線メニュー　に戻る


メインメニュー　に戻る