順序集合
1 順序
$集合Mの元の間に、つぎの条件を満たす関係 \ \prec \ があるとき、これを順序(全順序)といいます。$
$順序の公理$
$\quad Mの任意の元a,\ bについて$
$\qquad (1)\ \ a \prec b,\ \ a=b,\ \ b \prec a \ \ のうちのどれか1つだけが成りたつ。\hspace{3em}(三一律)$
$\qquad (2)\ \ a \prec b ,\ \ b \prec c \ \ ならば a \prec c \hspace{17em}(推移律) $
$\qquad (注) \ \ b \prec a \ \ を \ \ a \succ b \ \ ともかく。$
$自然数、整数、有理数、実数はいずれも大小関係 < (>)を順序にもつ順序集合です。$
$定理$
$複素数Cは任意の元 \alpha =a+b\ i,\ \ \beta =c+d\ i \ \ (a,b,c,dは実数)に対して次のように$
$関係 \prec を定めるとCは順序集合となる。$
$(1)\ \ a < c \ \ のとき \ \ \alpha \prec \beta $
$(2)\ \ a=c \ \ のとき$
$\quad $(i)$\quad b=d \ \ ならば \ \ \alpha =\beta $
$\quad $(ii)$\ \ b < d \ \ ならば \ \ \alpha \prec \beta $
$(証明)$
$(1)\ \ 三一律は、a,b,c,d\ の大小関係によって$
$\quad $(i)$\ \ a < c\ \ のとき \ \ \alpha \prec \beta $
$\quad $(ii)$\ \ a > c\ \ のとき \ \ \alpha \succ \beta $
$\quad a=c \ \ かつ $
$\quad $(iii)$\ \ b=d \ \ のとき \quad \alpha =\beta $
$\quad $(iv)$\quad b < d \ \ のとき \quad \alpha \prec \beta $
$\quad $(v)$\quad \ \ b > d\ \ のとき \quad \alpha \succ \beta $
$のように、a \prec b,\ \ a=b,\ \ b \prec a \ \ のうちのどれか1つだけが成りたつ。$
$(2)\ \ 推移律は、$
$複素数Cの任意の元 \gamma =e+f\ i\ \ (e,fは実数)とする。$
$\quad \alpha \prec \beta , \quad \beta \prec \gamma \ \ とすると$
$\quad \alpha \prec \beta \ \ より \qquad $(i)$\ \ \ a < c \ \ または \ \ $(ii)$\ a = c \ \ かつ \ \ b < d$
$\quad \beta \prec \gamma \ \ より \qquad $(iii)$\ \ c < e \ \ または \ \ $(iv)$\ c = e \ \ かつ \ \ d < f$
$組合わせ方は4通りあるが$
(i)(iii)$のとき \quad a < e \quad となって \quad \alpha \prec \gamma $
(i)(iv)$のとき \quad a < e \quad となって \quad \alpha \prec \gamma $
(ii)(iii)$のとき \quad a < e \quad となって \quad \alpha \prec \gamma $
(ii)(iv)$のとき \quad a = e \ \ かつ \ \ b < f \quad となって \quad \alpha \prec \gamma $
$よって、\alpha \prec \beta,\quad \beta \prec \gamma \ \ ならば \ \ \alpha \prec \gamma \ \ がなりたつから、推移律が成りたつ。$
$(1)(2)より、Cは \ \ \prec \ \ で順序集合となる。$
$ただし、Cは順序体ではないことに注意してください。$(順序体$を参照してください。)$
2 半順序
$集合Mの元の間に、つぎの条件を満たす関係 \ \prec \ があるとき、これを半順序といいます。$
$半順序の公理$
$\quad Mの任意の元a,\ bについて$
$\qquad (1)\ \ a \ne b \ \ のとき、a \prec b または \quad b \prec a \quad または どちらも成りたたない \ \ の3つのうち$
$\hspace{3em}どれか1つだけが成りたつ。$
$\qquad (2)\ \ a \prec b ,\ \ b \prec c \quad ならば \quad a \prec c \hspace{10em}(推移律)$
$例1$
$自然数の集合Nの2数a,bで、bがaの約数であるとき、$
$すなわち \ \ b|a \ \ のとき b \prec a \ \ と表すことにする。$
$b|a,\ \ a|c \quad ならば \quad b|c \quad だから$
$推移律 \ \ b \prec a ,\quad a \prec c \quad ならば \quad b \prec c \quad は成りたつ。$
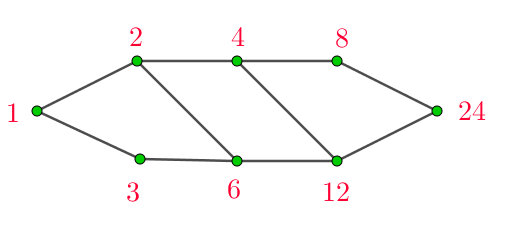
$a=24\ のとき \ \ 約数の集合は\{1,2,3,4,6,8,12,24\} である。$
$b|24,\ b'|24 \ \ で \ \ b|b' \ \ のとき \ \ b ― b' \ \ のように線で結ぶことにする。$
$2と12は、4または6を経由して線で結ばれている。(推移律が成りたつ)$
$3 \nmid 4,\quad 6 \nmid 8 \ \ だから \ \ 3 \nprec 4 ,\quad 6 \nprec 8 \ \ となり線で結べない。$
$すべての約数の関係は右図のとおりで、半順序となります。$
$なお、順序は1本線で結ばれる（そこで線形順序ともいわれる)が、半順序はこのような図になります。$
$例2$
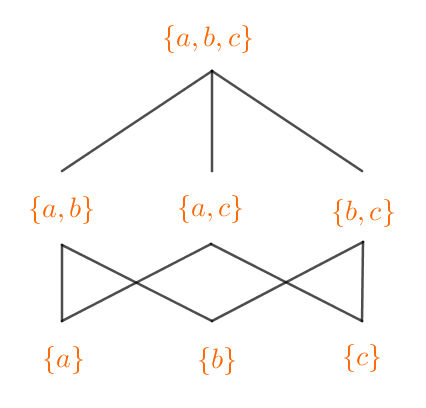$集合\{a,b,c\}の部分集合において、 包含関係 \ \ A \subset B \ \ があれば$
$A― B と線で結ぶことにするが、\{a\} と\{b,c\}のように包含関係が$
$ない場合は線で結ばない。$
$集合の包含関係は推移律が成りたつ。$
$すべての部分集合について包含関係は右図のとおりで、$
$包含関係 \ \ A \subset B \ \ は半順序となります。$
メインメニュー に戻る