MY MATH NOTE

大阪大学(理系) 2021年　問題2

$空間内に、同一平面上にない \ 4 点 \ O,\ A,\ B,\ C\ がある。s,\ t\ を \ 0 < s < 1, \ 0 < t < 1 \ をみたす実数とする。$
$線分 \ OA\ を \ 1:1\ に内分する点を \ A_0,\ 線分 \ OB\ を \ 1:2\ に内分する点を \ B_0,\ 線分 \ AC\ を \ s:(1-s)\ に内分$
$する点を \ P,線分 \ BC\ を \ t:(1-t)\ に内分する点を \ Q\ とする。さらに \ 4\ 点 A_0,\ B_0,\ P,\ Q\ が同一平面上に$
$あるとする。$
$(1)\ \ t\ を \ s\ を用いて表せ。$
$(2)\ \ |\vec{OA}|=1,\ |\vec{OB}|=|\vec{OC}|=2,\ \angle AOB=120°,\ \angle BOC=90°,\ \angle COA=60°,\ \angle POQ=90°であるとき$
$\qquad s\ の値を求めよ。$

(1)

　
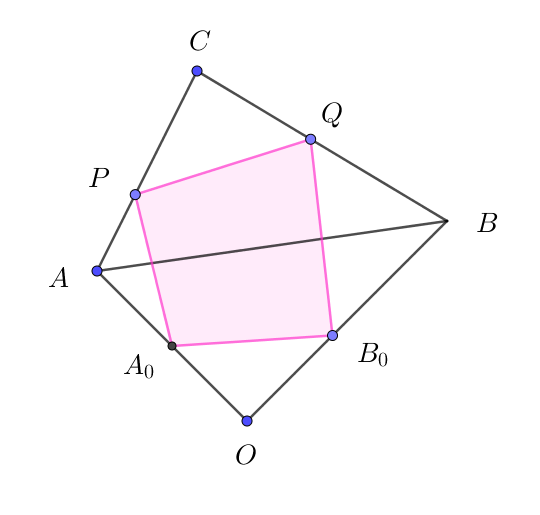
$点 \ A.\ B,\ C\ の点 \ O\ を始点とする位置ベクトルをそれぞれ \ \ \vec{a},\ \vec{b},\ \vec{c}\ \ とおくと$

$\qquad \vec{OA_0}=\cfrac{1}{2}\vec{a},\quad \vec{OB_0}=\cfrac{1}{3}\vec{b},\quad \vec{OP}=(1-s)\vec{a}+s\vec{c},\quad \vec{OQ}=(1-t)\vec{b}+t\vec{c}$

$4\ 点 A_0,\ B_0,\ P,\ Q\ が同一平面上にあるから$

$\quad \vec{A_0Q}=\alpha \vec{A_0B_0}+\beta \vec{A_0P} \quad とおける。$

$\hspace{2em}(このことについては($ベクトルの分解$)を参考にしてください。)$

$よって$

$\quad \vec{OQ}-\vec{OA_0}=\alpha (\vec{OB_0}-\vec{OA_0})+\beta (\vec{OP}-\vec{OA_0}) $

$\quad (1-t)\vec{b}+t\vec{c}-\cfrac{1}{2}\vec{a}= \alpha\big(\cfrac{1}{3}\vec{b}- \cfrac{1}{2}\vec{a}\big)+\beta\big\{(1-s)\vec{a}+s\vec{c}-\cfrac{1}{2}\vec{a}\big\}$

$\quad -\cfrac{1}{2}\vec{a}+(1-t)\vec{b}+t\vec{c}= \big\{-\cfrac{1}{2}\alpha +\beta(1-s)-\cfrac{1}{2}\beta \big\}\vec{a}+ \cfrac{\alpha}{3}\vec{b}+\beta s \vec{c}$

$4\ 点 \ O,\ A,\ B,\ C\ のうち、3\ 点が同じ直線上にあれば、この直線と他の1点で定まる平面上に \ 4\ 点がある$
$ことになるから、どの \ 3\ 点もが同じ直線上にない。すなわち\ \ \vec{a},\ \vec{b},\ \vec{c}\ は \ \vec{0}でなく、どの \ 2\ つのベクトルも$
$平行でない。すなわち、一次独立である。$

$したがって$

\[ \hspace{1em} \left\{ \begin{array}{l} -\cfrac{1}{2}=-\cfrac{1}{2}\alpha +\beta(1-s)-\cfrac{1}{2}\beta \hspace{6em}①\\ 1-t=\cfrac{\alpha}{3}　\ \hspace{13em}②\\ t=\beta s \hspace{16em}③\\ \end{array} \right. \]
$\quad ②より \quad \alpha =3(1-t), \qquad ③より \quad \beta=\cfrac{t}{s} \quad これらを①に代入して$

$\qquad -\cfrac{1}{2}=-\cfrac{3}{2}(1-t)+\cfrac{t(1-s)}{s}-\cfrac{t}{2s}$

$分母を払って、整理すると$

$\quad st+t-2s=0 \qquad t(s+1)=2s \qquad \therefore \ \ t=\cfrac{2s}{s+1}$

(2)

　
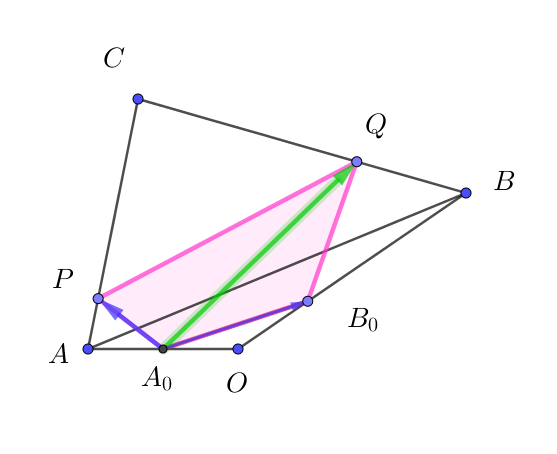
$条件(題意)より$

$ \quad |\vec{a}|=1,\quad |\vec{b}|=|\vec{c}|=2$

$ \quad \vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos 120°=1 \times 2 \times (-\cfrac{1}{2})=-1$

$ \quad \vec{a}\cdot \vec{c}=|\vec{a}||\vec{c}|\cos 60°=1 \times 2 \times \cfrac{1}{2}=1$

$ \quad \vec{b}\cdot \vec{c}=0$

$\vec{OP} \perp \vec{OQ} \quad より \quad \vec{OP}\cdot \vec{OQ}=0 \quad だから$

$ \quad \{(1-s)\vec{a}+s\vec{c}\}\cdot \{(1-t)\vec{b}+t\vec{c}\}=0$

$ \quad (1-s)(1-t)\vec{a}\cdot \vec{b} + t(1-s)\vec{a}\cdot \vec{c} + s(1-t)\vec{b}\cdot \vec{c} + st|\vec{c}|^2=0$

$ \quad -(1-s)(1-t) + t(1-s) +4st=0$

$ \quad -1+2t+s+2st=0$

$(1)\ より \quad t=\cfrac{2s}{s+1} \quad を代入して$

$ \quad -1+\cfrac{4s}{s+1} + s + \cfrac{4s^2}{s+1}=0$

$ \quad 5s^2+4s-1=0 \qquad (5s-1)(s+1)=0 \qquad 0 < s < 1 \quad だから \quad s=\cfrac{1}{5}$

$このとき \quad t=\cfrac{2 \times \dfrac{1}{5}}{\dfrac{1}{5}+1}=\cfrac{1}{3}$

$これは \quad 0 < t < 1 \quad をみたすから \quad s=\cfrac{1}{5}$

ページの先頭へ↑