ベクトルの分解
１ 平面上の場合
$\quad 3\ 点 \ O,\ A,\ B\ に対して、\vec{OA}=\vec{a},\ \vec{OB}=\vec{b}\ とする。\vec{a}\ と \ \vec{b}\ が \ \vec{0}\ でなく、平行でないとき \ (一次独立$
$\quad といいます)、この \ 3\ 点で作られる平面上の任意のベクトル \ \ \vec{OP}=\vec{p}\ \ は$
$\hspace{5em} \ \ \vec{p}=s\vec{a} + t\vec{b} \ \ (s,\ t\ は実数)$
$\quad と表すことができ、この表し方はただ \ 1\ 通りである。$
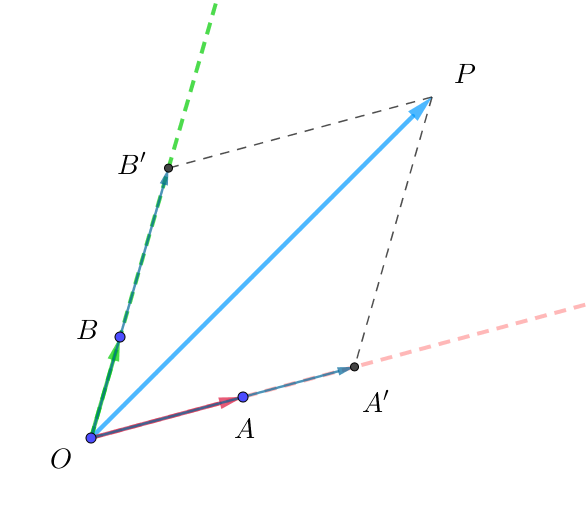$(証明)$
$右図のように、線分OAの延長上に点A'を、線分OBの延長上に点B'をとり、$
$OPを対角線とする平行四辺形OA'PB' をつくる。$
$\qquad \vec{OA'}=s\vec{OA}=s\vec{a},\quad \vec{OB'}=t\vec{OB}=t\vec{b}$
$を満たす実数 \ s,\ t\ が存在するので$
$\qquad \vec{OP}=\vec{OA'}+\vec{OB'}=s\vec{a}+t\vec{b}$
$また、\vec{p}=s\vec{a}+t\vec{b}=s'\vec{a}+t'\vec{b}\ \ (s',\ t'\ は実数)\ \ と \ 2\ 通りに表されたすると$
$(1)\ \ s \ne s' \quad ならば \quad \vec{a}=\cfrac{t'-t}{s-s'}\vec{b} $
$\quad $(i)$\ \ t=t' \quad とすると \quad \vec{a}=\vec{0} \quad となり、\vec{a} \ne \vec{0}\ \ に反する。$
$\quad $(ii)$\ \ t \ne t' \quad とすると \quad \vec{a} /\!/\vec{b} \quad となって、やはり仮定に反する。$
$\quad よって、s=s' \quad である。$
$(2)\ \ このとき \quad t\vec{b}=t'\vec{b} \quad となるから \quad (t-t')\vec{b}=\vec{0}$
$\qquad \vec{b} \ne \vec{0} \quad だから \quad t=t'$
$(1),\ (2)\ より \quad s=s',\ \ t=t' \quad となり \quad \vec{p}=a\vec{a} + t\vec{b} \quad の表し方はただ \ 1\ 通りである。$
$なお、この表し方を、\vec{p}\ の \ \vec{a},\ \vec{b}\ 方向への分解といいます。$
２ 空間の場合
$\quad 同じ平面上にない \ 4\ 点 \ O,\ A,\ B\ ,C\ に対して、\vec{OA}=\vec{a},\ \vec{OB}=\vec{b},\ \vec{OC}=\vec{c}\ \ とする。\vec{a}\ ,\ \vec{b}\ ,\ \vec{c}\ が \ \vec{0}\ でなく、$
$\quad どの2つのベクトルも互いに平行でないとき \ (一次独立といいます)、任意のベクトル \ \ \vec{OP}=\vec{p}\ \ は$
$\hspace{5em} \vec{p}=s\vec{a} + t\vec{b}+u\vec{c} \ \ (s,\ t\ ,uは実数)$
$\quad と表すことができ、この表し方はただ \ 1\ 通りである。$
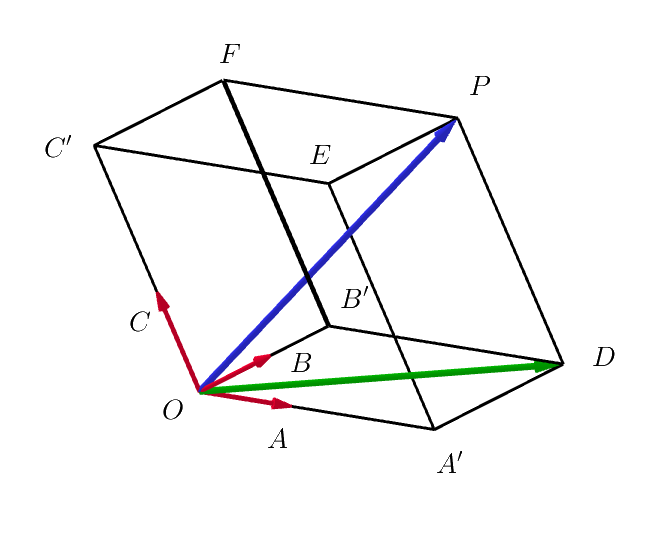$(証明)$
$右図のように、線分 \ OP\ を対角線とする平行六面体$
$OA'DB'-C'EPF \ \ をつくる。$
(i)$\ \ 点 \ D\ は平面 \ OA'B'\ 上にあるから、(1)より$
$\quad \vec{OD}=s\vec{a}+t\vec{b} \quad となる実数 \ s,\ t\ がただ \ 1\ つ存在する。$
(ii)$\ \ \vec{DP} /\!/\vec{OC} \quad だから \quad \vec{DP}=u\vec{c} \quad となる実数 \ u\ がただ \ 1\ つ存在する。$
$\vec{OP}=\vec{OD}+\vec{DP} \quad だから$
$\qquad \vec{p}=s\vec{a}+t\vec{b}+u\vec{c}\quad となる実数 \ s,\ t,\ u\ がただ \ 1\ つ存在する。$
$例$
$3\ 点 \ A(1, -1,\ 0),\ B(3,\ 1,\ 2),\ C(2,\ 2, -1)\ を通る平面の方程式$
$(1)\quad 上の説明による解法$
$\quad \vec{AB}=(3,\ 1,\ 2)-(1, -1,\ 0)=(2,\ 2,\ 2) \qquad \vec{AC}=(2,\ 2, -1)-(1, -1,\ 0)=(1,\ 3, -1)$
$\quad 平面上の任意の点を \ P(x,\ y,\ z) \quad とおくと$
$\qquad \vec{AP}=s\vec{AB}+t\vec{AC}\ \ (s,\ t\ は実数)\ \ とおけるから$
$\qquad (x,\ y,\ z)-(1, -1,\ 0)=s(2,\ 2,\ 2)+t(1,\ 3, -1)$
\[
\hspace{1em}
\left\{ \begin{array}{l}
x-1=2s+t \ \hspace{5em}(1)\\
y+1=2s+3t \hspace{5em}(2)\\
z=2s-t \ \hspace{7em}(3)\\
\end{array} \right.
\]
$\quad (1)-(2)\quad より \quad x-y-2=-2t \hspace{5em}(4)$
$\quad (1)-(3)\quad より \quad x-z-1=2t \hspace{6em}(5)$
$\quad (4)+(5) \quad より \quad 2x-y-z-3=0$
$(2)\quad 法線ベクトルによる解法$
$\quad 法線ベクトルを \quad \vec{n}=(a,\ b,\ c)\quad とおくと$
$\quad \vec{AB} \perp \vec{n} \quad より \quad \vec{AB}\cdot \vec{n}=2a+2b+2c=0 \qquad a+b+c=0 \hspace{5em}(1)$
$\quad \vec{AC} \perp \vec{n} \quad より \quad \vec{AC}\cdot \vec{n}=a+3b-c=0 \hspace{14em}(2)$
$\quad (1)+(2)\ \ より \quad 2a+4b=0 \qquad a=-2b$
$\quad (1)に代入して \quad -2b+b+c=0 \qquad c=b$
$\quad よって \vec{n}=(-2b,\ b,\ b) \quad とくに \quad b=1 \quad とおくと \quad \vec{n}=(-2,\ 1,\ 1)$
$\quad \vec{AP} \perp \vec{n} \quad より \quad (x-1,\ y+1,\ z) \cdot (-2,\ 1,\ 1)=0$
$\quad -2(x-1)+(y+1)+z=0 \qquad \therefore \ \ 2x-y-z-3=0$
メインメニュー に戻る