お茶の水女子大学 2021年 A問題1
$a > b > 0\ \ として、座標平面上の楕円 \ \ \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\ \ を \ C\ とおく。C\ 上の点 \ P(p_1,\ p_2)\ \ (p_2 \ne 0)\ における$
$C\ の接線を \ l,法線を \ n\ とする。$
$(1)\ \ 接線 \ l\ および法線 \ n\ の方程式を求めよ。$
$(2)\ \ 2点 \ A(\sqrt{a^2-b^2},\ 0),\ \ B(-\sqrt{a^2-b^2},\ 0)\ に対して、法線 \ n\ は \ \angle APB \ の二等分線であることを示せ。$
$(解説)$
$(1)\ \ 接線の傾きmは、重解条件から求められます。法線は接線に直交します。$
$(2)\ \ 三角形の内角の二等分線と辺の比の関係を用いる方法があります。$
(1)
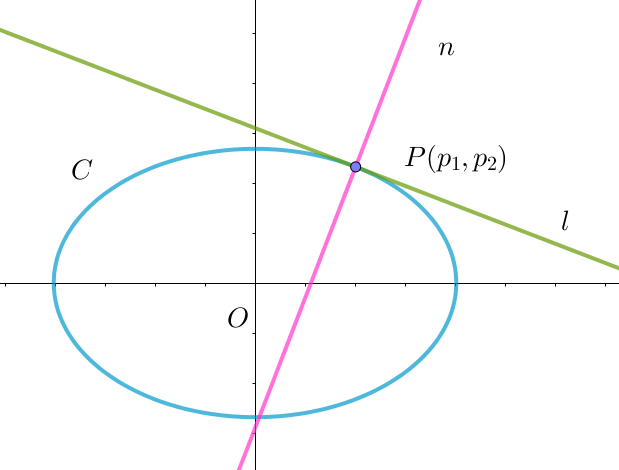
(i)$\ \ 点 \ P(p_1,\ p_2)\ における接線 \ l\ は$
$方法 \ 1 \quad 傾き \ m\ を重解条件から求める方法$
$\quad y=m(x-p_1)+p_2 \quad とおくと、楕円との交点は$
$\quad \cfrac{x^2}{a^2}+\cfrac{(mx-(mp_1-p_2))^2}{b^2}=1$
$\quad (a^2m^2+b^2)x^2-2a^2m(mp_1-p_2)x+a^2(mp_1-p_2)^2-a^2b^2=0$
$\quad x=p_1\ \ を重解にもつから、解と係数の関係より$
$\quad p_1+p_1=\cfrac{2a^2m(mp_1-p_2)}{a^2m^2+b^2}$
$\quad p_1(a^2m^2+b^2)=a^2m(mp_1-p_2)$
$\quad m=-\cfrac{b^2p_1}{a^2p_2}$
$方法 \ 2 \quad 傾き \ m\ を微分法で求める方法$
$\quad \cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\ \ の両辺を \ x\ で微分して$
$\quad \cfrac{2x}{a^2}+\cfrac{2yy'}{b^2}=0 \qquad \therefore \ \ y'=-\cfrac{b^2x}{a^2y}$
$\quad よって接線の傾きは \quad m=-\cfrac{b^2p_1}{a^2p_2}$
$接線の方程式は$
$\quad y=-\cfrac{b^2p_1}{a^2p_2}(x-p_1)+p_2$
$\quad 両辺に \ \ \cfrac{p_2}{b^2} \ \ をかけて$
$\quad \cfrac{p_2}{b^2}y=-\cfrac{p_1}{a^2}(x-p_1)+ \cfrac{p_2^2}{b^2}$
$\quad \therefore \ \ \cfrac{p_1}{a^2}x + \cfrac{p_2}{b^2}y=\cfrac{p_1^2}{a^2}+ \cfrac{p_2^2}{b^2}=1$
(ii)$\ \ 点 \ P(p_1,\ p_2)\ における法線 \ n\ は$
$\quad y=\cfrac{a^2p_2}{b^2p_1}(x-p_1)+p_2$
$\quad 両辺に \ \ \cfrac{p_1}{a^2} \ \ をかけて$
$\quad \cfrac{p_1}{a^2}y=\cfrac{p_2}{b^2}(x-p_1)+ \cfrac{p_1p_2}{a^2}$
$\quad \therefore \ \ \cfrac{p_2}{b^2}x - \cfrac{p_1}{a^2}y=p_1p_2\big(-\cfrac{1}{a^2}+ \cfrac{1}{b^2}\big)$
(2)
$楕円 \ C\ の離心率 \ e\ は \quad e=\cfrac{\sqrt{a^2-b^2}}{a}\quad だから \quad a^2-b^2=a^2e^2$
$法線 \ n\ が \ x\ 軸と交わる点を \ Q(q,\ 0)\ とすると$
$\quad \cfrac{p_2}{b^2}q =p_1p_2\big(-\cfrac{1}{a^2}+ \cfrac{1}{b^2}\big) \quad より \quad q=p_1b^2\big(-\cfrac{1}{a^2}+ \cfrac{1}{b^2}\big)=p_1 \times \cfrac{a^2-b^2}{a^2}=e^2p_1$
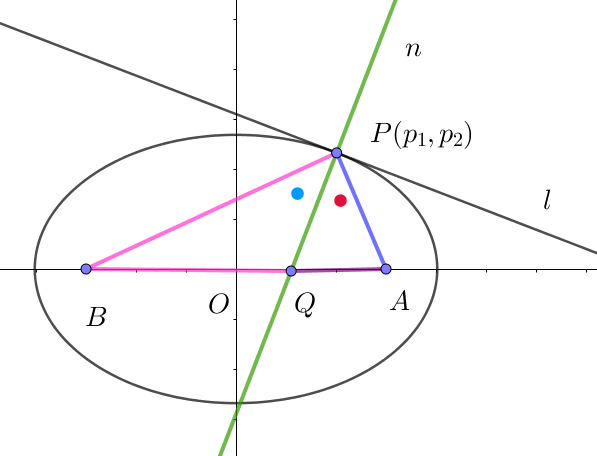
$\quad A(ae,\ 0),\ B(-ae,\ 0) \ \ だから$
$\quad AQ=ae-e^2p_1=e(a-e p_1),\qquad BQ=e^2p_1+ae=e(a+e p_1)$
$\quad \cfrac{AQ}{BQ}=\cfrac{e(a-e p_1)}{e(a+e p_1)}=\cfrac{a-e p_1}{a+e p_1}$
$一方$
$\quad PA=a-ep_1,\quad PB=a+ep_1 \quad だから \quad \cfrac{PA}{PB}=\cfrac{AQ}{BQ}$
$\qquad このことについては($楕円$)を参考にしてください。ここでは計算は省略します。$
$よって、\triangle APB \ \ における \ \ \angle P\ の二等分線と辺の比の定理の逆より$
$線分PQ、すなわち点 \ P\ における法線 \ n\ は \angle APB\ を二等分する。$
$\qquad このことについては($三角形の内角・外角の二等分線の性質$)を参考にしてください。$
メインメニュー に戻る