正規乱数列の作成方法
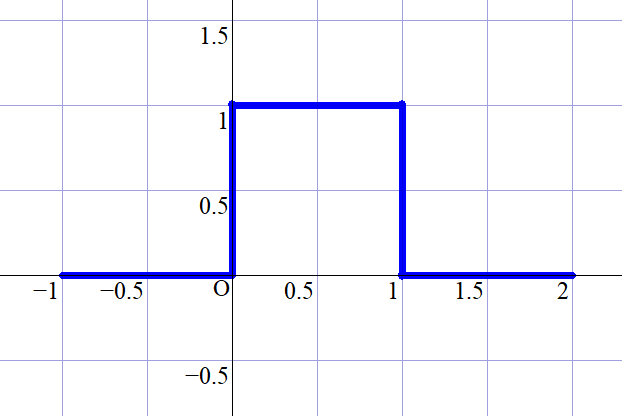
$区間[0,1]上の一様分布の確率密度関数は$
\[f(x)=
\left\{ \begin{array}{l}
0 \hspace{3em} (x < 0,\ \ x > 1)\\
1 \hspace{3em} (0 \leqq x \leqq 1 )\\
\end{array} \right.
\]
$だから$
\[平均は \quad E(x)=\int _{-\infty}^{\infty}xf(x)dx=\int _0^1xdx=\cfrac{1}{2}\]
\[分散は \quad V(x)=\int _{-\infty}^{\infty}(x-\cfrac{1}{2})^2f(x)dx=\int _0^1(x-\cfrac{1}{2})^2dx=\cfrac{1}{12}\]
$したがって、一様乱数列から取ったn個の平均 \ \ \overline{X_n}=\cfrac{X_1+X_2+\cdots +X_n}{n} \ \ は$
$中心極限定理$(中心極限定理)$より、nが十分大きいときは平均 \cfrac{1}{2},分散 \cfrac{1}{12n} の正規分布 N(\cfrac{1}{2},\cfrac{1}{12n}) で近似できます。$
$正規化して \quad z=\cfrac{\overline{X_n}-\dfrac{1}{2}}{\sqrt{\dfrac{1}{12n}}} \ \ はN(0,1)にしたがいます。$
$とくに、n=12とすると$
$\quad z=12(\overline{X_{12}}-\cfrac{1}{2})=X_1+X_2+\cdots +X_{12}-6$
$となって計算はいたって簡単になります。まだ電卓がなかった大学1年生の統計学のレポートで、$
$この式を算盤で計算したことがなつかしく思い出されます。$
$今では、スマホで関数電卓アプリが無料で利用できますので、n=12 \ とするまでもなく$
$n=4 \ で十分です。このときは$
$\quad Z=\cfrac{\overline{X_4}-\dfrac{1}{2}}{\sqrt{\dfrac{1}{48}}}=\sqrt{3}(X_1+X_2+X_3+X_4-2) \ \ となります。$
$この\sqrt{3}をかける計算が当時は大変だったのです。$
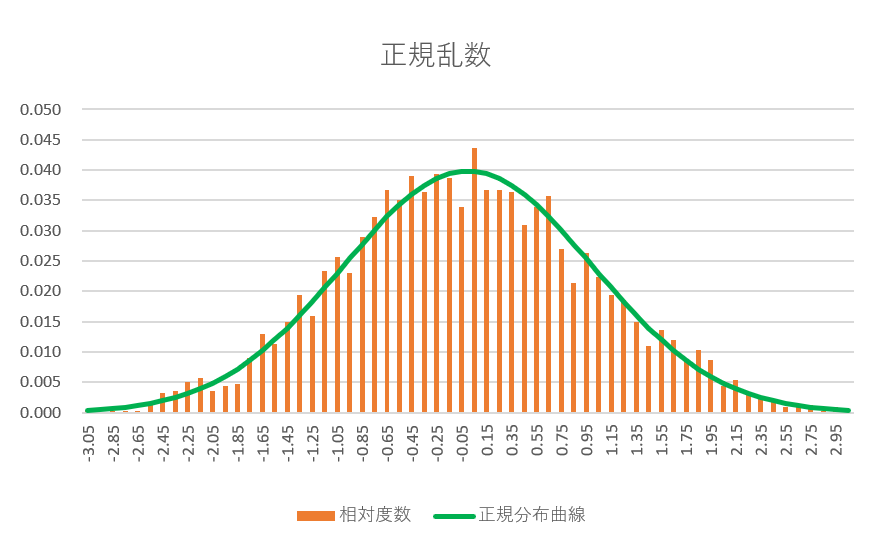
$右は、[0,1]の一様乱数から、n=4として$
$上の方法で、Excel \ VBAで計算したものです。$
$3000個の正規乱数を作って(一瞬です!)$
$相対度数をグラフであらわしたものです。$
$併せて、標準正規分布曲線もかいてあります。$
$これをみるとn=4でも十分使えることがわか$
$ります。$
$適合性の検定(そのうち載せるつもりです)を$
$行えばなおはっきりするかもしれません。$
メインメニュー に戻る