九州大学(理系) 2021年 問題3
$座標平面上の点 \ (x,\ y)\ について、次の条件を考える。$
$\quad 条件:すべての実数 \ t\ に対して \ \ y \leqq e^t-xt \ \ が成立する。 \quad \cdots (*)$
\[以下の問いに答えよ。必要ならば \quad \lim _{x \rightarrow +0} x\log x =0 \quad を使ってよい。\]
$(1)\ \ 条件(*)をもたす点 \ (x,\ y)\ 全体の集合を座標平面上に図示せよ。$
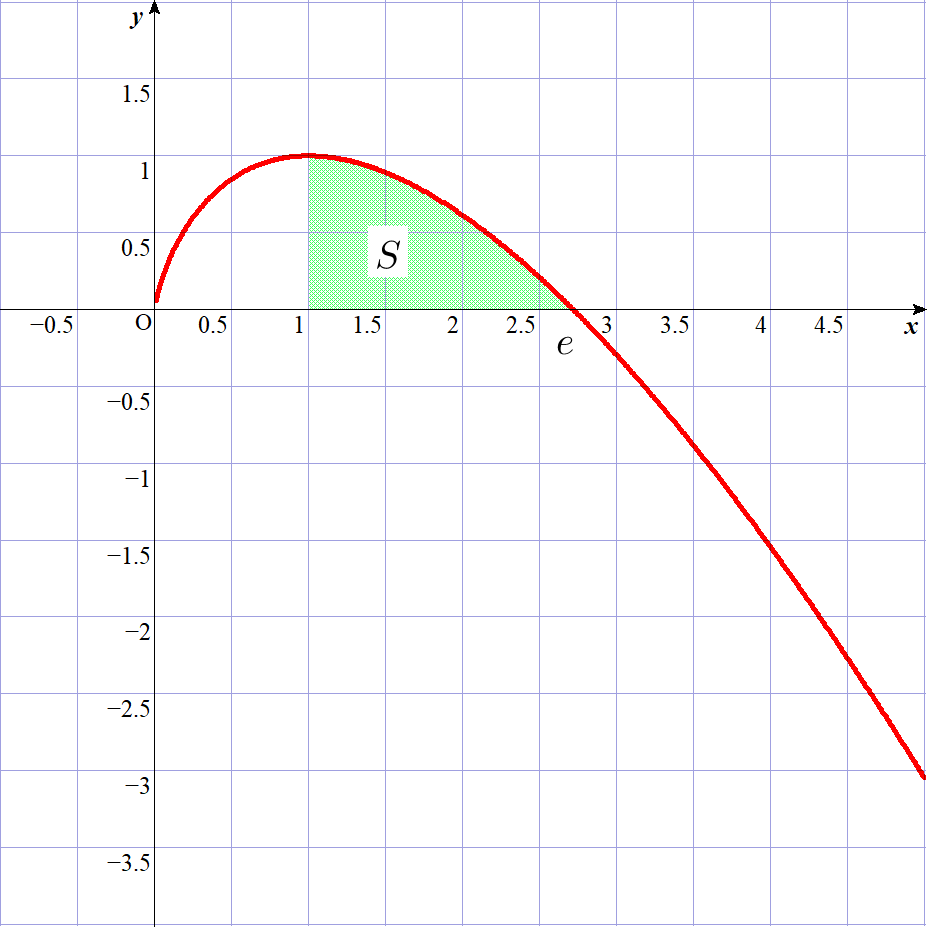
$(2)\ \ 条件(*)をみたす点 \ (x,\ y)のうち、x \leqq 1 \ \ かつ \ \ y \leqq 0 \ \ をみたすものの全体の集合を \ S\ とする。$
$\quad S\ を \ x\ 軸の周りに \ 1\ 回転させてできる立体の体積を求めよ。$
$(解説)$
$(1)は条件が意味する内容が理解できれば、最小値を求めればよいと気づくのではないでしょうか。$
$(2)は回転体の体積を求める定積分を計算するだけです。$
(1)
$\quad y \leqq e^t-xt \quad より \quad e^t-xt -y \geqq 0$
$\quad f(t)=e^t-xt -y \quad とおくと \quad f'(t)=e^t-x \qquad f'(t)=0 \quad より \quad t=\log x$
$\quad f(t) の増減表は$
\[ \begin{array}{c||c|c|c|c|c} t & \cdots & \log x & \cdots \\ \hline f'(t) & - & 0 & +\\ \hline f(t) & \searrow & 極小 & \nearrow \\ \end{array} \]
$\quad f(t)\ は \ \ x =\alpha \ \ で極小かつ最小となり、最小値は \ \ f(\log x)=e^{\log x} -x\log x -y=x-x\log x -y$
$\quad すべての実数 \ t\ に対して \quad e^t-xt -y \geqq 0 \ \ が成りたつのは \ \ f(t)\ の最小値が \ 0\ または正のときであるから$
$\qquad x-x\log x -y \geqq 0$
$\qquad \therefore y \leqq x(1-\log x)$
$\quad g(x)=x(1-\log x) \quad とおくと \quad g'(x)=1-\log x +x(-\cfrac{1}{x})=-\log x$
$g'(x)=0 \quad より \quad x=1$
$g(x) の増減表は$
\[
\begin{array}{c||c|c|c|c|c}
x & 0 & \cdots & 1 & \cdots \\
\hline
g'(x) & & + & 0 & -\\
\hline
g(x) & & \nearrow & 極大 & \searrow \\
\end{array}
\]
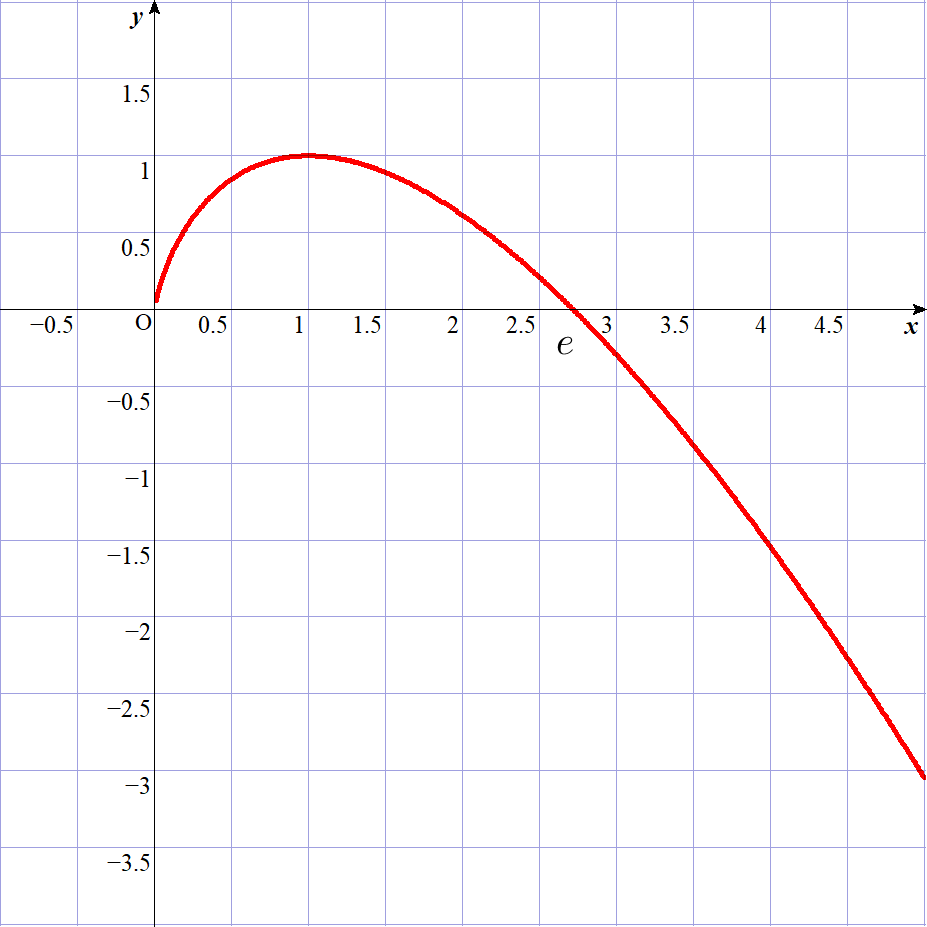
$\quad g(x)\ は \ \ x =1 \ \ で極大となり、極大は \quad g(1)=1-\log 1=1$
$\quad x \longrightarrow +0 \quad のとき \quad x\log x \longrightarrow 0 \quad だから \quad g(x) \longrightarrow 0$
$\quad x\ 軸との交点は \quad g(x)=0 \quad より \quad x=0 \ \ と \ \ x=e\ \ で \ \ グラフは右図のとおり$
\[なお、\quad \lim _{x \rightarrow 0} x\log x=0 \ \ の根拠については\]
$\hspace{5em} ($不定形の極限値(2)$)を参考にしてください。$
(2)
\begin{eqnarray*}
V
&=&\pi\int _1^{\large{e}} y^2dx\\
\\
&=&\pi\int _1^{\large{e}} x^2(1-\log x)^2dx\\
\\
&=&\pi\Big[\cfrac{x^3}{3}(1-\log x)^2\Big] _1^{\large{e}} -\pi\int _1^{\large{e}} \cfrac{x^3}{3} \times 2(1-\log x)(-\cfrac{1}{x})dx\\
\\
&=&-\cfrac{\pi}{3} + \cfrac{2\pi}{3}\int _1^{\large{e}} x^2(1-\log x) dx\\
\\
&=&-\cfrac{\pi}{3} + \cfrac{2\pi}{3}\Big[\cfrac{x^3}{3}(1-\log x)^2\Big] _1^{\large{e}} -\cfrac{2\pi}{3}\int _1^{\large{e}} \cfrac{x^3}{3} (-\cfrac{1}{x})dx\\
\\
&=&-\cfrac{\pi}{3} -\cfrac{2\pi}{9} +\cfrac{2\pi}{9}\int _1^{\large{e}} x^2dx\\
\\
&=&-\cfrac{5\pi}{9} +\cfrac{2\pi}{9}(\cfrac{e^3}{3}-\cfrac{1}{3})\\
\\
&=&\cfrac{\pi}{27}(2\large{e}^3 -17)\\
\end{eqnarray*}
メインメニュー に戻る