九州大学(理系) 2021年 問題1
$座標空間内の \ 4\ 点 \ O(0,\ 0,\ 0),\ A(1,\ 0,\ 0),\ B(0,\ 1,\ 0),\ C(0,\ 0,\ 2)\ を考える。以下の問いに答えよ。$
$(1)\ \ 四面体 \ OABC\ に内接する球の中心の座標を求めよ。$
$(2)\ \ 中心の \ x\ 座標、y\ 座標、z\ 座標がすべて正の実数であり、xy\ 平面、yz\ 平面、zx\ 平面のすべてと接する$
$\quad 球を考える。この球が平面 \ ABC\ と交わるとき、その交わりとしてできる円の面積の最大値を求めよ。$
$(解説)$
$(1)は3つの座標平面に接することから球の中心の座標が半径 \ r\ で表されます。残りの\triangle ABC に接することから$
$\quad この \ r\ を求めます。$
$(2)が(1)と異なるのは外接する場合もあることです。$
(1)
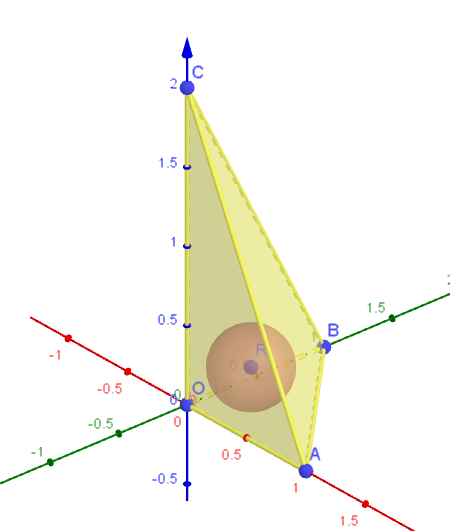
$球は \ xy\ 平面、yz\ 平面、zx\ 平面のすべてと接するから、半径を \ r\ とおくと、$
$中心は \ R(r,\ r,\ r)\ とおける。$
$平面 \ ABC\ を \ \ ax+by+cz=d \quad とおくと$
$\quad A\ (1,\ 0,\ 0)\ \ を通るから \quad a=d$
$\quad B\ (0,\ 1,\ 0)\ \ を通るから \quad b=d$
$\quad C\ (0,\ 0,\ 2)\ \ を通るから \quad 2c=d$
$よって 平面は \quad dx+dy+\cfrac{d}{2}z=d \quad すなわち \quad 2x+2y+z=2$
$この平面の法線ベクトルを、原点 \ O\ から四面体の外に向かう向きの単位ベクトルでとると \quad \vec{n}=(\cfrac{2}{3},\ \cfrac{2}{3},\ \cfrac{1}{3})$
$球は、平面 \ ABC\ とも接するから \ 中心 \ R(r,\ r,\ r)\ とこの平面との距離も \ r\ である。接点を \ H(x_1,\ y_1,\ z_1)とすると$
$\vec{RH}=r\vec{n} \quad だから \quad (x_1-r,\ y_1-r,\ z_1-r)=r(\cfrac{2}{3},\ \cfrac{2}{3},\ \cfrac{1}{3})$
$\quad x_1=r+\cfrac{2}{3}r=\cfrac{5}{3}r,\qquad y_1=r+\cfrac{2}{3}r=\cfrac{5}{3}r,\qquad z_1=r+\cfrac{1}{3}r=\cfrac{4}{3}r$
$H(x_1,\ y_1,\ z_1)\ は平面上の点だから \quad 2x_1+2y_1+z_1=2$
$よって \quad 2 \times \cfrac{5}{3}r + 2 \times \cfrac{5}{3}r + \cfrac{4}{3}r =2 \qquad \therefore \ \ r=\cfrac{1}{4}$
$したがって 球の中心は \quad R\ (\cfrac{1}{4},\ \cfrac{1}{4},\ \cfrac{1}{4})$
$(別解)$
$球は、平面 \ ABC\ とも接するから中心 \ R(r,\ r,\ r)\ とこの平面との距離も \ r\ である。接点を \ H\ とする。$
$この平面 \ \ 2x+2y+z-2=0 \ \ の法線ベクトルを、原点 \ O\ から四面体の外に向かう向きでとると$
$\quad RH=r \ \ で、\vec{RH}\ と \ \vec{n}\ は逆向きであるから \qquad -\cfrac{2r+2r+r-2}{\sqrt{2^2+2^2+1^2}}=r$
$\qquad この公式については($点と平面との距離$)を参考にしてください。$
$\quad -\cfrac{5r-2}{3}=r \quad より \quad r=\cfrac{1}{4}$
(2)
$球は \ xy\ 平面、yz\ 平面、zx\ 平面のすべてと接するから、半径を \ r\ とおくと、中心は \ R(r,\ r,\ r)\ とおける。$
$点 \ R\ から、平面 \ ABC\ に下ろした垂線を \ RH\ とすると$
$\quad RH=\cfrac{|2r+2r+r-2|}{\sqrt{2^2+2^2+1^2}}=\cfrac{|5r-2|}{3}$
$球が平面 \ ABC\ と交わる条件は \quad RH \leqq r \quad だから$
$\quad \cfrac{|5r-2|}{3} \leqq r \qquad すなわち \quad |5r-2| \leqq 3r$
(i)$\ \ r \leqq \cfrac{2}{5} \quad のとき \quad 2-5r \leqq 3r \qquad r \geqq \cfrac{1}{4} \qquad このとき、円の中心は四面体の内部にある。$
(ii)$\ \ r \geqq \cfrac{2}{5} \quad のとき \quad 5r-2 \leqq 3r \qquad r \leqq 1 \qquad このとき、円の中心は四面体の外部にある。$
(i),(ii)$より \quad \cfrac{1}{4} \leqq r \leqq 1$
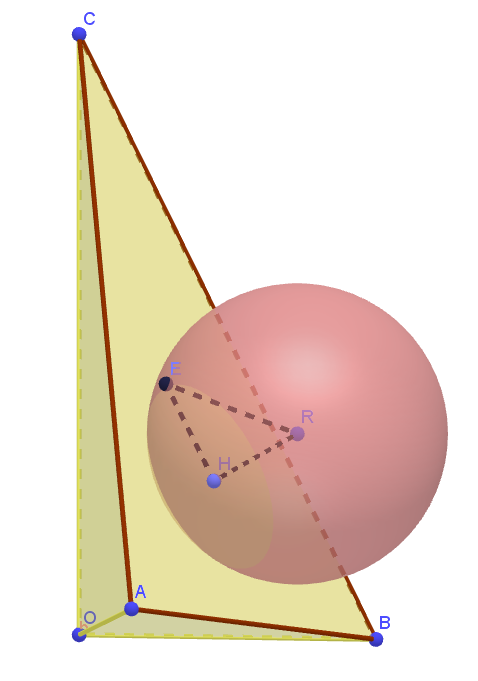
$交わりとしてできる円の半径を \ s\ とすると$
\begin{eqnarray*}
s^2
&=&r^2-RH^2\\
&=&r^2-\big(\cfrac{5r-2}{3}\big)^2\\
&=&-\cfrac{1}{9}(16r^2-20r)-\cfrac{4}{9}\\
&=&-\cfrac{16}{9}(r^2-\cfrac{5}{4}r)-\cfrac{4}{9}\\
&=&-\cfrac{16}{9}\{(r-\cfrac{5}{8})^2-\cfrac{25}{64}\}-\cfrac{4}{9}\\
&=&-\cfrac{16}{9}(r-\cfrac{5}{8})^2+\cfrac{1}{4}\\
\end{eqnarray*}
$\cfrac{1}{4} \leqq r \leqq 1 \quad の範囲で \quad r=\cfrac{5}{8} \ \ のとき 最大となり、最大値は \ \ s^2=\cfrac{1}{4}$
$このとき円の面積は \quad S=\pi s^2=\cfrac{\pi}{4}$
$なお、r=\cfrac{5}{8} \quad だから \ \ 円の中心 \ R\ は四面体の外にある。$
メインメニュー に戻る