点と平面の距離
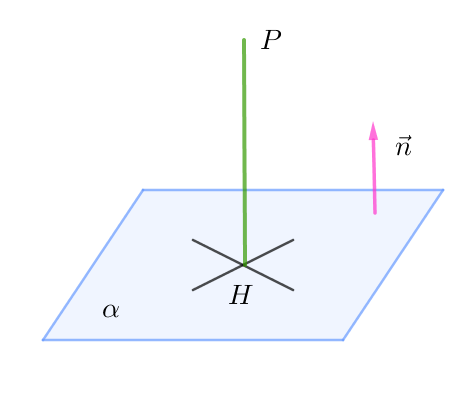
$空間において、点 \ P(x_0,\ y_0,\ z_0)\ から、平面 \ \alpha \ :\ ax+by+cz+d=0 \ \ へ下ろした垂線の長さ$
$(点 \ P\ と平面\ \alpha \ との距離)は$
$\hspace{5em} \cfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}$
$これを \ 3\ 通りの方法で証明しますが、さほど違いはありません。$
$(証明1)$
$垂線の足をH(x_1,\ y_1,\ z_1)\ とすると \quad ax_1+by_1+cz_1+d=0 \hspace{6em}(1)$
$\quad \vec{HP}=(x_0-x_1,\ y_0-y_1,\ z_0-z_1)$
$平面 \ \alpha \ の法線ベクトルは \ \ \vec{n}=(a,\ b,\ c)$
$\vec{HP}\ /\!/ \ \vec{n} \quad より \quad \vec{HP}=k\ \vec{n}\ \ (kは定数) \quad とおけるから$
$\quad (x_0-x_1,\ y_0-y_1,\ z_0-z_1)=k(a,\ b,\ c)$
$\quad x_0-x_1=ka,\quad y_0-y_1=kb,\quad z_0-z_1=kc$
$\therefore x_1=x_0-ka,\quad y_1=y_0 - kb,\quad z_1=z_0 - kc \qquad これらを(1)に代入して$
$a(x_0-ka)+b(y_0-kb)+c(z_0-kc)+d=0$
$ax_0+by_0+cz_0+d-k(a^2+b^2+c^2)=0$
$\quad k=\cfrac{ax_0+by_0+cz_0+d}{a^2+b^2+c^2}$
$よって垂線の長さDは$
$\quad D=|\vec{HP}|=|k\vec{n}|=|\cfrac{ax_0+by_0+cz_0+d}{a^2+b^2+c^2}|\cdot \sqrt{a^2+b^2+c^2}=\cfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}$
$(証明2)$
$点P(x_0,\ y_0.\ z_0)\ を通り、平面 \ \alpha \ に垂直な直線の方向ベクトルは、平面 \ \alpha \ の法線ベクトル \ \ n=(a,\ b,\ c)$
$と向きが一致するからその直線は$
$\qquad \cfrac{x-x_0}{a}=\cfrac{y-y_0}{b}=\cfrac{c-c_0}{c} \hspace{5em}(2)$
$この値を \ t\ とおくと \quad x=x_0+at,\quad y=y_0+bt,\quad z=z_0+ct$
$これは、直線のパラメータ表示である。平面 \ \alpha \ との交点は$
$\qquad a(x_0+at)+b(y_0+bt)+c(z_0+ct)+d=0$
$\qquad ax_0+by_0+cz_0+d+(a^2+b^2+c^2)t=0$
$\qquad t=-\cfrac{ax_0+by_0+cz_0+d}{a^2+b^2+c^2}$
$この \ t\ に対して、交点 \ H(x_1,\ y_1,\ z_1)\ は \ \ x_1=x_0+at,\quad y_1=y_0+bt,\quad z_1=z_0+ct \quad で求まる。$
$したがって点 \ P\ と平面 \ \alpha \ との距離 \ D\ は$
\begin{eqnarray*} D^2 &=&(x_1-x_0)^2+(y_1-y_0)^2+(z_1-z_0)^2\\ \\ &=&(at)^2+(bt)^2+(ct)^2\\ \\ &=&(a^2+b^2+c^2) t^2\\ \\ &=&(a^2+b^2+c^2) \times \big(-\cfrac{ax_0+by_0+cz_0+d}{a^2+b^2+c^2}\big)^2\\ \\ &=&\cfrac{(ax_0+by_0+cz_0+d)^2}{a^2+b^2+c^2}\\ \end{eqnarray*} $\qquad \therefore \ \ D=\cfrac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}$
$(証明3)$
$平面 \ \alpha \ の法線ベクトル \ \vec{n}\ を単位ベクトルでとると \quad \vec{n}=\cfrac{1}{\sqrt{a^2+b^2+c^2}}(a,\ b,\ c)$
(i)$\ \ \vec{HP}\ と \ \vec{n}\ が同じ向きならば \quad \vec{HP}=D\vec{n} \quad だから$
$\qquad (x_0-x_1,\ y_0-y_1,\ z_0-z_1)=D \cdot \cfrac{1}{\sqrt{a^2+b^2+c^2}}(a,\ b,\ c)$
$\qquad x_0-x_1=\cfrac{Da}{\sqrt{a^2+b^2+c^2}},\quad y_0-y_1=\cfrac{Db}{\sqrt{a^2+b^2+c^2}},\quad z_0-z_1=\cfrac{Dc}{\sqrt{a^2+b^2+c^2}}$
$\qquad H(x_1,\ y_1,\ z_1)\ は平面 \ \alpha \ 上の点だから \quad ax_1+by_1+cz_1+d=0$
$\qquad a(x_0-\cfrac{Da}{\sqrt{a^2+b^2+c^2}})+b(y_0-\cfrac{Db}{\sqrt{a^2+b^2+c^2}})+c(z_0-\cfrac{Dc}{\sqrt{a^2+b^2+c^2}})+d=0$
$\qquad ax_0+by_0+cz_0+d=D\big(\cfrac{a^2+b^2+c^2}{\sqrt{a^2+b^2+c^2}}\big)$
$\qquad ax_0+by_0+cz_0+d=D \sqrt{a^2+b^2+c^2}$
$\qquad \therefore \ \ D=\cfrac{ax_0+by_0+cz_0+d}{\sqrt{a^2+b^2+c^2}}$
(ii)$\ \ \vec{HP}\ と \ \vec{n}\ が逆向きならば \quad \vec{HP}=-D\vec{n} \quad だから$
$\qquad D=-\cfrac{ax_0+by_0+cz_0+d}{\sqrt{a^2+b^2+c^2}} \quad となります$
メインメニュー に戻る