神戸大学(理系) 2022年 問題2
$m\ を \ 3\ 以上の自然数、\theta=\cfrac{2\pi}{m},\ C_1\ を半径 \ 1\ の円とする。円 \ C_1\ に内接する(すべての頂点が \ C_1\ 上にある)$
$正 \ m\ 角形を \ P_1\ とし、P_1\ に内接する \ (P_1\ のすべての辺と接する)\ 円を \ C_2\ とする。同様に、n\ を自然数と$
$するとき、円 \ C_n\ に内接する正 \ m\ 角形を\ P_n\ とし、P_n\ に内接する円を \ C_{n+1}\ とする。C_n\ の半径を \ r_n,$
\[C_n\ の内側で \ P_n\ の外側の部分の面積を \ s_n\ とし、f(m)=\sum _{n=1}^{\infty} s_n\ \ とする。以下の問に答えよ。\]
$(1)\ \ r_n,\ s_n\ の値を \ \theta,\ n\ を用いて表せ。$
$(2)\ \ f(m)\ の値を \ \theta \ を用いて表せ。$
\[(3)\ \ 極限値 \ \ \lim _{m \rightarrow \infty} f(m)\ \ を求めよ。ただし、必要があれば \quad \lim _{x \rightarrow 0} \cfrac{x-\sin x}{x^3}=\cfrac{1}{6} \quad を用いてよい。\]
$(解説)$
$(1)\ \ 二等辺三角形において、頂点から底辺に下ろした垂線は頂角を二等分します。$
$(2)\ \ f(m)\ は公比 \ \cos ^2 \cfrac{\theta}{2}\ \ の無限等比級数になります。$
$(3)\ \ 指示された極限値がつかえるように変形します。$
(1)
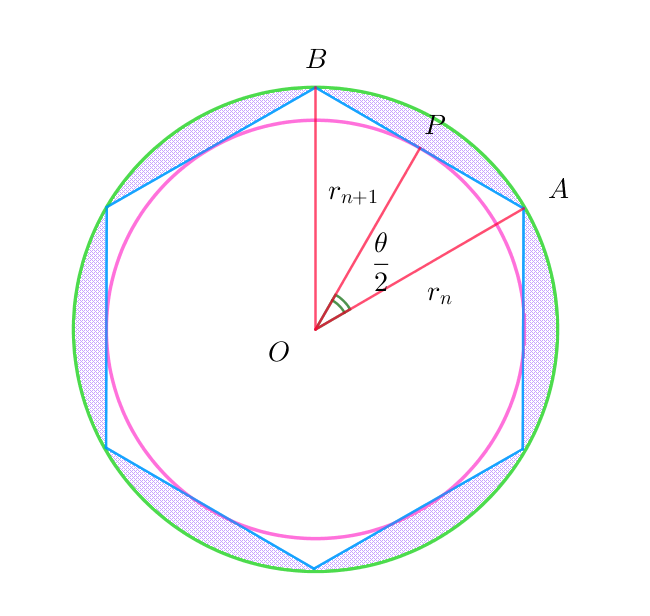
$正 \ m\ 角形 \ P_n\ の辺 \ AB\ は円 \ C_{n+1}\ に接するから接点を \ P\ とすると$
$\qquad OP \perp AB$
$\triangle OAB \ は \ OA=OB \ の二等辺三角形だから \ OP\ は \ \angle AOB\ の二等分線$
$である。よって \quad \angle AOP=\cfrac{\theta}{2}$
$直角三角形 \ OAP \ において \quad OP=OA\cos \cfrac{\theta}{2} \quad だから$
$\quad r_{n+1}=r_n\cos \cfrac{\theta}{2} $
$\quad \therefore \ \ r_n=r_1\cos ^{n-1} \cfrac{\theta}{2} =\cos ^{n-1} \cfrac{\theta}{2}$
\begin{eqnarray*}
\quad
s_n
&=&\pi r_n^2-m\triangle OAB\\
\\
&=&\pi r_n^2-m \times \cfrac{1}{2} \times r_n^2 \times \sin \theta\\
\\
&=&\pi \cos ^{2(n-1)} \cfrac{\theta}{2} - \cfrac{2\pi}{\theta} \times \cfrac{1}{2} \times \cos ^{2(n-1)} \cfrac{\theta}{2} \ \sin \theta\\
\\
&=&\pi \cos ^{2(n-1)} \cfrac{\theta}{2} \ \big(1- \cfrac{\sin \theta}{\theta}\big)\\
\end{eqnarray*}
(2)
\begin{eqnarray*} \quad f(m) &=&\sum _{n=1}^{\infty} s_n\\ \\ &=&\sum _{n=1}^{\infty} \pi \cos ^{2(n-1)} \cfrac{\theta}{2}\ \big(1- \cfrac{\sin \theta}{\theta}\big)\\ \\ &=&\pi \big(1- \cfrac{\sin \theta}{\theta}\big) \sum _{n=1}^{\infty} \cos ^{2(n-1)} \cfrac{\theta}{2}\\ \\ &=&\pi \big(1- \cfrac{\sin \theta}{\theta}\big) \times \cfrac{1}{1-\cos ^2 \dfrac{\theta}{2}}\\ \\ &=&\pi \big(1- \cfrac{\sin \theta}{\theta}\big) \cdot \cfrac{1}{\sin ^2 \dfrac{\theta}{2}}\\ \end{eqnarray*}
(3)
\begin{eqnarray*} \quad f(m) &=&\pi \big(1- \cfrac{\sin \theta}{\theta}\big) \cdot \cfrac{1}{\sin ^2 \dfrac{\theta}{2}}\\ \\ &=&\pi \cdot \cfrac{\theta -\sin \theta}{\theta} \cdot \big(\cfrac{\dfrac{\theta}{2}}{\sin \dfrac{\theta}{2}}\big)^2 \times \cfrac{1}{(\dfrac{\theta}{2}\big)^2}\\ \\ &=&4\pi \cdot \cfrac{\theta -\sin \theta}{\theta ^3} \cdot \big(\cfrac{\dfrac{\theta}{2}}{\sin \dfrac{\theta}{2}}\big)^2 \\ \\ \end{eqnarray*} $したがって$
\[\qquad \lim _{m \rightarrow \infty}f(m)=\lim _{\theta \rightarrow 0} 4\pi \cdot \cfrac{\theta -\sin \theta}{\theta ^3} \cdot \big(\cfrac{\dfrac{\theta}{2}}{\sin \dfrac{\theta}{2}}\big)^2 =4\pi \times \cfrac{1}{6} \times 1=\cfrac{2}{3}\pi\]
$(補足)$
\[\quad 極限値 \quad \lim _{x \rightarrow 0} \cfrac{x-\sin x}{x^3}=\cfrac{1}{6} \quad の求め方は\] $\hspace{3em}$ テーラー展開による不定形の極限値(4)$)をご覧ください。$
メインメニュー に戻る