完全順列
1 完全順列とは
$n \times n$の正方形のますに、次のルールにしたがって○印をつける。
(i) 各行、各列のますには1つの○しか入らない。
(ii)$\quad (1,1),(2,2),\cdots , (n,n)$ の対角線のますには○をつけない。
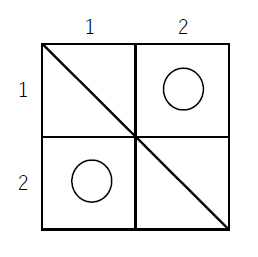
そこで、
第1列は第2行に○印がついているので[2]を対応させ
第2列は第1行に○印がついているので[1]を対応させると
順列(21)が対応します。
なお、$2 \times 2$ のますでは右図のほかには○印をつけられません。
(2)$\quad 3 \times 3$ のますでは下図のように2通りの○印のつけ方があります。
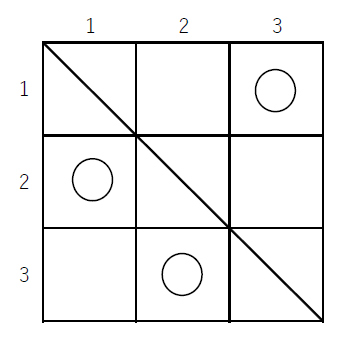
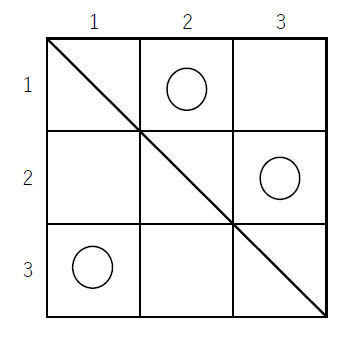
したがって、対応する順列は順に (231),$\ $ (312) です。
(3)$\quad 4 \times 4$ のますでは下図のように9通りの○印のつけ方があります。
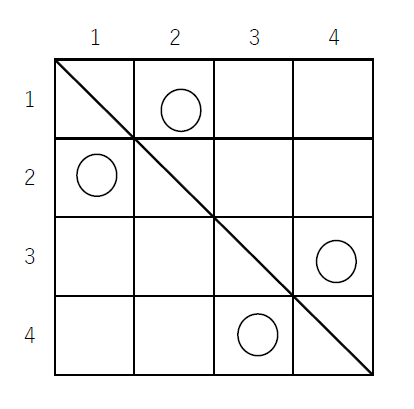
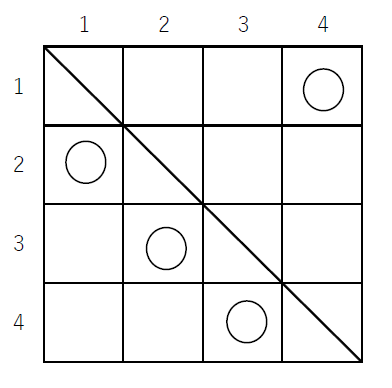
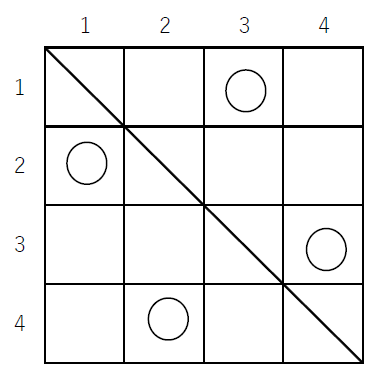
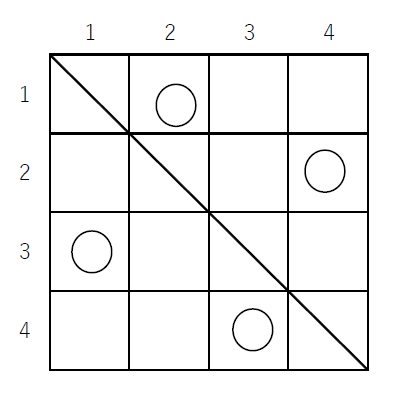
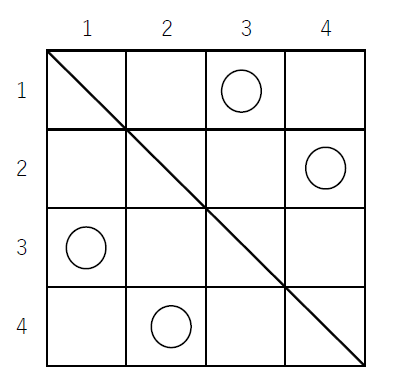
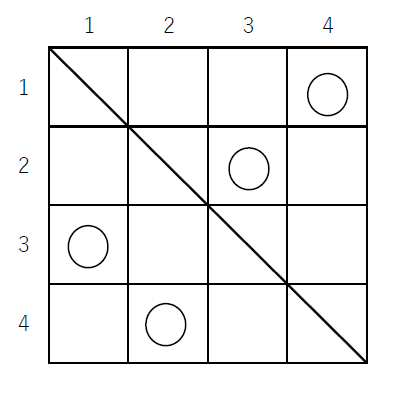
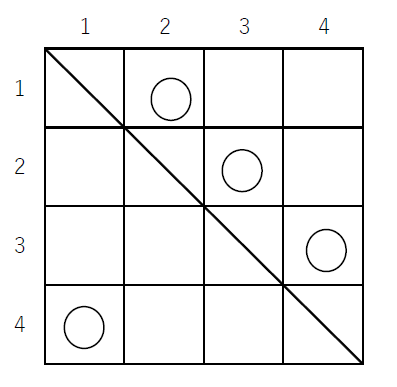
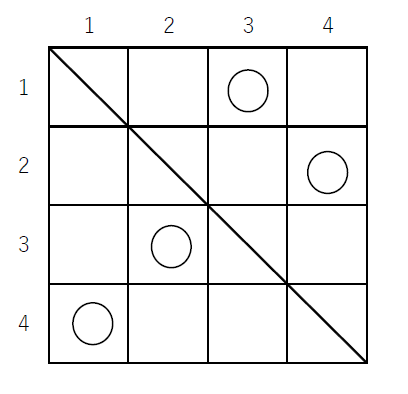
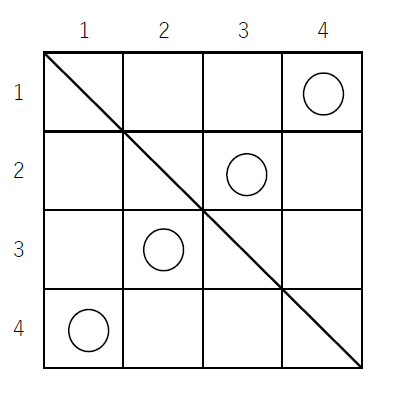
対応する順列は順に
$\hspace{2em} (2143),\ (2341),\ (2413),\ (3142),\ (3412),\ (3421),\ (4123),\ (4312),\ (4321)$
です。
このようにして得られた$\quad n \times n \quad $ますにつけた○印に対応する順列を『完全順列』といいます。
上のルールを順列のことばで言い換えると
完全順列とは
$\hspace{2em} 1からnまでの数字を1列に並べたとき、左からk番目の数字がkではない$
ような並べ方
具体的な例をあげます。
(1)手紙の問題
$n$個の手紙と、その宛名を書いた$n$枚の封筒がある。手紙を封筒に入れるとき、
『どの手紙も宛名が一致しないような入れ方』
(2)プレゼント交換の問題
$n$人があるパーティーで持ち寄ったプレゼントを交換するとき、
『自分が持ってきたプレゼントに当たらないような組み合わせ方』
これらは完全順列の代表的な例です。
2 完全順列の総数を求める漸化式
一般に$n$個の完全順列の総数を「モンモール数」といいます。
モンモールはフランスの数学者の名前です。
ここではその総数を$f(n)$と表すことにして、プレゼント交換の問題を考えながら$f(n)$の満たす
漸化式を導きましょう。
今パーティーに参加した人を $a_1,a_2,\cdots , a_n$ とし、持ち寄ったプレゼントを $b_1,b_2,\cdots , b_n$
とします。このとき完全順列の総数は$f(n)$です。
$a_1\ はb_1\ 以外のプレゼントを受け取るから、それを\ b_k \ (2 \leqq k \leqq n)\ とすると(n-1)通りあります。$
$このとき参加者 \ a_k \quad (2 \leqq k \leqq n)\ $ は
$\quad $(i)$\ b_1$ をもらう
$\quad $(ii)$\ b_1$をもらわない
のどちらかであるからそれぞれについて完全順列の総数は
(i)のとき
$\quad プレゼントの残りは\ b_k\ と\ b_1\ を除く(n-2)個あります。$
$\quad これらを、a_kとa_1を除く(n-2)人の参加者が自分の持ってきたプレゼントに当たらなければ$
$\quad よいから f(n-2)\ 通りあります。$
(ii)のとき
$\quad プレゼントの残りはb_kを除く(n-1)個あります。$
$\quad これらを、a_1を除く(n-1)人の参加者が自分の持ってきたプレゼントに当たらなければ$
$\quad よいから f(n-1)\ 通りあります。$
(i),(ii)より$\hspace{1em} f(n)=(n-1)\{f(n-1)+f(n-2)\}$
ここで、$n \rightarrow n+1$ とおくと
$\hspace{2em} f(n+1)=n\{f(n)+f(n-1)\}$
これで$f(n)$の満たす漸化式が導かれました。
ただし、上の例から $f(1)=0,\ f(2)=1$ です。
3 漸化式の解の求め方
わかりやすくするために $f(n)=a_n$ とおくと、漸化式は
$\quad a_{n+1}=n(a_n+a_{n-1}) ただし a_1=0,\ a_2=1$
これを変形して
$\quad a_{n+1}-(n+1)a_n=-(a_n-n\ a_{n-1})$
$\hspace{2em} a_{n+1}-(n+1)a_n=b_n とおくと$
$\quad b_n=-b_{n-1} \quad b_1=a_2-2a_1=1$
$\quad \therefore b_n=b_1 \times (-1)^{n-1}=(-1)^{n-1}=(-1)^{n+1}$
よって
$\quad a_{n+1}-(n+1)a_n=(-1)^{n+1}$
両辺を$(n+1)!\ $で割って
$\quad \cfrac{a_{n+1}}{(n+1)!}-\cfrac{a_n}{n!}=\cfrac{(-1)^{n+1}}{(n+1)!}$
$\hspace{2em} \cfrac{a_n}{n!}=c_n$ とおくと
$\quad c_{n+1}-c_n=\cfrac{(-1)^{n+1}}{(n+1)!} ただし c_1=\cfrac{a_1}{1!}=0$
これは階差数列だから
$\quad n \geqq 2$のとき
\[c_n=c_1+\sum _{k=1}^{n-1}\cfrac{(-1)^{k+1}}{(k+1)!}=\cfrac{1}{2!}-\cfrac{1}{3!}+ \cdots +\cfrac{(-1)^n}{n!}\] よって
$\hspace{2em} a_n=n!\ c_n=n!\ \{\cfrac{1}{2!}-\cfrac{1}{3!}+ \cdots +\cfrac{(-1)^n}{n!}\}$
これで完全順列の総数(モンモール数)が求まりました。
いくつかの$n$について求めてみると
$\quad a_3=3!(\cfrac{1}{2!}-\cfrac{1}{3!})=3-1=2$
$\quad a_4=4!(\cfrac{1}{2!}-\cfrac{1}{3!}+\cfrac{1}{4!})=12-4+1=9$
となって確かに上で求めた値に一致します。
後は値だけ書きますが
$\quad a_5=44 ,\quad a_6=265,\quad a_7=1854, \quad \cdots$
となります。
メインメニュー に戻る