金沢大学(理系) 2025年　問題1


$実数 \ m>1 \ \ について、座標平面上に \ 3\ 点A(1,\ 0),\ B(m,\ 0),\ C(m^2,\ 0)\ \ をとる。点P(x,\ y)\ は $
$AP:CP=1:m \ \ を満たしながら動くとする。次の問いに答えよ。$
$(1)\ \ 点P(x,\ y)\ \ の軌跡を求めよ。$
$(2)\ \ 次の等式を証明せよ。 \qquad \vec{PB} \cdot \vec{PC}=m(m+1)(m-x)$
$(3)\ \ y \ne 0 \ \ とする。点P(x,\ y)\ \ に対して \quad \angle APB=\angle BPC \ \ が成り立つことを示せ。$


(1)

　

$AP:CP=1:m \ \ より \quad CP=mAP$

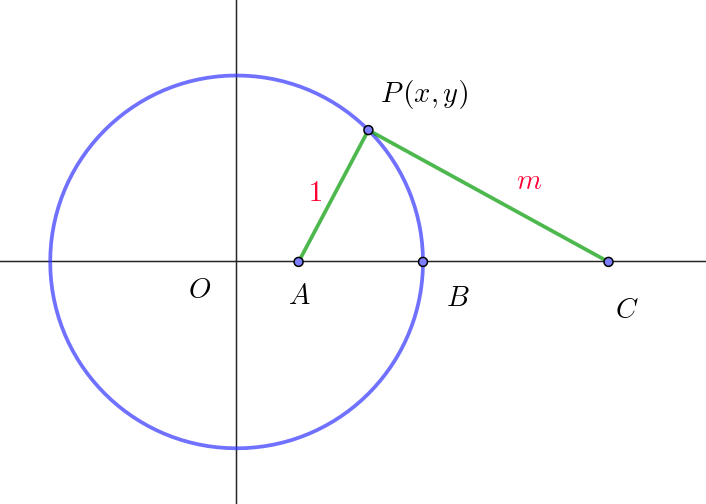
$\therefore \ \ CP^2=m^2AP^2$

$(x-m^2)^2+y^2=m^2\{(x-1)^2+y^2\}$

$(m^2-1)x^2+(m^2-1)y^2=m^4-m^2$

$(m^2-1)(x^2+y^2)=m^2(m^2-1)$

$m>1 \ \ だから \quad m^2-1 > 0$

$\therefore \ \ x^2+y^2=m^2$

$点P(x,\ y)\ \ の軌跡は原点中心、半径 \ m\ の円。$


(2)


\begin{eqnarray*} & &\vec{PB} \cdot \vec{PC}\\ \\ &=&(m-x,-y)\cdot (m^2-x,-y)\\ \\ &=&(m-x)(m^2-x)+y^2\\ \\ &=&m^3-m^2x-mx+(x^2+y^2)\\ \\ &=&m^3-m^2x-mx+m^2\\ \\ &=&m(m^2-mx-x+m)\\ \\ &=&m\{m(m-x)+(m-x)\}\\ \\ &=&m(m+1)(m-x) \end{eqnarray*}

(3)


$(2) と同様に$

\begin{eqnarray*} & &\vec{PA} \cdot \vec{PB}\\ \\ &=&(1-x,-y)\cdot (m-x,-y)\\ \\ &=&(1-x)(m-x)+y^2\\ \\ &=&m-x-mx+x^2+y^2\\ \\ &=&m-x-mx+m^2\\ \\ &=&(m-x)+m(m-x)\\ \\ &=&(m+1)(m-x) \end{eqnarray*}
$(2)より \quad \vec{PB} \cdot \vec{PC}=m(m+1)(m-x) \quad だから$

$m\vec{PA} \cdot \vec{PB}=\vec{PB} \cdot \vec{PC}$

$m \cdot PA \cdot PB \cos \angle APB=PB \cdot PC \cdot \cos \angle BPC$

$m \cdot PA \cos \angle APB=PC \cdot \cos \angle BPC$

$題意より \ \ m \cdot AP=CP \ \ だから \quad \cos \angle APB=\cos \angle BPC$

$0 < \angle APB < \pi ,\quad 0 < \angle BPC < \pi \quad だから$

$\angle APB =\angle BPC $


$(別解)$

　

$AP:CP=1:m \quad より \quad PA:PC=1:m$

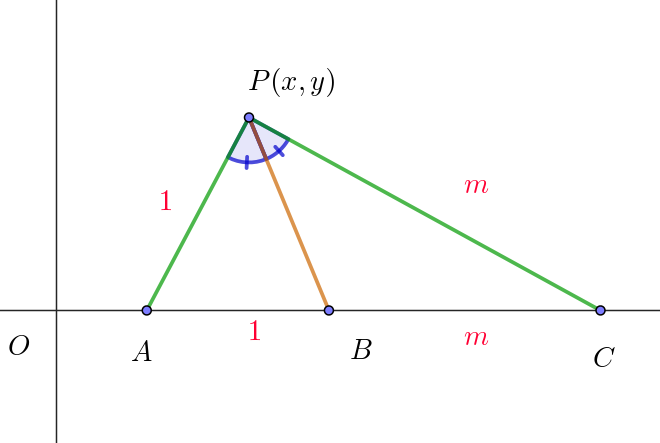
$また$

$AB:BC=(m-1):(m^2-m)=(m-1):m(m-1)=1:m$

$よって \quad \triangle PAC \ \ において \quad PA:PC=AB:BC \ \ が成りたつ$

$から \ \ PB \ は \ \ \angle APC \ \ の二等分線である。$

$このことについては($三角帰依の内角・外角の二等分線の性質$)をご覧ください。$


ページの先頭へ↑



メインメニュー　に戻る