金沢大学(理系) 2020年 問題4
$-2\pi \leqq x \leqq \pi\ \ のとき、関数 \ f(x)=\cfrac{2\sqrt{2}\pi}{3}(\cfrac{\sqrt{3}}{2}\sin \cfrac{x}{3}+\cfrac{1}{2}\cos \cfrac{x}{3})+\cfrac{(3-2\sqrt{2})\pi}{3}\ \ を考える。$
$次の問いに答えよ。必要であれば、\pi ^2 < 10 \ \ を用いてよい。$
$\qquad (1)\ \ f(x)\ は兵区間 \ [-2\pi,\ \pi]\ で増加することを示せ。$
$\qquad (2)\ \ 開区間 \ (-\pi,\ \pi)\ で、つねに \ \ f(x) > x \ \ が成り立つことを示せ。$
\[(3)\ \ f(x)\ の逆関数 \ f^{-1}(x)\ について、定積分 \ \ \int _{f(0)}^{f(\pi)} f^{-1}(x)dx \ \ の値を求めよ。\]
$\qquad (4)\ \ f(x)\ とその逆関数 \ f~{-1}(x)\ について、2つの曲線$
$\hspace{4em} C_1:y=f(x) \ \ (0 \leqq x \leqq \pi),\quad C_2:y=f^{-1}(x)\ \ (f(0) \leqq x \leqq f(\pi))$
$\hspace{3em} を考える。C_1,C_2\ および直線 \ x+y=f(0)\ \ で囲まれた図形の面積を求めよ。$
$(解説)$
$(1)\ \ f(x)の係数や定数項がきれいな値ではないのですが、逆にそれなりに計算しやすくできています。$
$(2)\ \ \pi ^2 < 10 をうまく用います。$
$(3)\ \ 逆関数には2通りの意味がありますが、(3)では本来の逆関数の定義がつかわれます。$
$\quad なお、三角関数の逆関数は大学の微積分で学びます。$
$(4)\ \ 逆関数のグラフ上の性質が使われます。(3)の計算結果も利用します。$
(1)
$f(x)=\cfrac{2\sqrt{2}\pi}{3}\sin (\cfrac{x}{3}+\cfrac{\pi}{6}) + \cfrac{(3-2\sqrt{2})\pi}{3}\ \ だから$
$f'(x)=\cfrac{2\sqrt{2}\pi}{3}\cos (\cfrac{x}{3}+\cfrac{\pi}{6}) \times \cfrac{1}{3}= \cfrac{2\sqrt{2}\pi}{9}\cos (\cfrac{x}{3}+\cfrac{\pi}{6}) $
$\qquad -2\pi \leqq x \leqq \pi より -\cfrac{\pi}{2} \leqq \cfrac{x}{3}+\cfrac{\pi}{6} \leqq \cfrac{\pi}{2}$
$よって \cos(\cfrac{x}{3}+\cfrac{\pi}{6}) \geqq 0 \quad より \quad f'(x) \geqq 0$
$ただし、f'(x)=0 \ \ となるのは \ \ \cfrac{x}{3}+\cfrac{\pi}{6} =\pm \cfrac{\pi}{2} \quad すなわち \quad x=-2\pi,\quad \pi \ \ のときだけである。$
$したがって \ \ f(x)\ はこの区間で単調増加となる。$
(2)
$g(x)=f(x)-x \quad とおくと$
$g(x)=\cfrac{2\sqrt{2}\pi}{3}\sin (\cfrac{x}{3}+\cfrac{\pi}{6}) +\cfrac{(3-2\sqrt{2})\pi}{3}-x$
$g'(x)=\cfrac{2\sqrt{2}\pi}{9}\cos (\cfrac{x}{3}+\cfrac{\pi}{6}) -1$
$ここで \quad \pi ^2 <10 \quad より \quad 8\pi ^2 <80 < 81 \quad 両辺の平方根をとって \quad 2\sqrt{2}\pi < 9 \quad \therefore \cfrac{2\sqrt{2}\pi}{9} < 1 $
$0 < \cfrac{2\sqrt{2}\pi}{9}\cos (\cfrac{x}{3}+\cfrac{\pi}{6}) \leqq \cfrac{2\sqrt{2}\pi}{9} <1 \quad だから \quad g'(x) < 0$
$g(x) > g(\pi)=\cfrac{2\sqrt{2}\pi}{3}\sin (\cfrac{\pi}{3}+\cfrac{\pi}{6}) +\cfrac{(3-2\sqrt{2})\pi}{3}-\pi= \cfrac{2\sqrt{2}\pi}{3} +\cfrac{(3-2\sqrt{2})\pi}{3}-\pi=0$
$よって \quad f(x) > x$
(3)
$y=f(x)\ の逆関数は \ x=f^{-1}(y)\ \ だから \quad (このことについては($逆関数$)を参考にしてください)$
\[I=\int _{f(0)}^{f(\pi)}f^{-1}(x)dx=\int _{f(0)}^{f(\pi)}f^{-1}(y)dy=\int _{f(0)}^{f(\pi)}xdy\]
$y=\cfrac{2\sqrt{2}\pi}{3}\sin (\cfrac{x}{3}+\cfrac{\pi}{6}) +\cfrac{(3-2\sqrt{2})\pi}{3} \quad より \quad dy=\cfrac{2\sqrt{2}\pi}{9}\cos (\cfrac{x}{3}+\cfrac{\pi}{6})dx$
\begin{eqnarray*} I &=&\int _0^{\pi}x\cfrac{2\sqrt{2}\pi}{9}\cos (\cfrac{x}{3}+\cfrac{\pi}{6})dx\\ \\ &=&\cfrac{2\sqrt{2}\pi}{9}\Big\{\big[3x\sin (\cfrac{x}{3}+\cfrac{\pi}{6})\big]_0^{\pi}- \int _0^{\pi}3\sin (\cfrac{x}{3}+\cfrac{\pi}{6})dx\Big\}\\ \\ &=&\cfrac{2\sqrt{2}\pi}{9}\Big\{3\pi- 3\int _0^{\pi}\sin (\cfrac{x}{3}+\cfrac{\pi}{6})dx\Big\}\\ \\ &=&\cfrac{2\sqrt{2}\pi}{3}\Big\{\pi+3\big[\cos (\cfrac{x}{3}+\cfrac{\pi}{6})\big]_0^{\pi}\Big\}\\ \\ &=&\cfrac{2\sqrt{2}\pi}{3}(\pi-3\times \cfrac{\sqrt{3}}{2})\\ \\ &=&\cfrac{2\sqrt{2}\pi^2}{3}-\sqrt{6} \pi\\ \end{eqnarray*}
(4)
$ポイントは2つです。$
(i)$\ \ y=f(x)\ のグラフと \ y=f^{-1}(x)\ のグラフは直線 \ y=x\ に関して線対称であること。$
(ii)$\ \ (2)より、f(x) > x \ \ だから \ \ f^{-1}(x) < x \ \ であること。$
$直線 \ \ x+y=f(0)\ \ は \ y=x\ に直交するから、この直線も \ y=x\ に関して対称である。$
$したがって$
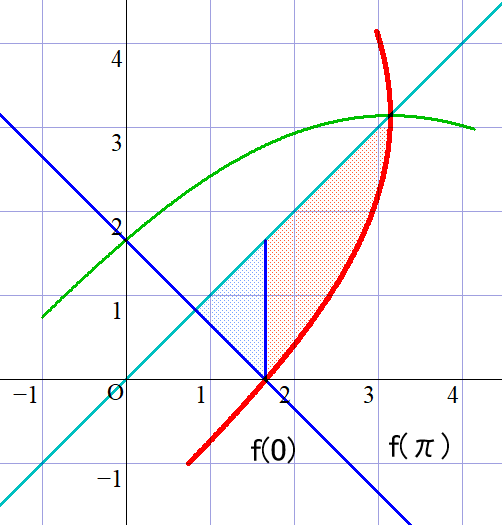
$C_1,\ C_2\ および \ 直線 \ x+y=f(0)\ \ で囲まれた図形Sの面積を同じくS、$
$直線 \ y=x,\ C_2\ および \ 直線 \ x+y=f(0)\ で囲まれた図形Tの面積を$
$同じくTとすると \quad S=2T$
$図形Tは、1辺 \ f(0)\ の正方形の\cfrac{1}{4}の三角形 \ T_1\ (右図の薄い青色部分)と$
$y=x\ と \ C_2\ とで挟まれた図形T_2(右図の薄い赤色部分)の和になる。$
$\qquad T_1=\cfrac{1}{4}f(0)^2$
\begin{eqnarray*}
T_2
&=&\int _{f(0)}^{f(\pi)}(x-f^{-1}(x))dx\\
\\
&=&\int _{f(0)}^{f(\pi)}xdx-\int _{f(0)}^{f(\pi)}f^{-1}(x)dx\\
\\
&=&\big[\cfrac{x^2}{2}\big] _{f(0)}^{f(\pi)} -\int _{f(0)}^{f(\pi)}f^{-1}(x)dx\\
\\
&=&\cfrac{1}{2}f(\pi)^2-\cfrac{1}{2}f(0)^2-\int _{f(0)}^{f(\pi)}f^{-1}(x)dx\\
\\
\end{eqnarray*}
\begin{eqnarray*}
T
&=&T_1+T_2\\
\\
&=&\cfrac{1}{4}f(0)^2+\cfrac{1}{2}f(\pi)^2-\cfrac{1}{2}f(0)^2-\int _{f(0)}^{f(\pi)}f^{-1}(x)dx\\
\\
&=&\cfrac{1}{2}f(\pi)^2-\cfrac{1}{4}f(0)^2-\int _{f(0)}^{f(\pi)}f^{-1}(x)dx\\
\\
&=&\cfrac{1}{2}\pi^2-\cfrac{1}{4}\big(\cfrac{3-\sqrt{2}}{3}\pi)^2 -(\cfrac{2\sqrt{2}\pi^2}{3}-\sqrt{6} \pi)\\
\\
&=&\cfrac{7-18\sqrt{2}}{36}\pi^2+\sqrt{6} \pi\\
\end{eqnarray*}
$したがって$
$S=2T=\cfrac{7-18\sqrt{2}}{18}\pi^2+2\sqrt{6} \pi$
メインメニュー に戻る