逆関数
1 逆関数の定義
$区間 \ [a,b]\ で連続な関数 \ f(x)\ が \ \ x_1 < x_2 \ \ (\ x_1,\ x_2 \in [a,\ b]\ \ )\ \ に対して$
(i)$\ \ f(x_1) < f(x_2) \ \ が成りたつとき、狭義の単調増加$
(ii)$\ \ f(x_1) > f(x_2)\ \ が成りたつとき、狭義の単調減少$
$といい、あわせて単調といいます。$
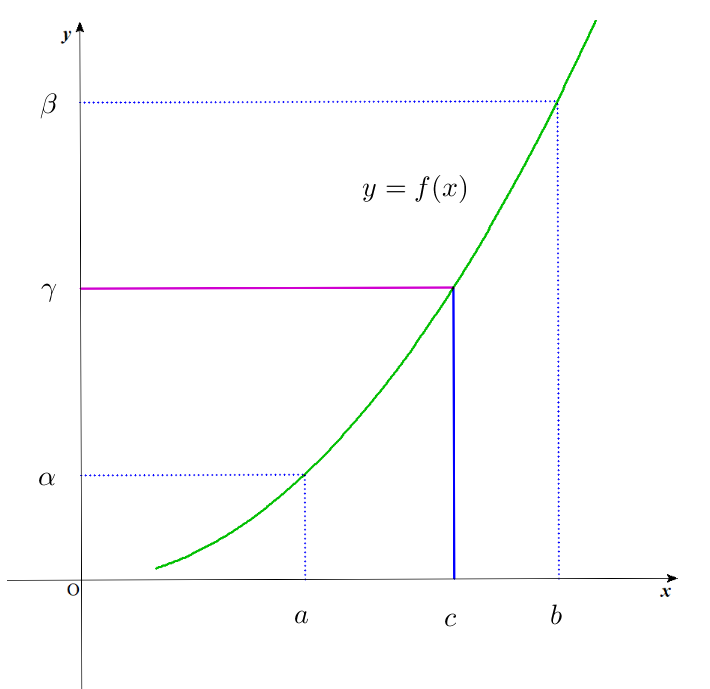
$関数f(x)が、区間 \ [a,\ b]\ で連続で単調のとき$
$\qquad f(a)=\alpha ,\quad f(b)=\beta \quad とする。$
$区間 \ [\alpha,\ \beta]\ の任意の\gamma に対して \ \ f(c)=\gamma \ \ となるようなcが$
$区間 \ [a,\ b]\ に1つあるので(これは中間値の定理です)$
$これを c=f^{-1}(\gamma)\ \ とかく。$
$一般に、x=f^{-1}(y)\ \ とかいて \ \ y=f(x)\ の逆関数といいます。$
$\qquad y=f(x) \quad \Longleftrightarrow \quad x=f^{-1}(y)$
$なお、y=f(x)\ の定義域を \ [a,\ b]、値域を \ [\alpha,\ \beta]\ とすると、$
$逆関数f^{-1}(x)\ の定義域は \ [\alpha ,\ \beta]、値域は \ [a,\ b]\ となります。$
$逆関数の導関数$
$\quad y=f(x)が区間 \ [a,\ b]\ で連続で、(a,\ b)\ で微分可能なとき、逆関数 \ x=f^{-1}(y)\ は微分可能で$
$\hspace{4em} \cfrac{dx}{dy}=\cfrac{1}{\dfrac{dy}{dx}}$
$微分法でよく使われる公式ですが、この逆関数はこちらの意味ですので注意してください。$
2 もう一つの逆関数
$関数については、習慣上独立変数をx,\ 従属変数をyとかくので、y=f(x)の逆関数 \ x=f^{-1}(y)\ について、$
$xとyを交換して \ \ y=f^{-1}(x)\ \ を逆関数という場合もあります。$
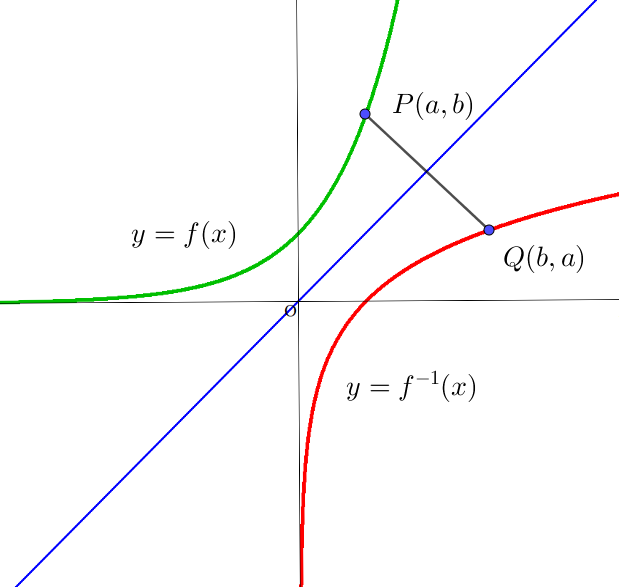
$y=f(x)\ のグラフと \ y=f^{-1}(x)\ のグラフにはきれいな位置関係があります。$
$y=f(x)上の点を \ P(a,\ b)\ とすると \ \ b=f(a) \quad よって \quad a=f^{-1}(b)$
$これは \ 点Q(b,\ a)\ が \ y=f^{-1}(x)\ 上にあることを示しています。$
$P(a,\ b)\ と \ Q(b,\ a)\ は直線 \ y=x\ に関して線対称ですから$
$一般に、y=f(x)\ のグラフと \ y=f^{-1}(x)\ のグラフは直線 \ y=x\ に関して$
$線対称となります。$
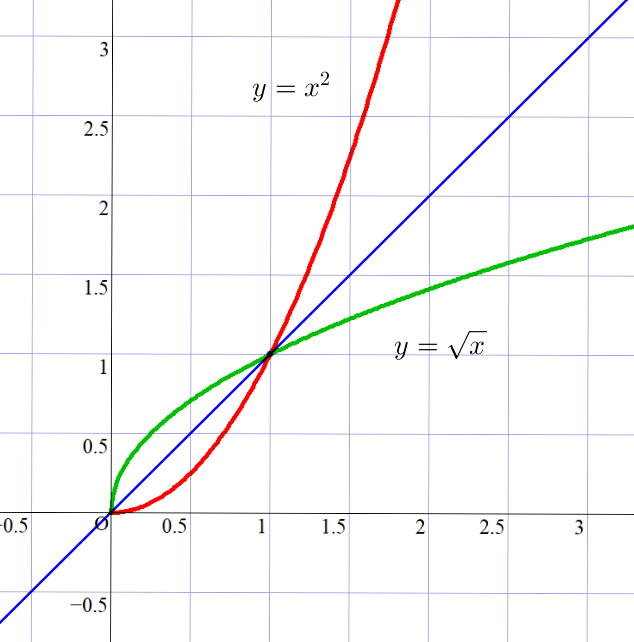
$例$
$y=x^2\ (x \geqq 0)\ と \ \ y=\sqrt{x},\quad y=e^x\ と \ \ y=\log x \ \ は互いに逆関数ですから$
$グラフは \ y=x\ に関して対称です。$
$y=\sin x \ の逆関数を \ y=\sin ^{-1}x \ \ (アークサインと読みます)\ とかきますが、$
$\sin x \ \ の(-1)乗ではありません。$
$他の三角関数も同様です。$
メインメニュー に戻る