条件付き確率
$例題1 くじ引き$
$当たりくじ3本を含む10本のくじから、1本ずつ2回引く。ただし、引いたくじは元に戻さない。$
$1本目引いたくじがはずれであったとき、2本目のくじが当たる確率は$
$2本目を引くじは、当たりくじ3本を含む9本のくじだから、これから1本引いたとき当たる確率だから$
$\hspace{3em} p=\cfrac{3}{9}=\cfrac{1}{3}$
$例題2 袋から玉を取り出す$
$赤玉3個、白玉5個が入った袋から1個ずつ2回玉を取り出す。ただし、取り出した玉は元に戻さない。$
$1回目取り出した玉が赤玉だったとき、2回目取り出す玉が白玉である確率は$
$2回目取り出す袋には、赤玉2個、白玉5個が入っているから、これから白玉を取り出す確率は$
$\hspace{3em} p=\cfrac{5}{7}$
$例題1と例題2のような確率を「条件付き確率」といいますが、これらの問題は非常にわかりやすい。$
$しかし、この説明で、条件付き確率はすべて言い尽くされたかというと、疑問です。$
$それは、確率の根本概念である、根元事象や全事象が全く明示されていないからです。$
$そこで、「条件付き確率」についてもう一度きちんと整理してみましょう。$

定義 条件付き確率とは
$標本空間(全事象)Sにおける2つの事象A,Bに対して、$
$事象 A \cap B, \ A \cap \overline{B},\ \overline{A} \cap B, \overline{A} \cap \overline{B} の4つの事象の要素の個数$
$(もちろん有限個です)が右表のとおりとします。$
$どの根元事象が選ばれるのも同様に確からしいとして$
$\cfrac{a}{a+b} を事象Aが起こったときの、事象Bが起こる条件付き確率といい、P_A(B)$ で表す。
$ところで、高校で勉強して以来ずっと気になっているのですが、「事象Aが起こった」という$
$ことは、「条件」なのでしょうか、$
$私には、事象Aが起こったという「情報」が得られたと思えてしかたないのです。$
$ですからこれは、「条件付き確率」でなく「情報付き確率」の方がしっくりくるのですが、どうでしょうか。$
$このことは、実際問題に当たると納得できると思います。$
$もっとも、この用語はしっかり根付いていますので、理解できればいいだけの話です。$
$本題にもどります。$
$同様にして他に、P_A(\overline{B}),\cdots ,P_{\overline{B}}(\overline{A}) の全部で8通りの条件付き確率が考えられます。$
$では、この定義を使って、次の問題を考えてみましょう。$
$例題3$
$1から10までの番号をつけた10枚のカードから1枚を取り出す。$
$取り出したカードの番号が奇数であった(という情報が得られた)とき、$
$その番号が3の倍数である確率は$
$取り出したカードの番号が奇数である事象をA、3の倍数である事象をBとする。$
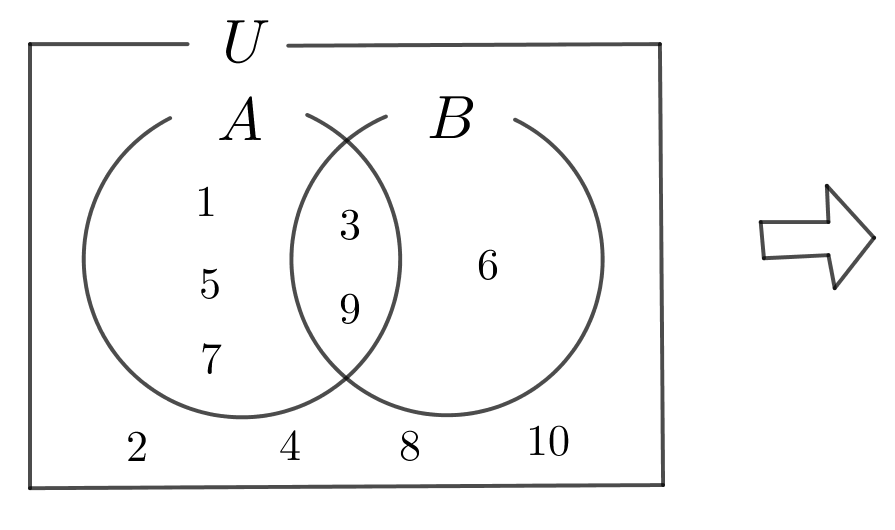
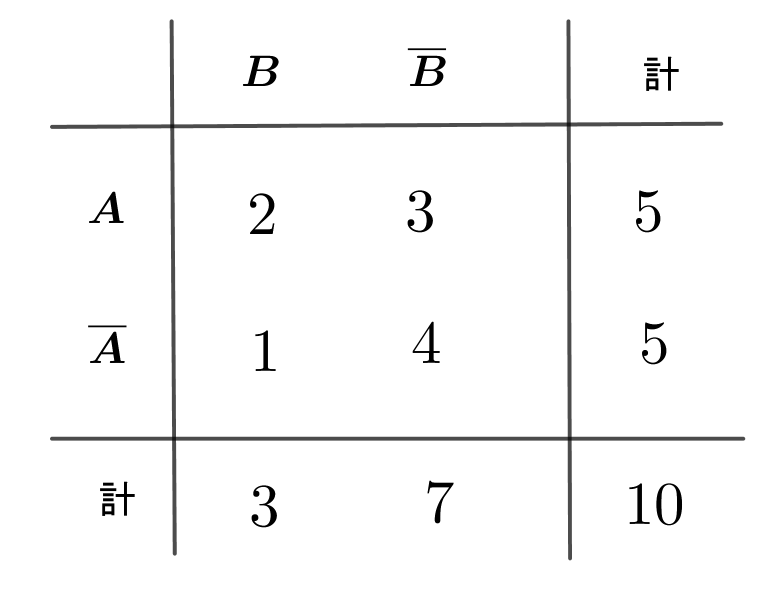
$条件付き確率の定義より \hspace{3em} P_A(B)=\cfrac{2}{5}$
$同様にして、取り出したカードの番号が3の倍数であったとき、その番号が奇数である確率は$
$\hspace{5em} P_B(A)=\cfrac{2}{3}$
$例題4$
$2つのさいころを投げたとき、出た目の和が偶数であることがわかった。$
$(このような情報が得られた)このとき目の和が8である確率は$
$目の和が偶数である事象をA、目の和が8である事象をBとすると$
$4つの事象の根元事象の要素の個数は下表のとおりです。$
$とくに\ \ B=\{(2,6),(3,5),(4,4),(5,3),(6,2)\}$
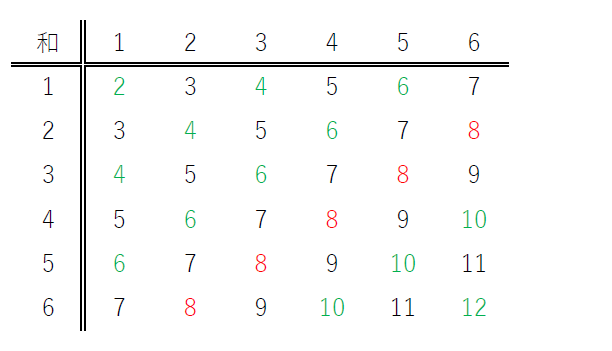
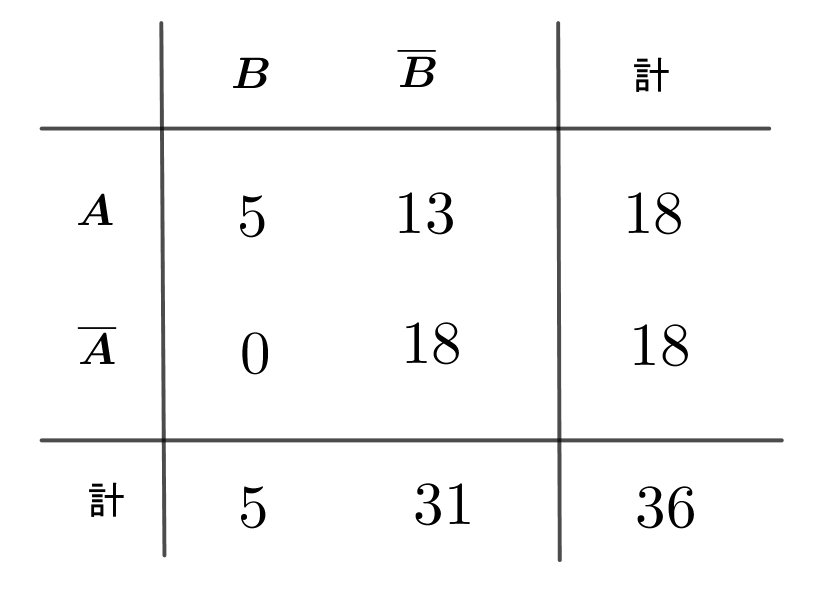
$したがって P_A(B)=\cfrac{5}{18}$
$ここで、例題1のくじ引きの問題を振り返りましょう。$
$くじに番号を付け、1,2,3は当たり、4~10ははずれとします。$
$1回目に引いたくじが当たる事象をA,2回目のくじが当たる事象をBとすると、全事象は下表のとおりです。$
$\hspace{3em} ○は可能な根元事象で、×は起こらない根元事象です。$
$\hspace{5em}$

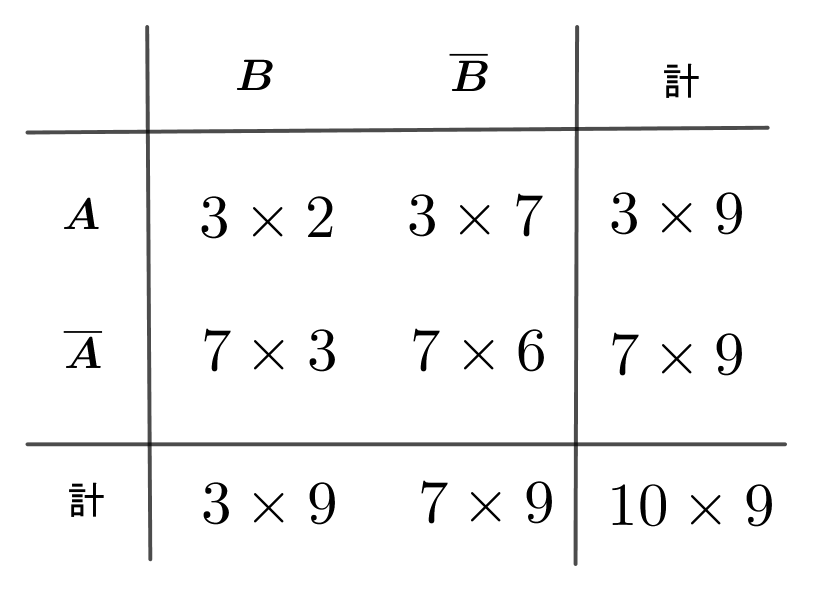
$\hspace{2em} P_{\overline{A}}(B)=\cfrac{7 \times 3}{7 \times 9}=\cfrac{1}{3}$
$これが定義から求めた条件付き確率です。$
$かなりやっかいですが、根元事象をきちんととらえた方法です。$
$この式を少し変形すると$
$\hspace{2em} P_{\overline{A}}(B)=\cfrac{7 \times 3}{7 \times 3 + 7 \times 6}=\cfrac{3}{3+6}$
$分母の 3+6 は くじが1本減って、あたり3本とはずれ6本があり、$
$分子の 3 は当たりが3本残っていることを表していますから、先に問題の内容$
$から直ちに求めた条件付き確率の値と一致していることが示されました。$
$例題2の袋から玉を取り出す問題も考えてみましょう。$
$赤玉3個をR_1,R_2,R_3とし、白玉5個をW_1,W_2,W_3,W_4,W_5とします。$
$1回目に赤玉が出る事象をA,2回目に赤玉が出る事象をBとすると全事象は下表のとおりです。$
$\hspace{3em} ○は可能な根元事象で、×は起こらない根元事象です。$
$\hspace{5em}$

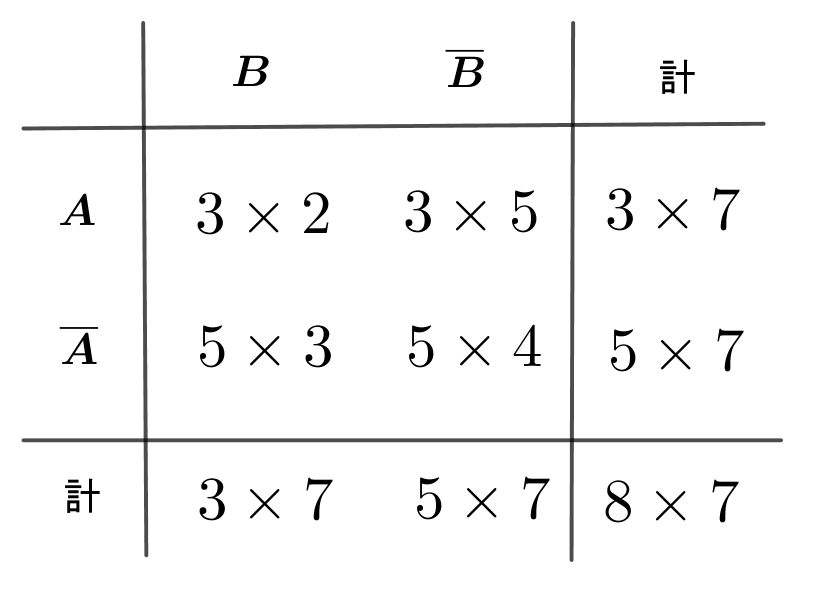
$まとめると右表のようになりますので$
$1回目に赤玉が出て,2回目に白玉が出る確率は$
$\hspace{2em} P_A(\overline{B})=\cfrac{3 \times 5}{3 \times 7}=\cfrac{5}{7}$
$これが定義から求めた条件付き確率ですが、$
$\hspace{2em} P_A(\overline{B})=\cfrac{3 \times 5}{3 \times 2 + 3 \times 5}=\cfrac{5}{2+5}$
$分母の 2+5 は 玉が1個減って、赤玉2個と白玉5個になり、分子の 5 は$
$白玉が5個残っていることを表していますから、先に問題の内容から直ちに$
$求めた条件付き確率の値と一致することが示されました。$
$最後に、条件付き確率の定理を紹介します。$
$P_A(B)=\cfrac{a}{a+b}=\cfrac{n(A \cap B)}{n(A)}=\cfrac{n(A \cap B)}{n} \times \cfrac{1}{\cfrac{n(A)}{n}}=\cfrac{P(A \cap B)}{P(A)}$
$n(A)は事象Aの根元事象の個数(集合Aの要素の個数)で、nはすべての根元事象の$
$個数(全事象の要素の個数)を表します。$
$普通これを使うことはありません。分母を払って$
$\hspace{3em}$ 乗法定理 $P(A \cap B)=P(A)P_A(B)$
$こちらの式が問題を解くときによく使われます。$メインメニュー に戻る