北海道大学(理系) 2020年 問題4
$\alpha を \ 0 < \alpha < 1\ を満たす実数とし、f(x)=\sin \cfrac{\pi x}{2} \ \ とする。数列\{a_n\}が$
$\qquad a_1=\alpha ,\quad a_{n+1}=f(a_n) \quad (n=1,2,\cdots )$
$で定義されるとき、次の問いに答えよ。$
$\hspace{2em}(1)\ \ すべての自然数nに対して、0 < a_n < 1 \ \ かつ \ \ a_{n+1} > a_n \ \ が成り立つことを示せ。$
$\hspace{2em}(2)\ \ b_n=\cfrac{1-a_{n+1}}{1-a_n}\ \ とおくとき、すべての自然数nに対して、b_{n+1} < b_n \ \ が成り立つことを示せ。$
\[(3)\ \ \lim _{n \rightarrow \infty } a_n \ \ および(2)で定めた\{b_n\}に対して \ \ \lim _{n \rightarrow \infty } b_n \ \ を求めよ。\]
$(解説)$
$(1)三角関数の漸化式はまず解けませんので、a_n をxとおいて微分法の力を借ります。$
$(2)は(1)の結果を利用するのかなと考えましたが、うまくいきません。やはり微分法に頼りましょう。$
$(3)がメインの問題です。単調数列が上限または下限に収束することは周知の事実ですが、$
$\hspace{1em} 大学の実数論で学ぶ内容です。$
(1)
$0 < a_n < 1 \ \ の証明は数学的帰納法で示します。$
(i)$\ \ n=1 \ \ のとき a_1=\alpha \ \ で \ \ 0 < \alpha < 1 \quad だから \quad 0 < a_1 < 1 $
(ii)$\ \ n=k \ のとき 0 < a_k < 1 \quad とすると$
$\hspace{3em} a_{k+1}=f(a_k)=\sin \cfrac{\pi a_k}{2}$
$\hspace{3em} 0 < \cfrac{\pi a_k}{2} <\cfrac{\pi}{2} \quad だから \quad 0 < \sin \cfrac{\pi a_k}{2} <1$
$よって \quad 0 < a_{k+1} < 1$
(i),(ii)$よりすべての自然数nに対して \quad 0 < a_n < 1 $
$a_{n+1} > a_n \quad の証明$
$\quad a_{n+1} - a_n =f(a_n)-a_n=\sin \cfrac{\pi a_n}{2}-a_n $
$\quad g(x)=\sin \cfrac{\pi x}{2}-x \quad (0 < x <1) \quad を考える。$
$\quad g'(x)=\cfrac{\pi}{2}\cos \cfrac{\pi x}{2}-1$
$\quad g''(x)=-(\cfrac{\pi}{2})^2\sin \cfrac{\pi x}{2} < 0 \quad だから \quad g'(x) \ は区間(0,1)で単調減少$
$\qquad g'(0)=\cfrac{\pi}{2}-1 > 0,\quad g'(1)=\cfrac{\pi}{2}\cos \cfrac{\pi}{2}-1=-1 < 0$
$\quad g'(x)は連続だから、中間値の定理より\ \ g'(\alpha)=0 \ \ となる \ \alpha \ が(0,1)に存在するが、$
$\quad g'(x)は単調減少だから \ \alpha \ は1つだけである。$

$\qquad g(0)=0,\quad g(1)=\sin \cfrac{\pi}{2}-1=0$
$増減表は$
\[
\begin{array}{c||c|c|c|c|c}
\hline
x& 0&\cdots& \alpha &\cdots& 1\\
\hline
g'(x)& & + & 0 & - & \\
\hline
g(x)&0 &\nearrow&極大&\searrow& 0\\
\hline
\end{array}
\]
$グラフは右図のとおり$
$\quad g(x) > 0 \quad だから \quad \sin \cfrac{\pi x}{2}> x \qquad \sin \cfrac{\pi a_n}{2}> a_n$
$\therefore \ \ f(a_n) > a_n \quad より \quad a_{n+1} > a_n $
(2)
$\quad b_n=\cfrac{1-a_{n+1}}{1-a_n}=\cfrac{1-\sin \cfrac{\pi a_n}{2}}{1-a_n} \quad だから \quad h(x)=\cfrac{1-\sin \cfrac{\pi x}{2}}{1-x} \ \ を考える。$
$\quad h'(x)=\cfrac{-\cfrac{\pi}{2}\cos \cfrac{\pi x}{2} \ (1-x)+(1-\sin \cfrac{\pi x}{2})}{(1-x)^2}$
$\quad h'(x)の分子を \ j(x) \ とおくと$
$\qquad j(x)=-\cfrac{\pi}{2}\cos \cfrac{\pi x}{2} \ (1-x)+(1-\sin \cfrac{\pi x}{2}) $
$区間(0,1) で考えると$
$\qquad j\ '(x)=(\cfrac{\pi}{2})^2\sin \cfrac{\pi x}{2} \ (1-x)+\cfrac{\pi}{2}\cos \cfrac{\pi x}{2} -\cfrac{\pi}{2} \cos \cfrac{\pi x}{2} =(\cfrac{\pi}{2})^2\sin \cfrac{\pi x}{2} \ (1-x)>0$
$よって \ \ j(x)\ \ はこの区間で単調増加 \quad j(1)=0 \quad だから \ \ 区間 \ (0,1)\ で \ \ j(x) < 0 $
$したがって \quad h'(x) < 0 \quad となり、h(x) は単調減少$
$(1) より \quad a_{n+1}> a_n \quad だから \quad h(a_{n+1}) < h(a_n)$
$ゆえに \quad b_{n+1} < b_n$
$また、b_n > 0 \ \ であることは定義式から明らかである。$
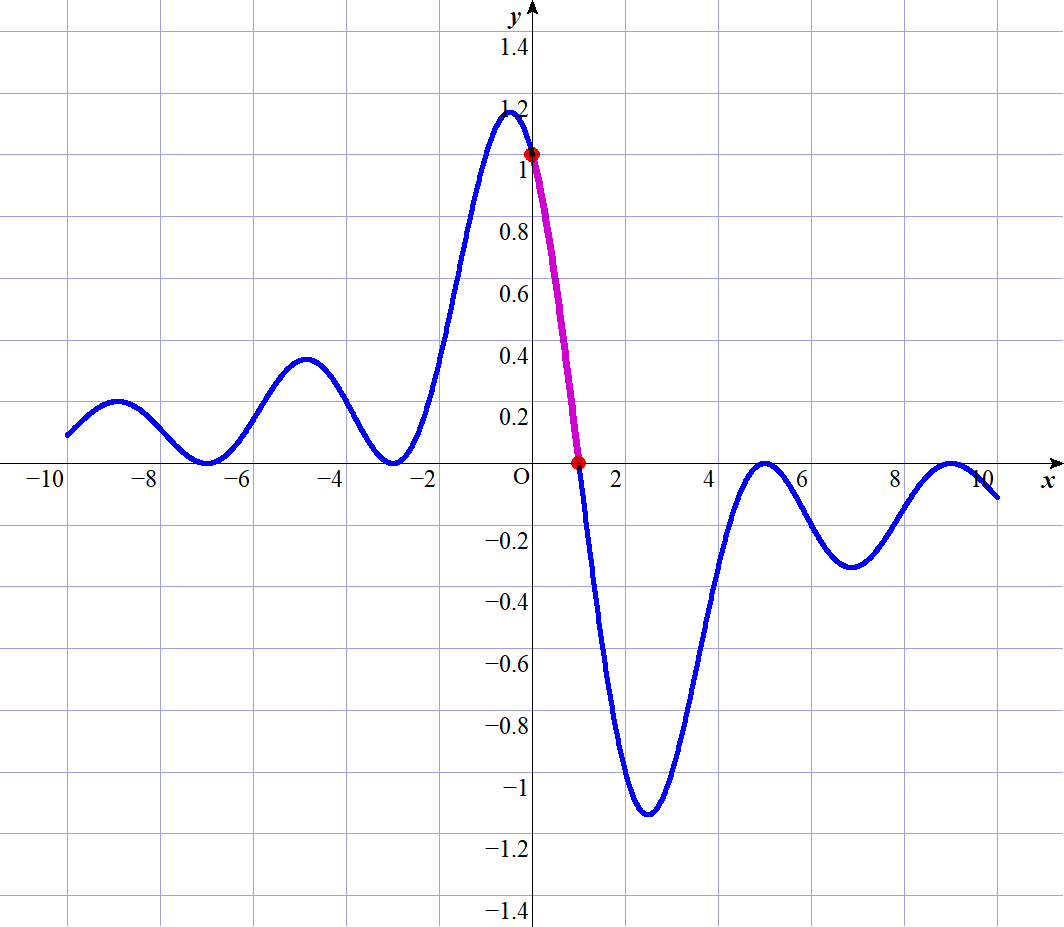
$しばらく寄り道をします。$
$h(x)\ は \ x=1\ では定義されていませんのあらためて$
$次のように定義しましょう。$
\[
\hspace{1em} h(x)=
\left\{ \begin{array}{l}
\cfrac{\small{1-\sin \cfrac{\pi x}{2}}}{1-x} \hspace{5em}(x \ne 1)\\
0 \hspace{9em}(x=1)\\
\end{array} \right.
\]
$このとき \ x=1 \ で連続かどうか調べます。$
$\quad 1-x=t \quad とおくと$
$h(x)=\cfrac{\small{1-\sin \cfrac{\pi x}{2}}}{1-x}=\cfrac{\small{1-\sin \cfrac{\pi}{2}(1-t)}}{t}
=\cfrac{\small{1-\cos \cfrac{\pi t}{2}}}{t}=\cfrac{\small{1-(1-2\sin ^2 \cfrac{\pi t}{4}})}{t}
=\cfrac{\pi^2}{8}t\Big(\cfrac{\small{\sin \cfrac{\pi t}{4}}}{\small{\cfrac{\pi t}{4}}}\Big)^2$
$\quad x \rightarrow 1 \quad のとき \quad t \rightarrow 0 \quad だから \quad h(x) \rightarrow 0$
$したがって h(x)\ は \ x=0 \ で連続であることがわかりました。$
$なお、右図はh(x)のグラフで、作成ソフトをつかって描いたものです。$
(3)
$\quad (1)\ \ より \quad a_1 < a_2 < \cdots < a_n < a_{n+1}< \cdots <1 \quad だから \quad a_n \rightarrow 1 \quad (n \rightarrow \infty)$
$\quad (2)\ \ より \quad 0 < \cdots < b_{n+1} < b_n < \cdots < b_2 < b_1 \quad だから \quad b_n \rightarrow 0 \quad (n \rightarrow \infty)$
$上に有界な単調増加数列と下に有界な単調減少数列がそれぞれ上限、下限に収束することは実数の$
$定義ですので、そのまま使ってもいいと思います。($単調数列の収束性$)を参考にしてください。$
$ただしこの解答で不安な人には次の解答でどうでしょうか。$
$\quad 0 < a_n < 1 \quad より \quad 1-a_n >0 $
$\quad b_n=\cfrac{1-a_{n+1}}{1-a_n} \quad より \quad b_n > 0 $
$\quad 1-a_{n+1}=b_n(1-a_n) < b_1(1-a_n) \quad だから$
$\quad 1-a_n < b_1(1-a_{n-1}) < b_1^2(1-a_{n-2}) < \cdots < b_1^{n-1}(1-a_1)$
$また$
$\quad a_1 < a_2 \quad だから \quad 1-a_1 > 1-a_2 > 0 \quad \therefore \cfrac{1-a_2}{1-a_1} <1 $
$\quad \cfrac{1-a_2}{1-a_1}=b_1 \quad だから \quad 0 < b_1 < 1 $
$\quad したがって \quad n \rightarrow \infty \quad のとき \quad b_1^{n-1} \rightarrow 0$
$挟打ちの原理より 1-a_n \rightarrow 0 \quad つまり \quad a_n \rightarrow 1 \quad (n \rightarrow \infty)$
$また$
$\quad f(1)=\sin \cfrac{\pi}{2}=1 \quad だから$
$\quad \cfrac{1-f(x)}{1-x}=\cfrac{f(1)-f(x)}{1-x} \longrightarrow f'(1) \quad (x \rightarrow 1)$
$\quad f'(x)=\cfrac{\pi}{2}\cos \cfrac{\pi x}{2}\quad より \quad f'(1)=\cfrac{\pi}{2}\cos \cfrac{\pi}{2}=0$
$よって \quad n \rightarrow \infty \quad のとき \quad a_n \rightarrow 1 \quad だから \quad \cfrac{1-f(a_n)}{1-a_n} \longrightarrow 0$
$ゆえに \quad b_n \rightarrow 0$
メインメニュー に戻る