正五角形の角と辺
1 辺と対角線のなす角
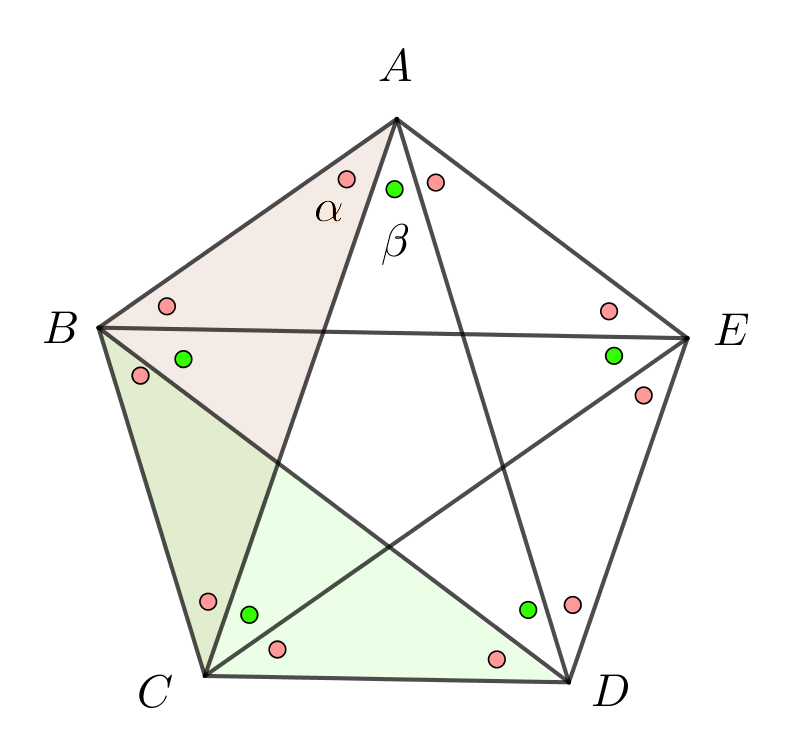
等しいことを示すのは案外やっかいです。
ここでは、2通りの方法で示します。
(方法1)
$△ABC と △BCD$ は $BA=CB,BC=CD,∠ABC=∠BCD$
2辺とその間の角が等しいので $△ABC \equiv △BCD$
また、$△ABC と △BCD$ はともに二等辺三角形だから
$∠BAC=∠BCA=∠CBD=∠CDB,AC=BD$
同様にして、右図の赤丸を付した角と対角線の長さはすべて等しい。
また
$△ACD と △CEA$ は3辺が等しいので $△ACD \equiv △CEA$
よって $∠CAD=∠ECA$
同様にして、右図の緑丸を付した角はすべて等しい。
$∠BAC=\alpha,∠CAD=\beta とおくと$
$△ABCで 4\alpha + \beta=180°$
$△ACDで 2\alpha + 3\beta=180°$
これを解いて $\alpha=\beta=36°$
(方法2)
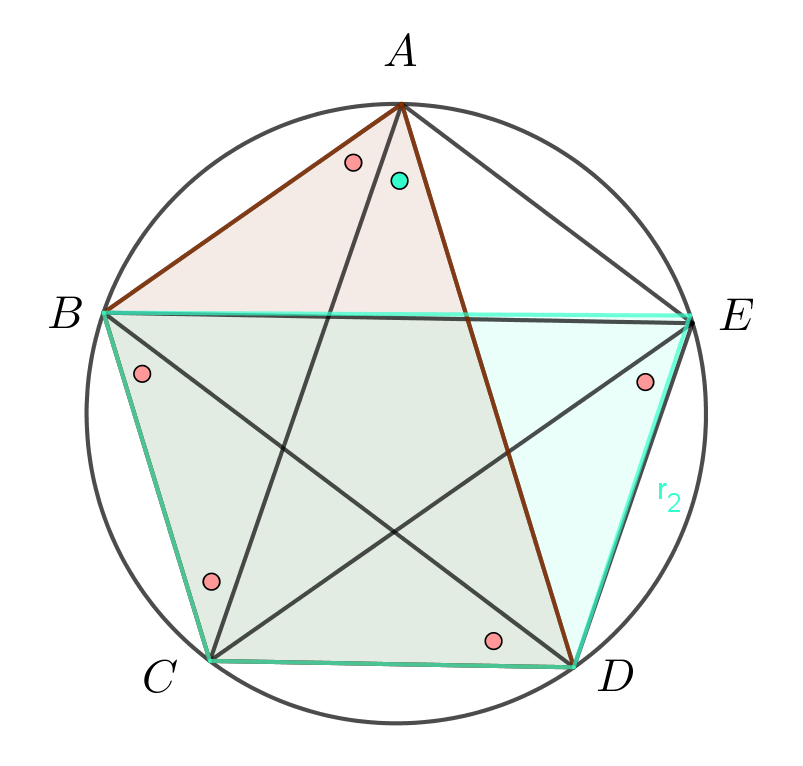
$∠BAC=∠CBD,∠BCA=∠CDB$
$△ABCは二等辺三角形だから ∠BAC=∠BCA$
同様にして、
右図の赤丸を付した角はすべて等しい。
$∠BAC=∠BDC$ だから円周角の定理の逆より
$4点A,B,C,Dは同一円周上にある。$
また
$∠CBD=∠CED$ だから円周角の定理の逆より
$4点B,C,D,E \ は同一円周上にある。$
$3点B,C.Dを通る円は1つに定まるから、5点A,B,C,D,E \ は同一円周上にある。$
また、同じ円で中心角(円周角)と弧の長さは比例するので、円周角が
等しい円弧の長さは等しい。
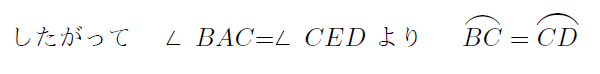
同じ長さの弧の上に立つ円周角は等しいので $∠BAC=∠CAD$
方法1は方程式を解くことからわかりやすいが、方法2は純粋に図形の性質
だけを用いて説明してあります。
2 対角線の長さ
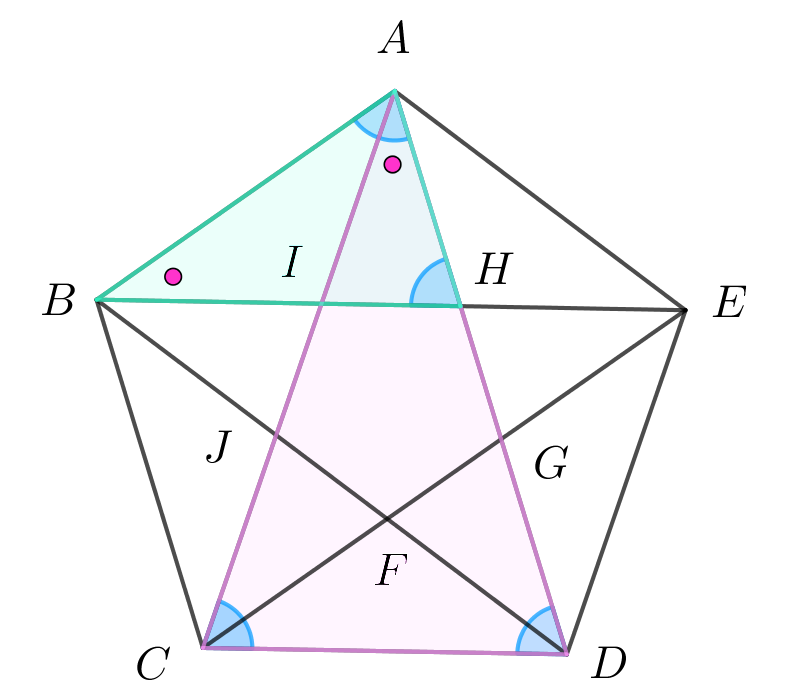
$∠BHA=∠EAH+∠AEH=2\alpha$
したがって
$∠BAH=∠BHA$ となり
△BAHは二等辺三角形である。
よって $BH=BA$
また $∠AIH=∠BAI+∠ABI=2\alpha$ だから
$∠AHI=∠AIH=2\alpha$ となり
△AIHは二等辺三角形である。
よって $AH=AI$
さらに $∠BIC=∠AIH=2\alpha$
$∠CBI=2\alpha$ だから
△CBIは二等辺三角形である。
よって $CI=CB$
次に
$△ACD と △BHA$において
$∠CAD=∠HBA,\ ∠ACD=∠BAH$
よって
$△ACD \sim △BHA$
$正五角形の1辺の長さをa,対角線ACの長さをbとすると$
$AH=AI=AC-CI=AC-CB=b-a$ だから
$AC:BA=CD:AH$
$b:a=a:(b-a)$
$b(b-a)=a^2$
$b^2-ab-a^2=0$
$\therefore \ b=\cfrac{1+\sqrt{5}}{2}a$
$なお、この \ \ \cfrac{1+\sqrt{5}}{2}\ \ は黄金数と呼ばれる値です。これについては($黄金数$)をご覧ください。$
3 小五角形の1辺の長さ

内角がすべて等しくなるから正五角形となる。
その一辺の長さは
\begin{eqnarray*} IH&=&BH-BI\\ &=&BA-AI\\ &=&BA-(AC-CI)\\ &=&BA-(AC-CB)\\ &=&2a-b\\ &=&2a-\cfrac{1+\sqrt{5}}{2}a\\
&=&\cfrac{3-\sqrt{5}}{2}a\\
\end{eqnarray*}
となります。
メインメニュー に戻る