黄金数
1 黄金数とは
$黄金比、黄金分割はもともとユークリッドの原論に由来するものです。$
$第 \ 6\ 巻の定義 \ 3\ に外中比として取り上げられています。$
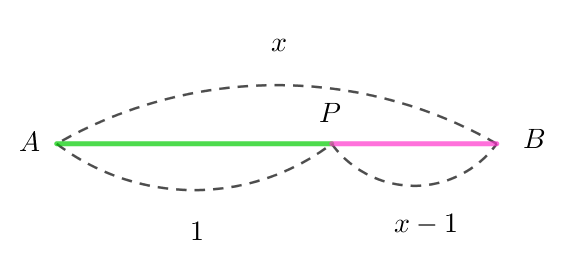
$線分 \ AB\ を \ AB:AP=AP:PB\ \ (ただし \ AP >PB)\ の比に分けることを$
$外中比に分けるといいます。$
$普通は全体を \ 1\ とおきますが、ここでは部分を \ 1\ とおきます。$
$\quad AP=1,\ \ AB=x \quad とおくと \quad x:1=1:(x-1) \qquad x(x-1)=1 \qquad \therefore \ \ x^2-x-1=0 $
$これを解いて \quad x=\cfrac{1+\sqrt{5}}{2}$
$現在は、この値を黄金数といい、\varphi \ \ であらわすと \quad \varphi=\cfrac{1+\sqrt{5}}{2}$
$他の解を \phi \ とおくと 解と係数の関係から \quad \varphi + \psi =1,\quad \varphi \psi=-1$
$なお、2辺の比 \ \ 1:\varphi \ \ は黄金比と言われています。$
2 黄金長方形
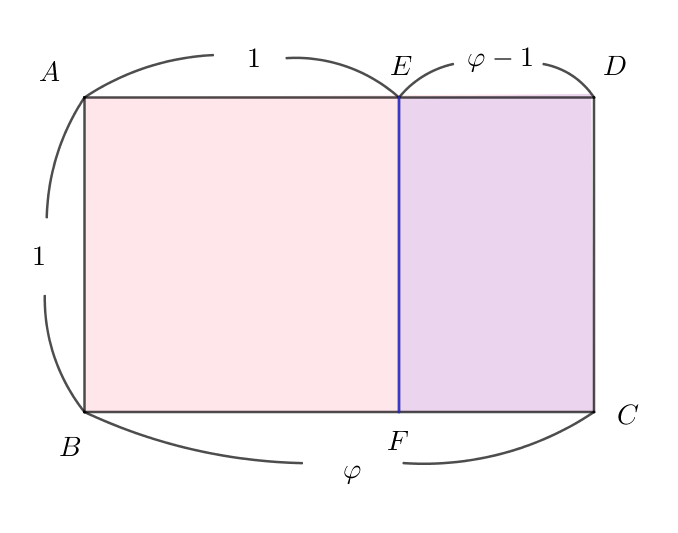
$右図のように \ 1,\ \varphi \ を \ 2\ 辺とする長方形を黄金長方形といいます。$
$この長方形 \ ABCD\ から \ 1\ 辺 \ 1\ の正方形ABFEを切り取った残りの$
$長方形 \ EFCD\ について$
$\quad DE : DC=(\varphi -1):1=(-\psi):1=1:(-\cfrac{1}{\psi})=1:\varphi$
$一般に \ 2\ 辺の長さの比が黄金比である長方形 \ EFCD\ も黄金長方形といいます。$
$さらに、この長方形\ EFCD\ から正方形を切り取った残りの長方形もまた黄金長方形となるのは同様です。$
$これが黄金長方形の特徴で、これゆえ最も美しく、調和のとれた長方形と言われています。$
3 黄金長方形の作図
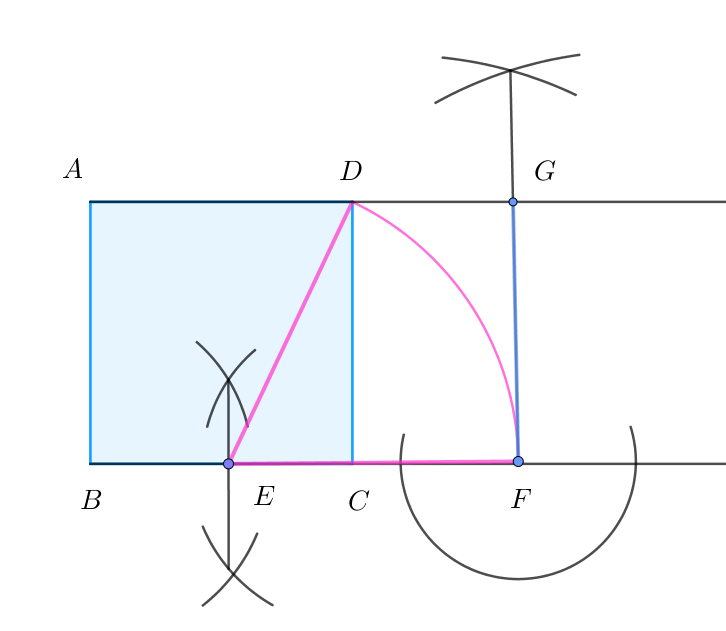
$1\ 辺 \ 1\ の正方形 \ ABCD\ をとり(作図方法は略)、辺 \ BC\ の中点を \ E\ とする。$
$直角三角形 \ CDE\ において、CD=1,\ \ CE=\cfrac{1}{2}\quad だから$
$\quad ED=\sqrt{1^2+\big(\cfrac{1}{2}\big)^2}=\cfrac{\sqrt{5}}{2}$
$BC\ の延長上に \ EF=ED\ となる点 \ F\ をとると$
$\quad BF=BE+EF=\cfrac{1}{2}+\cfrac{\sqrt{5}}{2}=\cfrac{1+\sqrt{5}}{2} \qquad これは黄金数である。$
$点 \ Fを通り、BF\ に垂直な直線と \ AD\ の延長との交点を \ G\ とすると四角形 \ ABFG\ は黄金四角形となる。$
4 cos 36°の黄金数表示
$\theta =36°=\cfrac{180°}{5}=\cfrac{\pi}{5} \qquad 5\theta =\pi \quad だから \quad 3\theta=\pi -2\theta $
$\sin 3\theta =\sin (\pi-2\theta) =\sin 2\theta \quad で \ 3\ 倍角、2\ 倍角の公式を用いて$
$3\sin \theta -4\sin ^3\theta=2\sin \theta \cos \theta \qquad \sin \theta \ne 0 \quad だから \quad \sin \theta \ で割って$
$3-4\sin ^2\theta =2\cos \theta \qquad 3-4(1-\cos ^2\theta) =2\cos \theta$
$4\cos ^2\theta -2\cos \theta-1=0 \qquad \cos \theta > 0 \quad だから \quad \cos \theta=\cfrac{1+\sqrt{5}}{4}$
$よって \quad \cos 36 °=\cfrac{\varphi}{2}$
5 黄金三角形
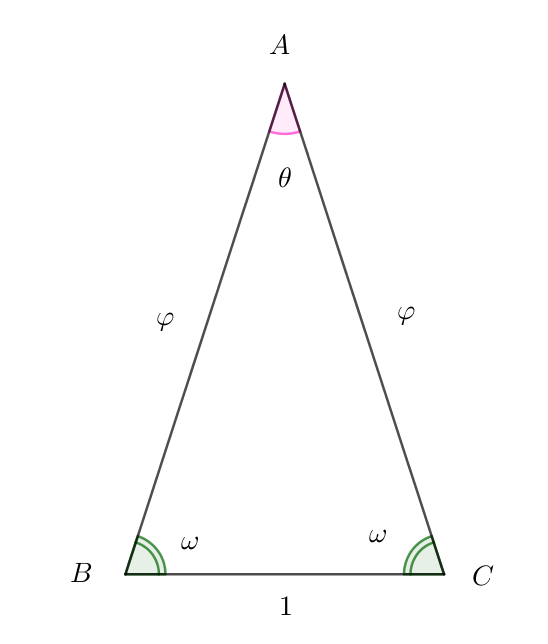
$右図のような底辺 \ 1,\ 等辺 \ \varphi \ の二等辺三角形 \ ABC\ について余弦定理より$
\begin{eqnarray*}
\cos \theta
&=&\cfrac{AB^2+AC^2-BC^2}{2AB\cdot AC}\\
&=&\cfrac{2\varphi^2-1}{2\varphi^2}\\
&=&1-\cfrac{1}{2}\cdot \cfrac{1}{\varphi^2}\\
&=&1-\cfrac{1}{2}\cdot \psi^2\\
&=&1-\cfrac{1}{2}(1-\varphi)^2\\
&=&\cfrac{1}{2}(1+2\varphi-\varphi^2)\\
&=&\cfrac{1}{2}(1+2\varphi-(\varphi +1))\\
&=&\cfrac{\varphi}{2}\\
\end{eqnarray*}
$4\ より \quad \cos 36 °=\cfrac{\varphi}{2} \quad だったから \quad \theta =36°$
$2\omega =180 °-\theta =180°-36°=144° \qquad \therefore \ \ \omega=72°$
$この二等辺三角形の \ 2\ 辺の比は黄金比になるから、黄金三角形といいます。$
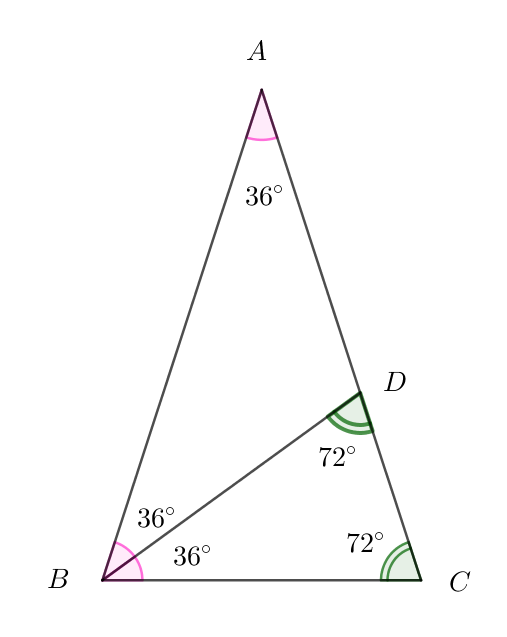
$\angle B \ \ の二等分線と辺 \ AC\ の交点を \ D\ とおくと$
$\angle BDC=180°-36°-72°=72°\quad となるから \quad \triangle BCD \sim \triangle ABC$
$したがって \quad BC:CD=AB:BC=\varphi : 1 \ \ となり$
$\triangle BCD \ は、また黄金三角形となります。$
6 正五角形と黄金比
$正五角形にも \ 36°、72°の三角形があらわれますが、これについては($正五角形の角と辺$)をご覧ください。$
メインメニュー に戻る