4　ガロア群と不変体


$\quad 定義　多項式　f(x) = (x-u_1)(x-u_2) \cdots (x-u_n) 　により体 \ F \ 上の分解体$
$\hspace{3em} （根体）が生成されるとき、F \ 上の \ K \ の自己同型群を方程式 \ f(x)=0 　の$
$\hspace{3em} ガロア群　あるいは \ F上 \ K \ のガロア群という。$


$\quad 定理6 \quad f(x)=0 \ がk個の相異なる解 \ u_1, \ u_2, \cdots , \ u_k \ をもつとき、定理2により、$
$\hspace{4em} 自己同型写像は、これらを互いに共役な解に写すから、ガロア群は相異なる$
$\hspace{4em} 解の置換そのものである。$


$方程式 x^4-4=0 \ を例にガロア群を考えてみましょう。$

(1) 分解体と自己同型写像



$\hspace{2em} x^4-4=0 　の解は　 (x^2-2)(x^2+2)=0 　より　x=\pm \sqrt{2},\ \pm \sqrt{2}i$

$\hspace{2em} 分解体は　K=Q(\sqrt{2},\sqrt{2}i)=Q(\sqrt{2},i) 　です。$

(i)$\quad Q \longrightarrow Q(\sqrt{2}) 　の拡大での自己同型写像は$

$\hspace{3em} \sqrt{2} \longrightarrow \sqrt{2} \ , \hspace{2em} \sqrt{2} \longrightarrow -\sqrt{2} 　　の2つ$

(ii)$\quad Q \longrightarrow Q(i) 　の拡大での自己同型写像は$

$\hspace{3em} i \longrightarrow i \ , \hspace{2em} i \longrightarrow -i 　　の2つ$

したがって　 $Q \longrightarrow Q(\sqrt{2},\sqrt{2}i)$ 　の拡大での自己同型写像は

$\hspace{1em}$ 　
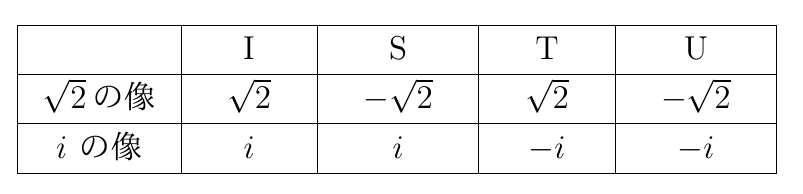
の4つあるが、$U=ST$ となることはすぐわかります。

したがって、ガロア群は　 $\{I,S,T,ST \}$です。

なお、$S^2=I,T^2=I,(ST)^2=I$ であるから、これは四元群に同型です。


(2) 不変体



$\quad KはQ上4次だから、4つの元 \{1,\ \sqrt{2},\ i,\ \sqrt{2}i\} からなる基底をもち、有理数係数の一次結合として$

$\hspace{5em} \xi=a+b\sqrt{2}+ci+d\sqrt{2}i 　　と表される。$

(i)$\quad S$による像

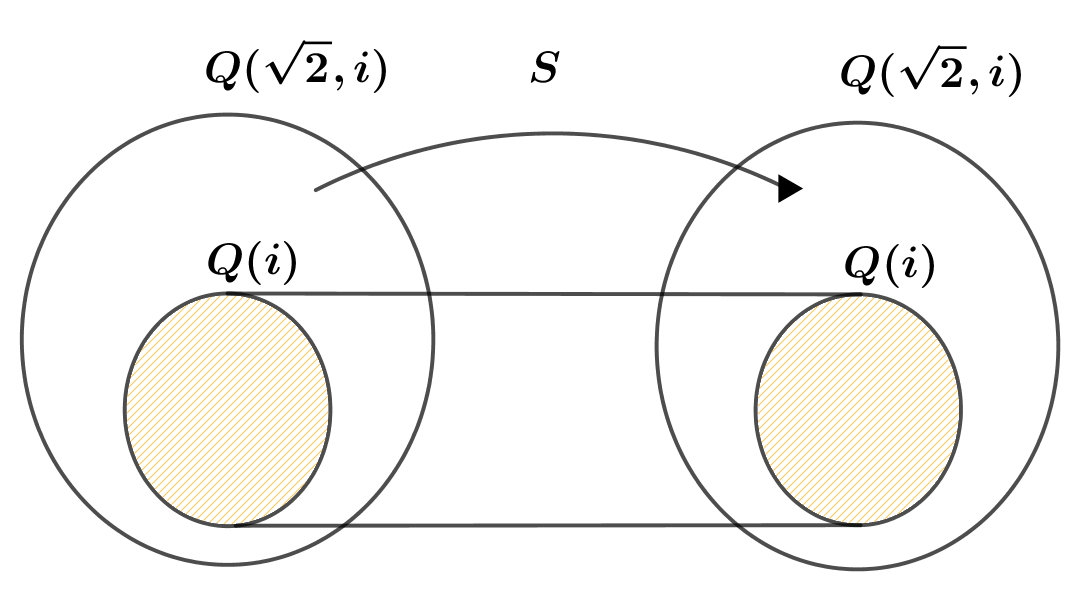
$\hspace{3em} \xi S=aS+b\sqrt{2}S+ciS+d\sqrt{2}iS$
$\hspace{4em} =aS+b\sqrt{2}S+ciS+d(\sqrt{2}S)(iS)$
$\hspace{4em} =a-\sqrt{2}b+ci-d\sqrt{2}i$

$\quad よって Q(i)の元は \ S \ で不変であることがわかります。$


(ii)$\quad T$による像

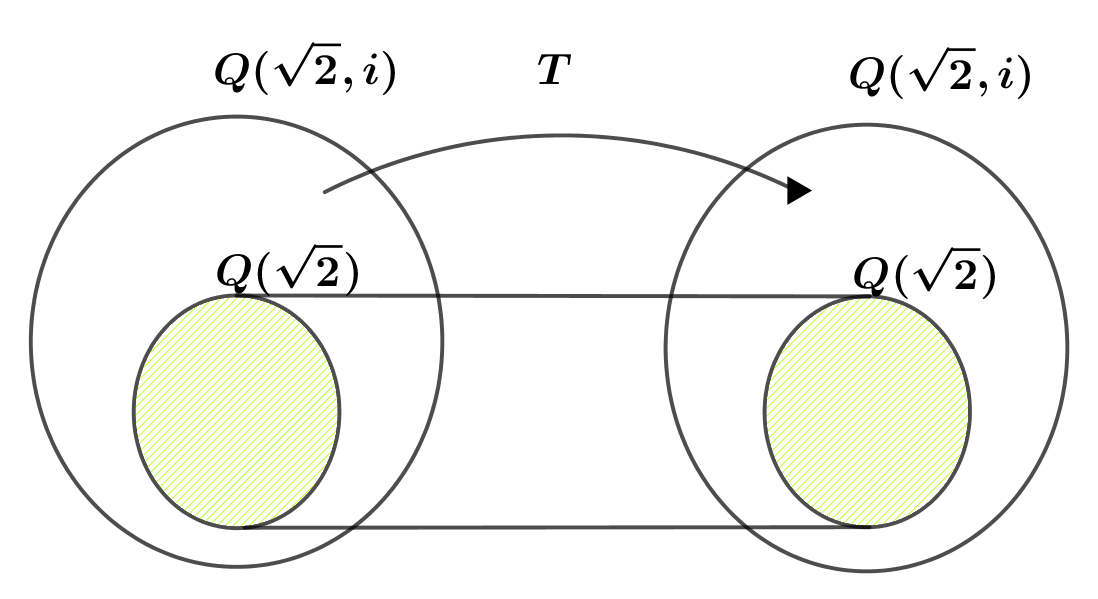
$\hspace{3em} \xi T=aT+b\sqrt{2}T+ciT+d\sqrt{2}iT $
$\hspace{4em} =a+\sqrt{2}b-ci-d\sqrt{2}i$

$\quad よって　 Q(\sqrt{2})の元は \ T \ で不変です。$



(iii)$\quad ST$による像

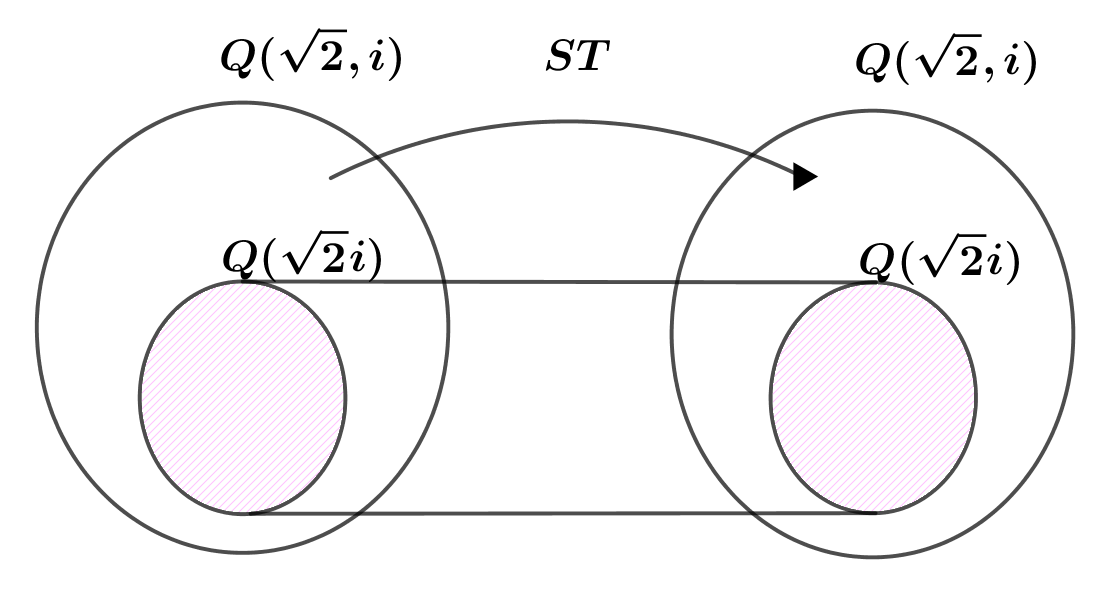
$\hspace{3em} \xi ST=aST+b\sqrt{2}ST+ciST+d\sqrt{2}iST $
$\hspace{4em} =a-b\sqrt{2}-ci+d\sqrt{2}i$

$\quad よって　 Q(\sqrt{2}i)の元は \ ST \ で不変です。$



$また、Gの部分群 M_1=\{I,S\},\ M_2=\{I,T\},\ M_3=\{I,ST\}$
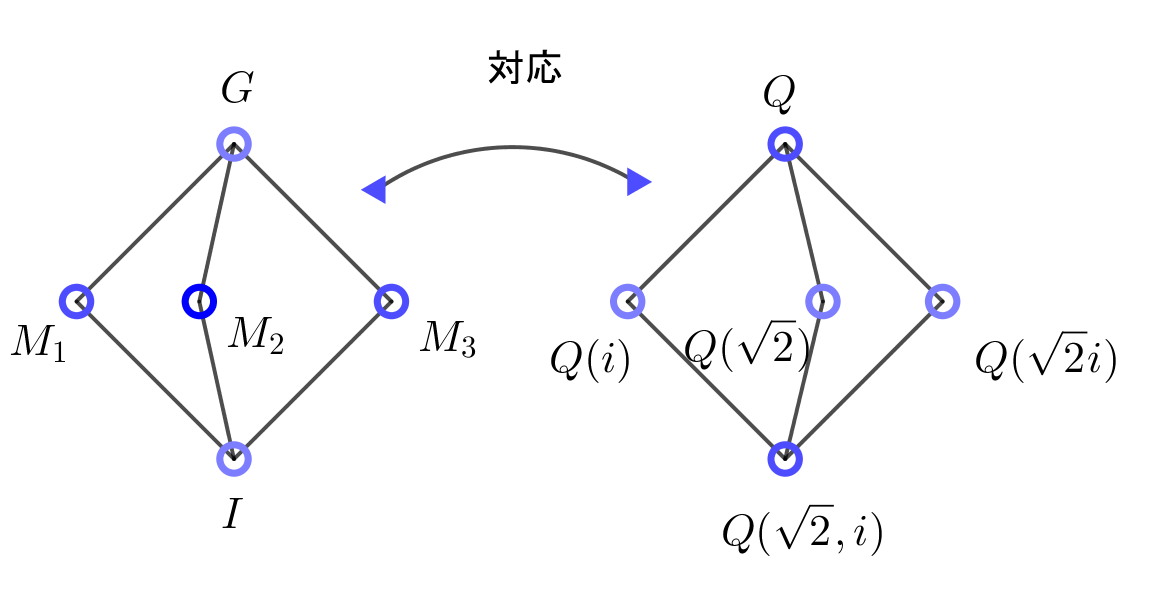
$と不変体との間に美しい対応がつけられます。$

$ハッセ図では右図のとおりです。$


(3) 置換による表現



$\hspace{2em} \sqrt{2} \longleftrightarrow 1 , \quad -\sqrt{2} \longleftrightarrow 2,\quad i \longleftrightarrow 3 ,\quad -i \longleftrightarrow 4$

のように対応づけると、ガロア群は解の置換そのものであるから

$\hspace{2em} S:\sqrt{2} \longleftrightarrow -\sqrt{2},\quad i \longleftrightarrow i \quad は \quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 2 & 1 & 3 & 4 \\ \end{array} \right) = \left( \begin{array}{r} 1 & 2 \\ \end{array} \right)$


$\hspace{2em} T:\sqrt{2} \longleftrightarrow \sqrt{2},\quad i \longleftrightarrow -i \quad は \quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 1 & 2 & 4 & 3 \\ \end{array} \right) = \left( \begin{array}{r} 3 & 4 \\ \end{array} \right)$


$\hspace{2em} ST:\sqrt{2} \longleftrightarrow -\sqrt{2},\quad i \longleftrightarrow -i \quad は \quad \left( \begin{array}{rr} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \\ \end{array} \right) = \left( \begin{array}{r} 1 & 2 \\ \end{array} \right) \left( \begin{array}{r} 3 & 4 \\ \end{array} \right)$


よって、ガロア群は

$\hspace{3em} G=\{e,\ (12),\ (34),\ (12)(34)\}$

とも表されます。



ページの先頭へ↑




ガロア群　に戻る


メインメニュー　に戻る