2 部分体$F$上の自己同型群
不変体
$\hspace{1em} 定理4 体 \ K \ の自己同型写像のうち、部分体 \ F \ のすべての元(要素)を不変にするものは$
$\hspace{4em} 群 \ G \ をなす。これを \ F \ 上 \ K \ の自己同型群という。$
$\hspace{5em}$ 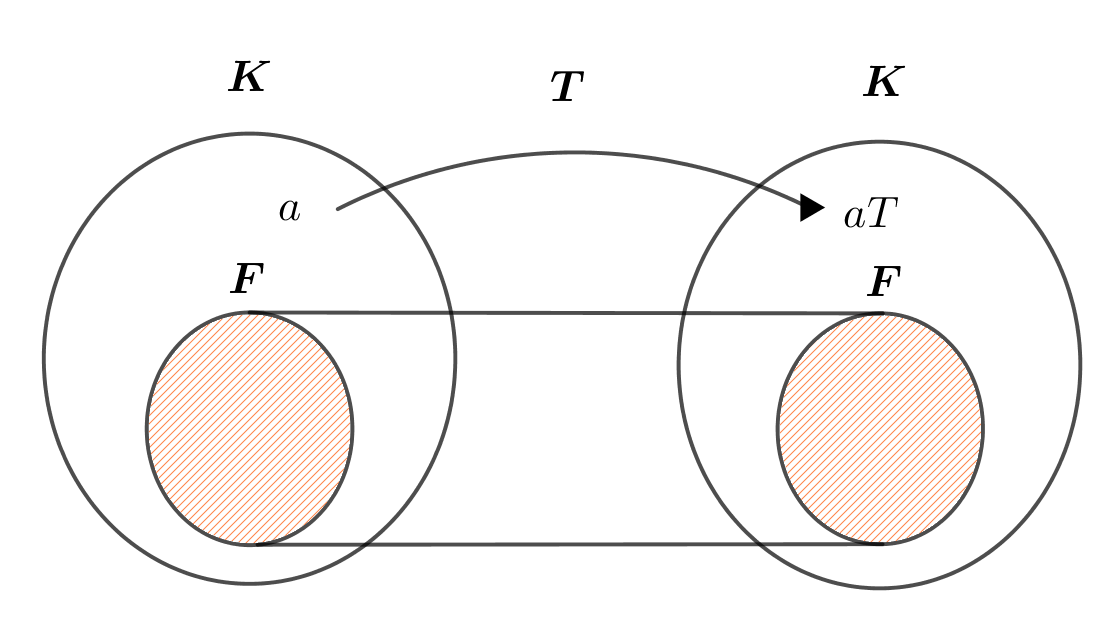
積について閉じていることを確かめれば十分である。
$\quad \forall b \in F, \quad T_1,T_2 \in G に対して$
$\quad b(T_1T_2)=(bT_1)T_2=bT_2=b$
よって $T_1T_2$ はFの元を不変にする。
$\hspace{2em} F \ を不変体、あるいは固定体といいいます。$
共役元
$\quad 体 \ K \ の元 \ u, \ v \ がともに \ F \ 上の同じ既約方程式 p(x)=0 の解であるとき、$
$\quad u \ と \ v \ は \ F \ 上で共役であるという。$
このとき、次の重要な定理が成りたつ。
$\hspace{2em} 定理5 F \ 上 \ K \ の自己同型写像 \ T \ は、K \ の各元 \ u \ をその共役元 \ \overline{u} \ に写す。$
(証明)
$\quad b_i \in F \quad i=0,1,\cdots , (n-1) とし、$
$\quad uをF上の既約方程式 p(x)=x^n+b_{n-1}x^{n-1}+ \cdots + b_0=0 \quad の解であるとすると$
$\quad u^n+b_{n-1}u^{n-1}+ \cdots + b_0=0$
これを$T$で写すと
$\quad (u^n+b_{n-1}u^{n-1}+ \cdots + b_0)T=0T$
$\quad u^nT+(b_{n-1}u^{n-1})T+ \cdots + b_0T=0T$
$\quad u^nT+(b_{n-1}T)(u^{n-1}T)+ \cdots + b_0T=0T$
$b_i \in F だから b_iT=b_i , \quad 0T=0 \ より$
$\quad (uT)^n+b_{n-1}(uT)^{n-1}+ \cdots + b_0=0$
$よって \quad uT= \overline{u} はまた p(x)=0 \ の解となるから、 \overline{u} \ は \ u \ と共役である。$
$例1 体 \ Q \ 上の拡大体 \ Q(\sqrt{2}) \ の自己同型群$
$\quad Q(\sqrt{2}) \ の要素 \ \sqrt{2}\ は \ Q \ 上の既約方程式 x^2-2=0 の解であり、$
$\quad 共役な解は \ \sqrt{2} と \ -\sqrt{2} \ である。よって自己同型写像は$
$\hspace{2em} I:\sqrt{2} \longrightarrow \sqrt{2}$ と $T:\sqrt{2} \longrightarrow -\sqrt{2}$
$\quad の2つがある。$
$\quad Q(\sqrt{2})の要素は a,b \in Q \ として a+b \sqrt{2} とあらわせるから$
\begin{eqnarray*} (a+b\sqrt{2})T &=&aT+(b\sqrt{2})T \hspace{22em}\\ &=&aT+(bT)(\sqrt{2}T)\\ &=&a+b(-\sqrt{2})\\ &=&a-b\sqrt{2}\\ \end{eqnarray*}
明らかに $T^2=I$ であり、自己同型群は $\{I,T\}$ である。
ガロア群 に戻る
メインメニュー に戻る